基于能控性和能观性的基础隔振装置的优化配置

王玉梅

（地震工程与工程振动重点实验室 中国地震局工程力学研究所，哈尔滨 150080）

近年来在结构振动控制方面发展了很多关于控制设备最优配置的方法。对于减隔震建筑，减隔震装置从广义上看，可以视为附加于原结构的被动激励或被动控制装置，于是其位置的最优化问题就成为控制器位置的最优化问题，最优控制就是用最小代价最大限度地把结构从一个状态转移到另一个预想的状态。在现代控制学领域，最优化问题有很多土木工程领域可以借鉴的思路，比如基于能控性和能观性概念的思路。能控性和能观性的概念多应用于航空器控制领域和电气自动化领域，作为自主导航和转换机反馈机制的控制［1－2］，它们描述了动态系统的输入 u（t）对状态 x（t）的控制能力和输出y（t）对状态x（t）的反应能力，恰与振动方程的状态空间表达式对系统的描述相对应。改变控制器位置即改变了输入的系数矩阵B，重塑了系统的动力性质，因此改变了系统的能控性。例如，如果控制器和传感器置于某振型的节点，即使控制器和传感器性能再优越，该位置也是既不能控也不能观的。通过建立能控性和能观性与振型的关系，就能建立相对振型的最优控制［3－5］，其中 Hamdan and Nayfeh的办法是在能控性和能观性的向量空间中引进一个广义角［5］；Choi等［6］改进了该方法，延伸到平衡坐标系统，并引进特征值的范数等衡量指标。

本文介绍的方法是由 Panossian等［7］提出并由Gawronski［8］完善的方法。这个方法把每个装备位置对特定振型的范数进行计算，然后按在系统模态参与的程度进行分级。它与LQR法的2－范数目标函数的控制目标相符。Silva等［9］采用了这个方法的H∞对他们的智能控制系统进行了控制器和传感器的选择。本文用既能反应能控性又能反应能观性，而且在线性变换中保持常数的Hankel奇异范数（Hankel singular norm，Hh）作为优化指数的判据基础。本文以基础减隔震建筑的隔振垫的布置为例，来说明这个方法在土木工程中的应用。

1 工程实例

这里以位于洛杉矶市的一幢八层RC建筑为例，研究最优控制。这是由美国ASCE学会下的控制委员会为方便土木工程界学者比较结构控制研究成果的应用，委托 Rice大学 Nagarajaiah等［10－11］以及 Erkus等［12］于2005年以洛杉矶市政厅为原型建立的数学模型，关于减隔震控制的Benchmark问题。该建筑总高35．1 m，总重2．031×105kN。1～6层平面为 L型，为82 m×54 m，7～8层为矩形，82 m×35 m。该问题定义了三种可选基础减隔震基础的数学模型和隔振垫的可选位置（92个），以及该结构的质量振型等参数，底层平面图如图1所示，每个位置点的坐标亦已知。结构的各层质量简化如表1所示。

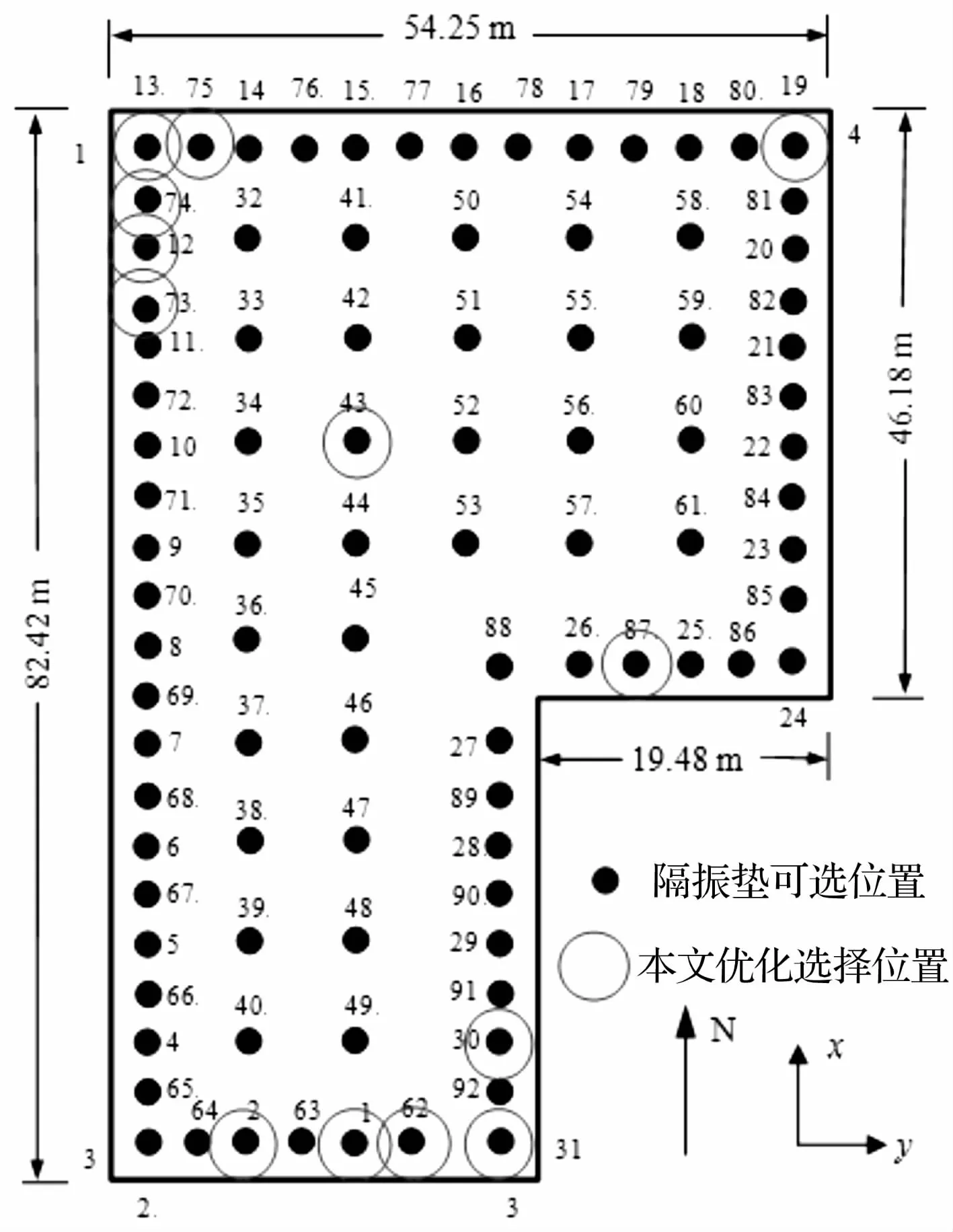
图1 底层平面图及隔振装置可选位置Fig．1 Base plan and available isolator locations

表1 楼层质量Tab．1 Story masses，（kN·s2·m－1）

加上基底底板和扭转效应，每层3个自由度，该建筑共27个自由度。原结构无隔振时x－，y－，r－方向的自振周期分别为 0．78 s，0．89 s，0．66 s。

经设计计算，取隔振垫总的等效刚度和阻尼系数为：kb＝2 119 kN／m，cb＝241．44 kN·s／m，对应平动和转动的隔振周期为2．28 s（x－），2．18 s（y－），及1．86 s（r－），等效阻尼比为 14．7% （x－），14．9%（y－），和17．9%（r－）［13］。设计要求，隔振剪力不应超过总结构总重量的10%。假设每个隔振垫水平承载力为1 500 kN，那么每个方向总数应不超过15个。

结构振动方程以状态空间方程表示：

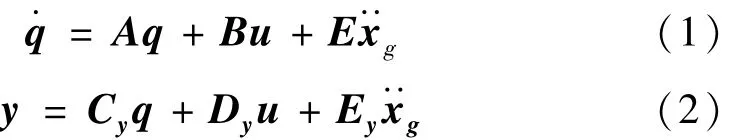
其中：q＝］为状态向量，y为输出向量，u为控制输入（这里为隔振控制），为地震动输入。z＝Φη，Z为上部结构相对于隔震层yb（下标b表示base）的位移。对于隔振结构，上部结构基本处于弹性状态，可以模态坐标η表示状态，与隔振层的常态坐标yb分开。这样做的好处是方便能控性和能观性的求解，但矩阵A、B、C包含相对于各层质心坐标的控制点和测量点的坐标转换矩阵，需要经过较复杂的坐标变换求得［10－13］。结构的质量、阻尼和刚度矩阵都为已知。控制器位置的信息包含在矩阵B中。传感器位置的信息包含在输出矩阵Cy中。

这里的控制器视为与隔振垫并列，控制输入即为隔振支座处的被动或主动力；传感器则与结构的输出并列，为反馈信号。

2 基本理论方法

能控性描述输入和状态的关系，涉及矩阵A和B的关系；能观性描述输出和状态的关系，涉及矩阵A和的Cy关系。线性时变系统能控和能观的判据是在时间区间［t0tf］内 Gram矩阵 grammians（Wc和 Wo）非奇异：

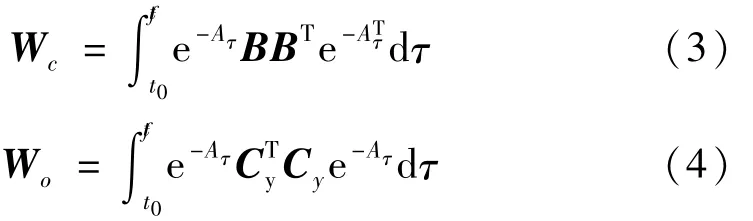
线性定常系统的判据是矩阵Wc和Wo为满秩，即：

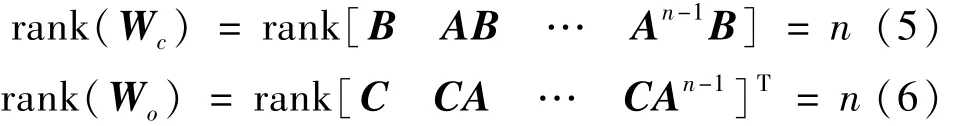
定常系统的Wc和Wo可以在Matlab中利用ctrb（）和obsv（）函数直接求出，从而判断系统的能控性和能观性。对于完全能控的线性定常系统，通过特别选定的坐标变换，可以将其状态方程化成标准的形式，称为能控规范形。当系统为不完全能控时，通过引入适当的坐标变换，可将它分解成能控的部分和不能控的部分。稳态系统的A，能控性和能观性的grammians都是正定的。

线性系统的解耦，要通过坐标变换x＝进行振型分解。土木工程领域较为熟知的第i振型的转换矩阵为：

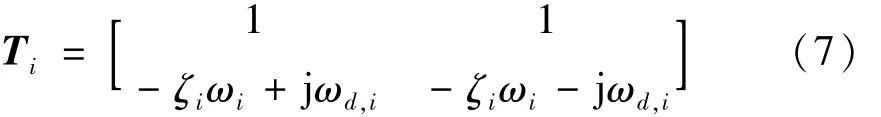
而控制领域较方便的是另一种解耦方式，即在上述转换矩阵的基础上乘以一个T′i，把矩阵A转换成实部和虚部分开的形式，其中

如此解耦的模态坐标系（AmBmCm）中（下标m表示模态坐标），grammians有下列性质［8－9］：

（1）近似对角阵，即

这里 wc，i和 Wo，i是模态能控性和能观性系数。

在对角阵中的对角项可表达为近似解析的解如下：

其示2－范数。

这个性质表明，在某种解耦的模态坐标系，不用计算行列式Am，grammian计算被大大简化了；同时也说明，第i个振型能控性近似与第i个输入的系数（矩阵）的平方成正比，第i个振型能观性近似与第i个输出的系数（矩阵）的平方成正比，它们都与第i个振型的阻尼和频率成反比。Hankel norm的值是两者的几何平均值，即

（2）令 G（ω）＝Cm（jωI－Am）－1Bm为模态坐标系统（AmBmCm）的传递函数（此式中的 j为虚部符号），则第i个模态的 Hankel norm恰为传递函数的模，即

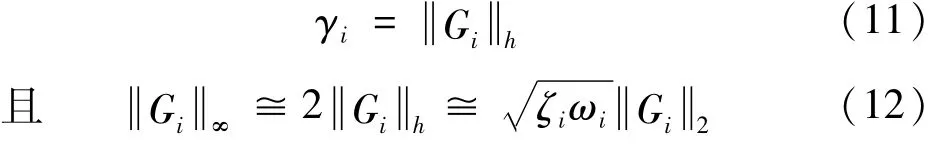
上述性质表明，把上部结构按 （7）、（8）解耦成（AmBmCm）的形式，不但可以使问题具有解析解的可能，还使与位置相关的能控性和能观性有了较清晰的物理意义：Hankel norm相当于传递函数峰值的二分之一。

只安装一个控制器或传感器的Hankel norm与安装s个控制器或r个传感器在第i模态（振型）的Han-kel norm的关系，是平方和均值（rms）关系，可以用下式表达［8］：

位置指数σij可以正则化评估第j个控制器在第i个模态（振型）的值，如式（14）所示：

上述位置指数可以很方便地排列成矩阵形式，如下所示：

位置指数矩阵可看出有两个着眼点：第一，可考察某个位置的控制器（传感器）对所有振型的重要程度，即从矩阵的列来看，其中第j项表示第j个控制器（传感器）对所有振型的位置指数：

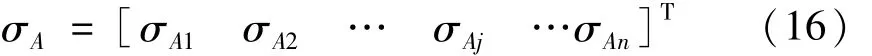
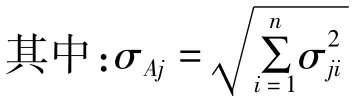
这个方法强调的是一个位置的整体重要性，而不强调其对某特定振型的作用，所以可能出现高振型导致的大的指数值。它不符合基础减隔震系统低频主导的设计目标，所以本文不考虑。

第二个角度，考察所有位置对一个振型的重要性，即从矩阵的行来看，是本文所关注的。其中第i项表示所有位置对第i个振型的位置指数：

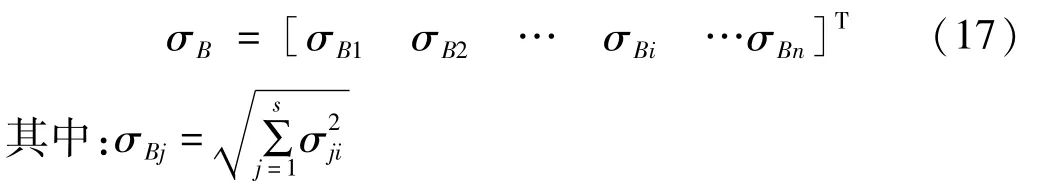
本文的位置指数以每个位置对低阶隔振振型（尤其第一振型）的贡献为关注重点，对应较小指数的位置将不设隔振垫。

当控制器或传感器有太多的位置可选时，重要性按指数值大小排序可能不够［8］。假设有一个位置有较大的指数值，那么与它很近的位置应该也会有较大的控制影响力，即较大的指数。最好是通过相关系数排除相关度高的位置［8］。首先定义一个基于第i个位置的、非正则化的Hankel范数的向量gi：

第i个位置和第k个位置的相关系数ρik定义为：

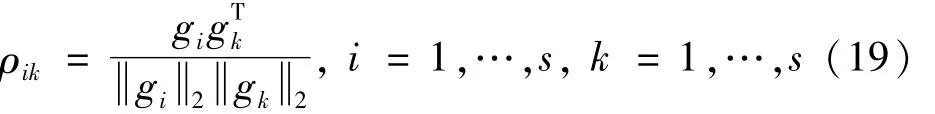
任给一个小的正数ε，例如ε＝0．001，定义一个选择指数 I（k）＝1，k＝1，…，s，其中 s是控制器（传感器）的个数，为：

如果I（k）＝1，那么第k个控制器（隔振垫）位置即被接受；如果I（k）＝0，那么第k个控制器（隔振垫）位置即被排除。对I（k）＝0，两个位置i和k或者高度相关（ρik＞1－ε），或者第 i个位置具有更高的 σi。

基于上述理论，求解最优位置的步骤如图2。

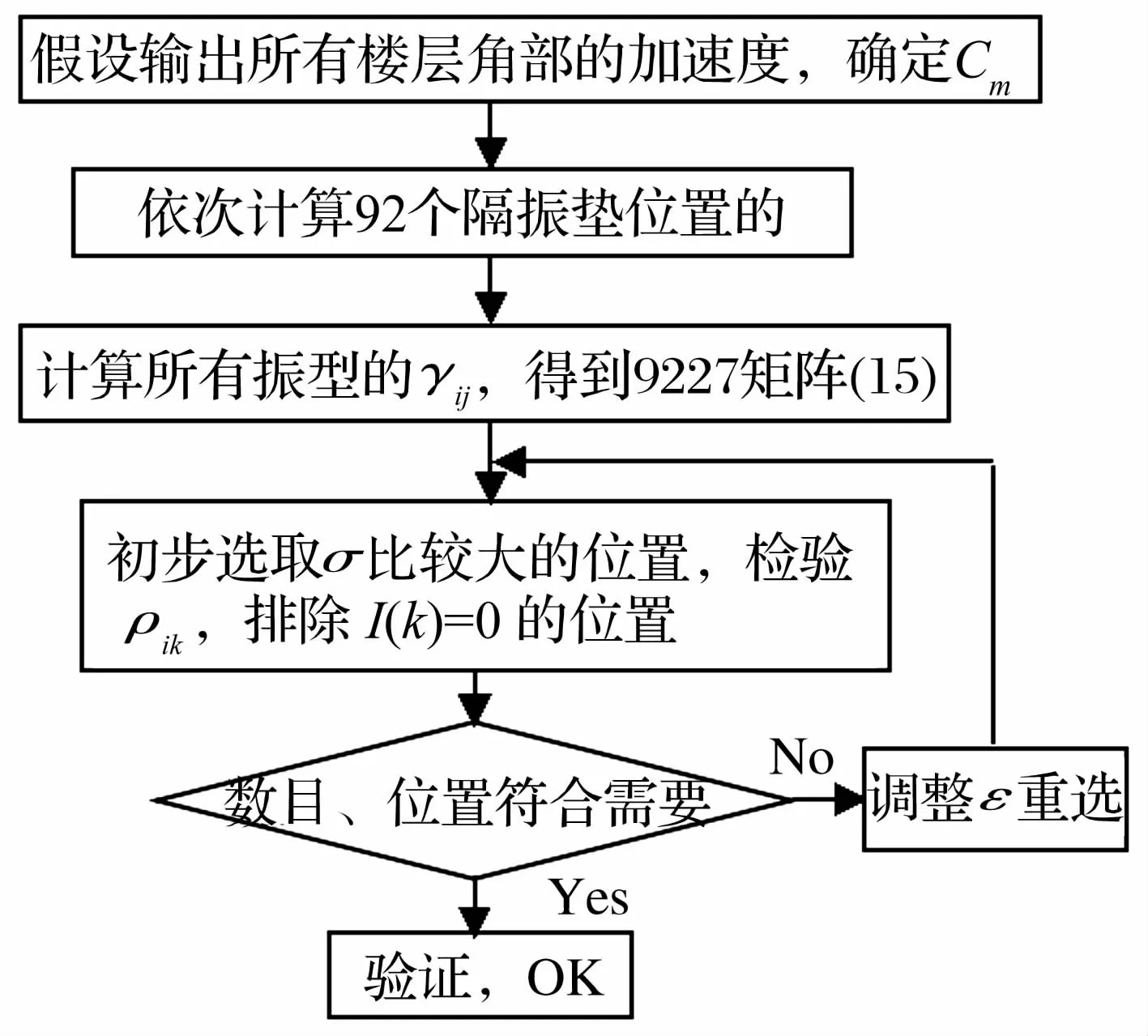
图2 最优隔振装置解题流程图Fig．2 Flow chart of optimal isolator location solution

3 计算与验证

计算表明，指数σij比较大的位置基本位于基础外围的角落附近和南部边缘，尤其靠近西南角（＃3）和东北角（＃19），这两点距质心最远，r－方向振型影响最大。图3为基于Hankel norm的位置指数计算图。横坐标为隔振垫位置编号，纵坐标为σij值。

图3（a）为1、2、3模态（x－，y－和 r－方向的第一振型）在 92个位置的数值，图 3（b）为 4、5、6模态（x－，y－和r－方向的第二振型）的。可见，指数较大的位置对上述6个振型基本一致，在x－，y－和r－方向有所不同。这些位置影响x－振型的位置是（＃1－3，31，60～65，90等）南面边缘处。影响y－方向的位置则不明显。原因是结构不规则，两个方向互相影响，但x－方向偏心更多。综合考虑各种可能情况和相关因素，下列位置（共22个）为初选结果：

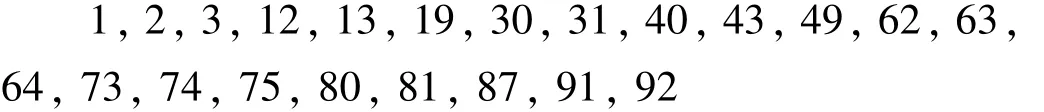
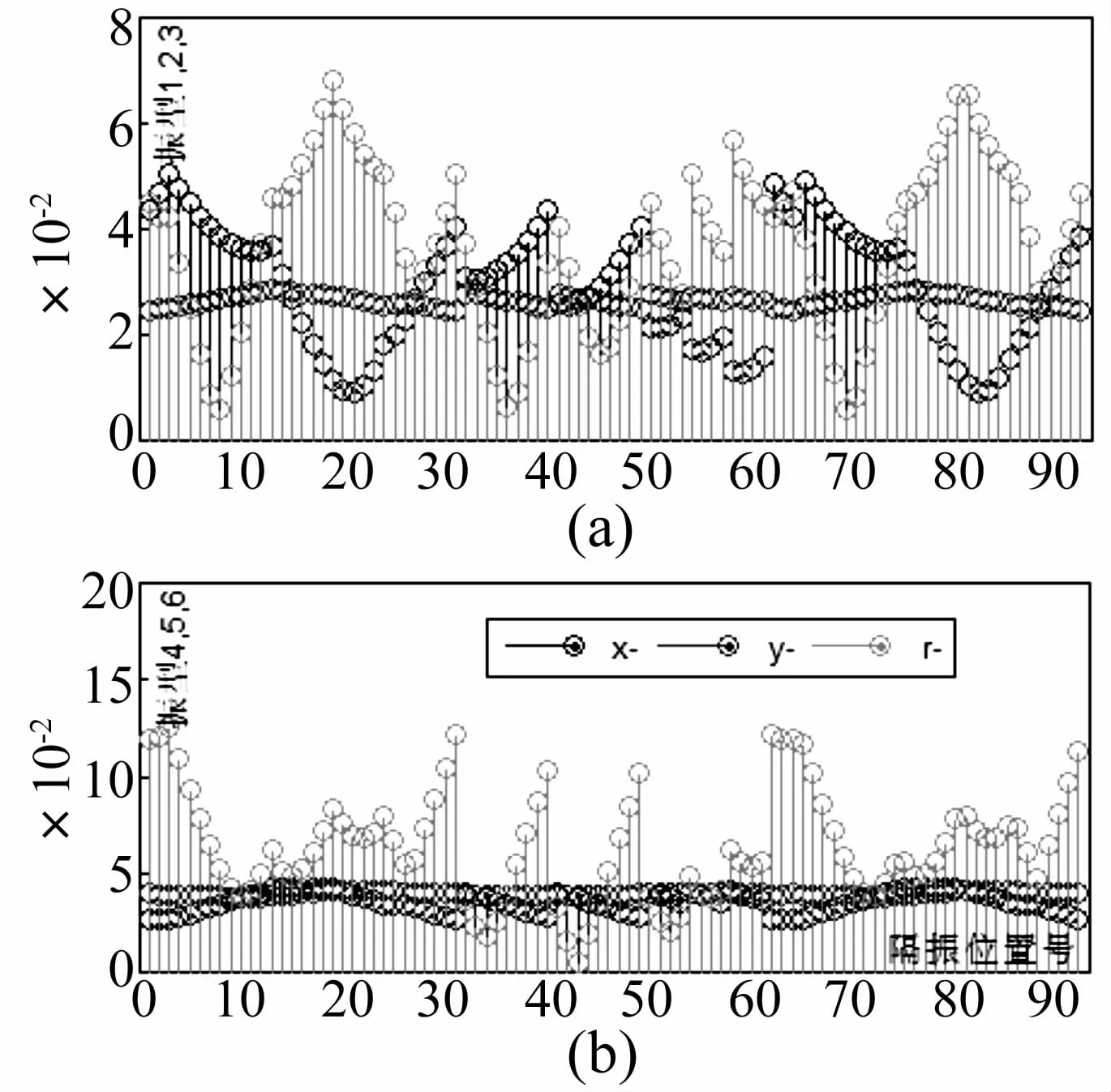
图3 隔振装置布置之Hankel norm指数Fig．3 Isolation device placement Hankel norm indices

假设ε＝0．001，对这22个选项进行相关性排除，排除I（k）＝0的7个左右就剩设计需要的15个。

根据表 2，位置 12，13，43，73，74，75，87，它们的I（k）＝1，是留下来的。表3总结了其余位置（第1列）及与其高度相关的位置（第2列，I（k）＝0）。两栏选一，即为彼此不相关度，或相关度较小，这些位置也将被保留。

从表3看出，3号、92号、63号、64号，91号出现频率高，说明与其它位置相关度高。删去它们，剩下17位置。但30号与40、49号相关度高，19号与80、81号相关度高，排除4个，剩13个，它们为：

1，2，12，13，19，30，31，43，62，73，74，75，87。这13个的布置图标注在图1中，以圆圈表示。

表3 隔振相关位置Tab．3 Correlated locations of isolators

剩下的13个比15个的目标少两个，由于初选的22个是按照σij的绝对值大小选的，样本少了点，也没有考虑凹角的两条边。根据观察，考虑平面布置，选取24号与88号附近的点，并把12号和13号换成长边的中部和下部的点，应该比较好，且能符合设计要求。但此次计算在初选范围和平面布置方面只做了上述选择，作为方法的实例应用。

另外，如图2流程图的最后一步，所得最优位置组合，需应用时程分析或其它方法，经过与其它组合进行比较，比较其对上部结构的抗震性能控制效果，来验证其为最优。但本研究尚未进行这方面的工作，将待日后逐步完善。

4 结 论

本文提出了一种可对基础减隔震装置位置选优的，基于能控性和能观性的方法，在控制理论应用于土木工程的最优化研究方面做了尝试和探索。该法通过模态坐标转换，计算结构状态方程的系数矩阵，以及Hankel奇异范数，来构造位置指数矩阵，并用相关性计算排除相关度高的位置，避免控制力重复施力而实现最优化。所提方法通过一个平面不规则的多层RC工程实例进行了示范计算，所得结果符合工程经验判断，其可靠性需进一步研究。

［1］王晓明．基于能观能控理论的航天器自主导航与控制方法研究［D］．哈尔滨：哈尔滨工业大学，2009．

［2］胡宗波，张波，邓卫华，等．PWM DC－DC变换器混杂动态系统的能控性和能观性［J］．电工技术学报，2005，20（2）：76－82．HU Zong-bo， ZHANG Bo， DENG Wei-hua， et al．Controllability and observability of PWM DC－DC converters as hybrid dynamic systems［J］．Transactions of China Electrotechnical Society，2005，20（2）：76－82．

［3］Longman R W，Siilin S W，Li T，et al，The fundamental structure of the degree of observability［R］．AIAA／AAS，San Diego，1982：82－1434．

［4］Moore B C．Principle component analysis in linear systems：Controllability，Observability，and Model Reduction［J］．IEEE Transactions on Automatic Control，1981，26（1）：17－32．

［5］Hamdan A M A， Nayfeh A H． Measures of modal controllability and observability for first-and second-order linear systems［J］．Journal of Guidance，Control，and Dynamics，1989，12（3）：421－428．

［6］Choi J W，Park U S，Lee S B．Measures of modal controllability and observability in balanced coordinates for optimal placement of sensors and actuators：a flexible structure application［C］．Proceedings of SPIE，Smart Structures and Materials 2000：Mathematics and Control in Smart Structures，2000，3984：425－436．

［7］Panossian H，Gawronski W，Ossman J．Balanced shaker and sensor placement for modal testing of large flexible structures［C］．1998，IMAC－XVI，16th International Modal Analysis Conference-Model Updating ＆ Correlation， Santa Barbara，CA．

［8］Gawronski WK．Dynamics and control of structures：A Modal Approach［M］．1998，Springer－Verlag New York，Inc．

［9］Silva S，Lopes Jr V．Robust control to parametric uncertainties in smart structures using linear matrix inequalities［J］．Journal of the Brazil Society of Mechanical Science＆Engineering，2004（4）：430－437．

［10］ Narasimhan S，Nagarajaiah S，Johnson E A，et al．Smart base isolated benchmark building，part I：problem definition［J］．Journal of Structural Control and Health Monitoring，2005；DOI：10．1002／stc．99．

［11］Nagarajaiah S，Narasimhan S．Smart base isolated benchmark building part II：sample controllers for linear and friction isolation［J］．Journal of Structural Control and Health Monitoring， Published Online， 2005； DOI： 10．1002／stc．100．

［12］ Erkus B，Johnson E A．Smart base isolated benchmark building part III：a sample controller for bilinear isolation［J］． Journal of Structural Control and Health Monitoring2004；DOI：10．1002／stc．101．

［13］Wang Yu-mei．Control strategies for 3D smart base isolation systems using modal and nodal approaches［D］．Ph．D Dissertation，Washington University in St．Louis，2006．