基于EMD和神经网络的轮轨故障噪声诊断识别方法研究

江 航，尚春阳，高瑞鹏

（西安交通大学 机械工程学院，西安 710049）

由于我国人口众多，流动人口大，物资货运量大，在交通日益发达的今天，铁路运输依然是最主要的交通运输方式。随着列车高速、重载、高密度的运行，列车运行的安全性越来越受到人们的关注。铁路轮轨故障诊断经过各国科研工作者的努力已经拥有大量的方法［1－6］，但利用轮轨噪声信息进行故障诊断的研究还比较少。轮轨噪声作为列车运行的附带品，包含着相当多的列车和钢轨状态信息，对轮轨噪声进行采集分析能够实现对轮轨故障的诊断。

采用神经网络方法对故障进行分类识别，诊断过程最关键的问题之一是对各种故障特征参数的提取，它直接影响着故障分类识别的准确性与有效性。在信号分析中，时间尺度与时间尺度上的能量是常分析的对象。当列车车轮或轨道存在缺陷时，其产生的轮轨噪声信号在不同的时间尺度上能量分布就会发生变化，同时反映信号冲击成分的峭度指标也会产生变化。因此，提取轮轨噪声信号各时间尺度上的能量与峭度特征作为神经网络的特征参数输入，能够实现对轮轨故障的分类识别。

轮轨噪声信号是一种非平稳信号，小波包分析方法能够将其分解到不同的时间尺度上，并且可以同时实现较高时间分辨率和频率分辨率，其各频带的能量特征能反映故障的信息［7］。但是小波包分析方法是预先选定基函数和分解尺度，这样得到的结果是某一固定频带的信号，而频带的范围只与采样频率有关，与信号本身无关。EMD方法是美国学者Huang等［8］提出的一种新的时频分析方法，它将信号分解成若干个基本模式分量IMF，各IMF分量对应着不同频带的局部特征，便于更好地分析故障特征。EMD方法没有统一的基函数表达式，它依赖于信号本身，不同的信号分解后将得到不同的基函数，这样一来，EMD方法非常适用于非线性、非平稳信号的分析。

本文将EMD方法与神经网络结合起来，对轮轨噪声信号进行分析，从而实现对轮轨故障的诊断。即采用EMD对轮轨噪声信号进行处理，计算得到的各IMF分量的能量与峭度，然后以BP神经网络为分类器，把提取的各IMF分量的能量特征和各IMF分量峭度综合的多尺度峭度指标作为网络的特征参数输入，对车轮扁疤、钢轨波浪磨耗以及正常状态进行分类识别。同时，将EMD方法与小波包分析方法进行了比较分析，实验结果表明，基于EMD的神经网络方法具有更高的故障识别率。

1 EMD方法

EMD是一种能够将非平稳信号进行平稳化处理的方法，处理后的信号不同尺度的波动或趋势被逐级分解出来，形成一系列具有不同特征尺度的基本模式分量IMF。一般来说，IMF分量需要满足如下两个条件［8］：

① 整个数据序列的极值点个数与过零点个数相等或相差不超过一个；

② 在任意时间点处信号局部极大值确定的上包络线和局部极小值确定的下包络线的均值为零。

EMD方法的分解原理如下：

（1）确定待处理信号x（t）的所有局部极值点，然后用三次样条曲线将所有极大值点连接起来得到该信号的上包络线；同样，用三次样条曲线将所有极小值点连接起来得到下包络线，信号的所有数据点都处在这两条包络线之间。

（2）上、下两条包络线的均值记为 m1（t），从待处理信号 x（t）中减去 m1（t），得到 h1（t），即

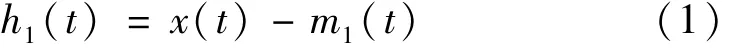
判断h1（t）是否满足IMF分量的两个条件，如果满足，就得到第一个 IMF分量，记 c1（t）＝h1（t）；如果h1（t）不满足条件，就将 h1（t）作为待处理的信号重复（1）、（2）的操作，直到 h1（t）是一个 IMF分量为止。

（3）从 x（t）中减去基本模式分量 c1（t），得到残余r1（t）：

（4）将残余 r1（t）作为待处理的信号循环（1）、（2）、（3）的操作，可以得到n个满足条件的IMF分量。

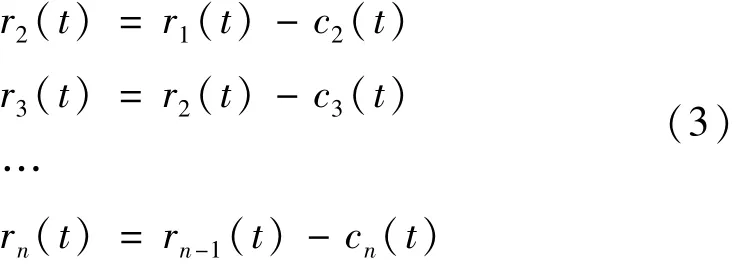
当残余rn（t）是一个单调函数，不能从中筛选出IMF分量就停止循环。这样x（t）可以表示成

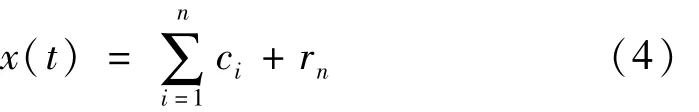
通过以上4个步骤，可以将一个信号分解成n个基本模式分量 c1（t），c2（t），…，cn（t）和残余量 rn（t）之和。残余量rn（t）反映了待处理信号的平均趋势；基本模式分量组 c1（t），c2（t），…，cn（t）表示待处理信号从高频到低频不同频段的成分，每个频段包含信号的频率成分是不同的，随着信号的变化而变化。各种故障信息就包含在这些频段中，通过分析这些频段就能够对故障进行识别，为故障检测提供方便。

图1所示为采集的车轮扁疤故障信号图。该信号进行EMD分解后得到11个IMF分量和1个残余量，如图2所示。从图中可以看出，EMD方法将车轮扁疤故障轮轨噪声信号分解成若干个IMF分量，不同的IMF包含不同的时间尺度，这样信号的特征就能够在不同的分辨率下显示出来。

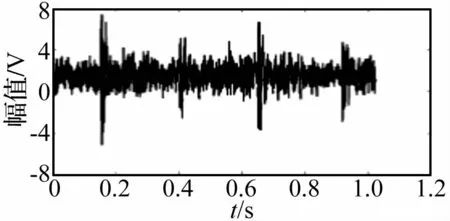
图1 所示为采集的车轮扁疤噪声信号图Fig．1 Noise signal of wheel flat

图2 车轮扁疤故障轮轨噪声信号EMD分解结果Fig．2 EMD decomposition results of wheel flat noise

2 基于EMD和神经网络的轮轨缺陷诊断

峭度系数是信号序列时域特性的数值统计量，它是一个无量纲参数指标，对信号幅值与频率的变化不敏感，只与信号概率密度函数的形状有关，表示信号概率密度函数峰顶的陡峭程度，反映的是信号中冲击成分的大小［9］。当轮轨系统存在故障，产生的轮轨噪声信号数据分布将发生变化，冲击成分的大小也将不同，其中钢轨波浪状磨耗故障和车轮扁疤故障噪声信号中都含有明显的冲击成份，因此可以选用峭度系数作为特征参数。同时，存在故障的轮轨系统与正常情况下轮轨系统产生的噪声信号相比，在相同的频带内噪声信号的能量存在较大的差异，每个频带里的能量特征变化反映了轮轨系统状态的不同，包含着相当丰富的故障信息，可以选择不同频带的能量作为特征识别不同的轮轨故障。综合以上因素，本文采用各IMF分量的能量特征与综合的多尺度峭度参数作为神经网络的特征参数输入，能够有效地对轮轨故障类型进行分类识别。

基于EMD和神经网络的轮轨故障诊断方法实现流程如图3所示。

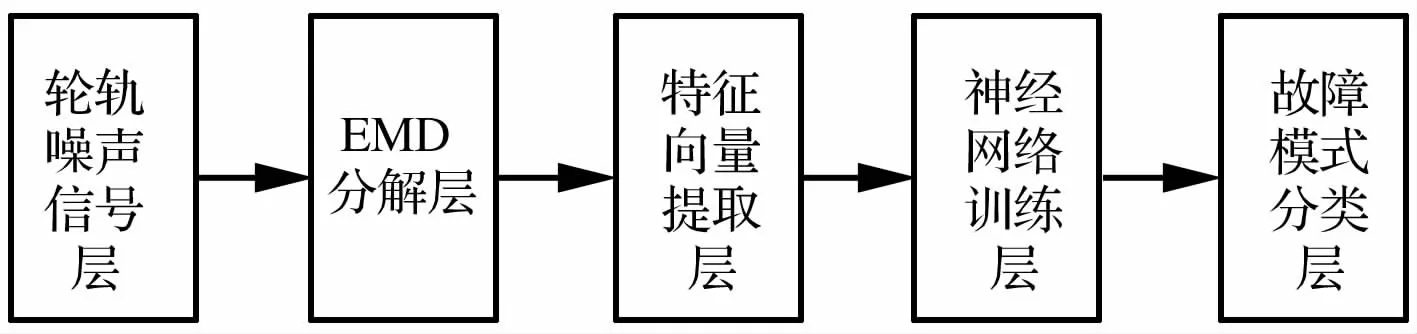
图3 基于EMD和神经网络的轮轨故障诊断实现流程Fig．3 Process of wheel／rail fault diagnosis method based on EMD and neural network

其具体步骤如下：

（1）以一定的采样频率fs对存在轮轨扁疤故障、钢轨波浪磨耗故障以及正常状态三种情况下的轮轨噪声信号分别进行N次采集，共得到3N个轮轨噪声信号样本。

（2）对每一种情况下的轮轨噪声信号进行EMD分解，得到若干个IMF分量，不同情况下轮轨噪声信号分解得到的IMF分量个数不同，考虑到轮轨故障信息大多存在于信号的高频部分，因而选择前m个含有故障信息的IMF分量作为研究对象。

（3）计算前m个IMF分量各自的能量Ei与峭度Qi，其中 i＝1，2，…，m。

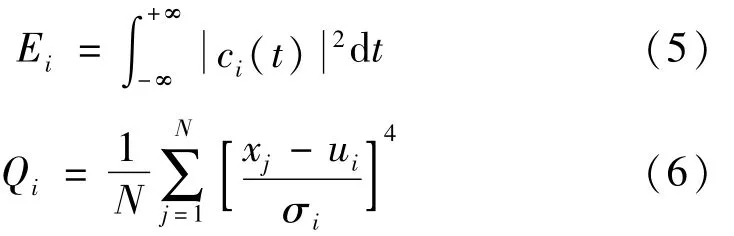
其中：ui表示第 i个IMF分量的均值，σi表示第 i个IMF分量的方差。

（4）为了实现对轮轨故障信息更好地识别，缩短训练时间，简化神经网络模型结构，将前m个IMF分量的峭度Qi进行累加，降低神经网络特征向量的维数，得到一个多尺度峭度参数dQ。

（5）构建神经网络特征向量：

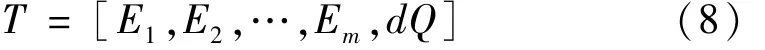
由于能量值较大，为了便于分析与处理对其进行归一化处理。

设：

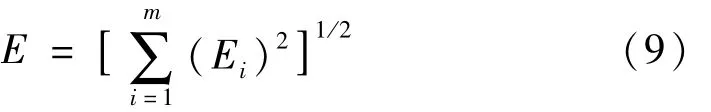
则：

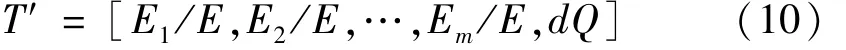
T′即为归一化后的特征向量。

（6）特征向量T′作为BP神经网络输入层参数，将本次试验的车轮扁疤故障、钢轨波浪状磨耗故障以及正常状态三种情况作为输出层参数，输出层编码为：车轮扁疤故障［1 0 0］，钢轨波浪状磨耗故障［0 1 0］，正常状态［0 0 1］。确定 BP神经网络结构，对其进行训练。

（7）将测试样本的特征参数作为网络输入，用训练好的BP神经网络进行分类识别，根据网络输出确定测试样本的状态类别。

3 实验结果

通过在实际的火车车轮或铁轨上制造缺陷的方式来获取轮轨故障噪声信号，不但影响列车的正常运行，还会造成重大的安全隐患。因而考虑模拟轮轨故障，在实验室环境下对轮轨故障噪声信号进行采集分析，该方法结合实际情况进行优化后，同样适用于对实际轮轨噪声的研究。本课题组已经完成了一套比较完备的轮轨噪声模拟采集系统［10］，本次实验就选取该设备进行轮轨噪声信号采集。轮轨噪声采集系统由传感器、数据采集卡、自制信号调理模块以及便携式计算机四部分组成。采用ISK BM－800型电容式麦克风作为噪声采集系统的传感器，通过USB－6251数据采集模块与便携式计算机中自制的labview信号调理模块连接，实现对轮轨噪声故障信号的采集。采用相似性原理，参照25G型客车按1∶15的比例搭建了实验小车及轨道系统实验平台，并设计了车轮扁疤、钢轨波浪状磨耗等缺陷，完成对轮轨故障噪声信号的采集。由于轮轨噪声频率主要分布在500 Hz至4 000 Hz的频率范围内［11］，为了避免发生混频，采样频率选为 20 000 Hz。实验小车的速度控制在0．8 m／s。本次实验模拟了车轮扁疤、钢轨波浪磨耗以及正常状态三种情况，并分别采集了三种情况下轮轨噪声信号各35组数据，每种情况各随机选取20组数据作为神经网络训练数据，其余的数据作为测试数据。

对采集到的轮轨噪声信号进行EMD分解，选取包含主要轮轨故障信息的前 8个 IMF分量 c1（t），c2（t），…，c8（t），按前述式（5）～式（9）求出特征向量 T′，由于篇幅的原因，表1只给出了每种状态1个测试样本的特征向量；采用BP网络进行分类，分别将车轮扁疤故障、钢轨波浪磨耗故障与正常状态时的特征向量T′作为神经网络的输入，因而输入层含9个单元；输出层对应着这三种不同的模式，含3个单元；经过反复实验，确定只包含一个隐层，隐层单元数根据经验公式n1＝＋a选取［12］（其中n为输入神经单元数，m为输出单元数，a为［1，10］之间的常数），最终选为12，BP神经网络结构为9×12×3。每种模式分别用20个样本进行训练，其中输入层和输出层传递函数都选为purelin，隐层传递函数选为tansig，训练方式为弹性梯度下降法，训练误差目标精度为0．000 01，算法学习速率为0．1，网络训练至收敛。用训练好的神经网络对45个测试样本进行分类识别，每种情况各15个测试样本，结果网络成功地将全部样本识别出来，表2给出了基于EMD分析方法表1对应的3个测试样本的识别结果。

对采集到的轮轨噪声信号进行小波包分析提取特征参数进行相同的神经网络训练来分类识别轮轨故障类型。由于车轮扁疤故障噪声和钢轨波浪磨耗故障噪声都存在一定的冲击成分，因此可以选择coiflet小波作为基函数。coiflet小波消失矩较大，能够适应冲击信号的突发特性及快速衰减特性，并能够突出噪声信号中冲击性信号的特征，同时避免了连续小波对信号进行时频分析时计算量过大的问题。采用coiflet小波对噪声信号进行三层小波包分解，用第三层8个频带的小波包分解系数重构出8个新的时间序列 c1（t），c2（t），…，c8（t），同样按前述式（5）～式（9）求出特征向量T′，表1给出了每种状态1个测试样本的特征向量。采用相同的神经网络对45个测试样本进行分类识别，每种情况各15个测试样本，网络识别率达到91%。表2给出了基于小波包分析方法表1对应的3个测试样本的识别结果。

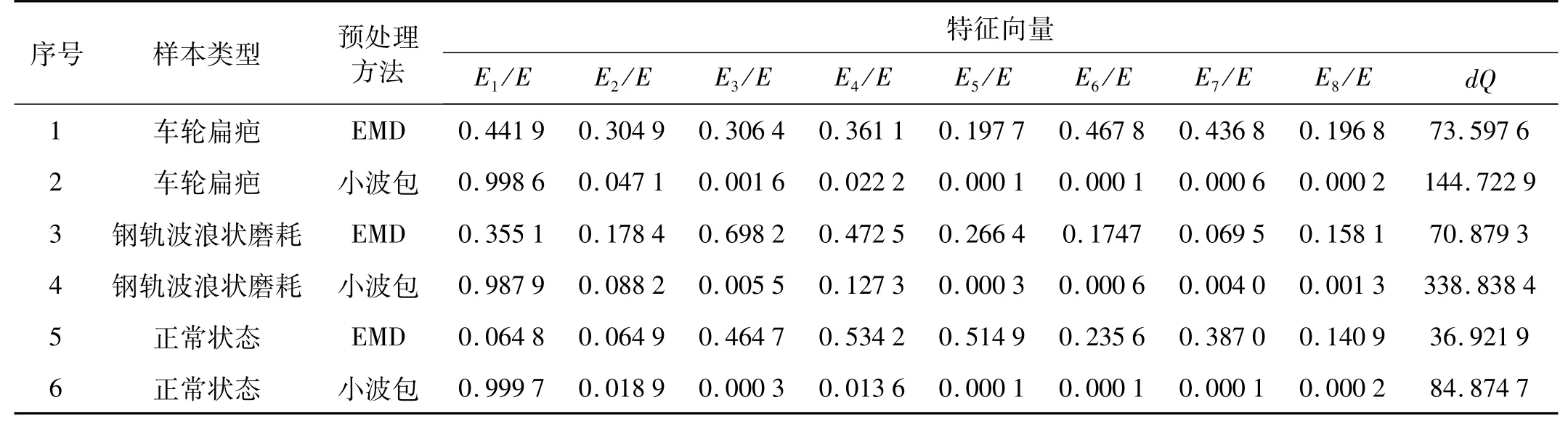
表1 各种状态下的特征向量Tab．1 Feature vectors of various states

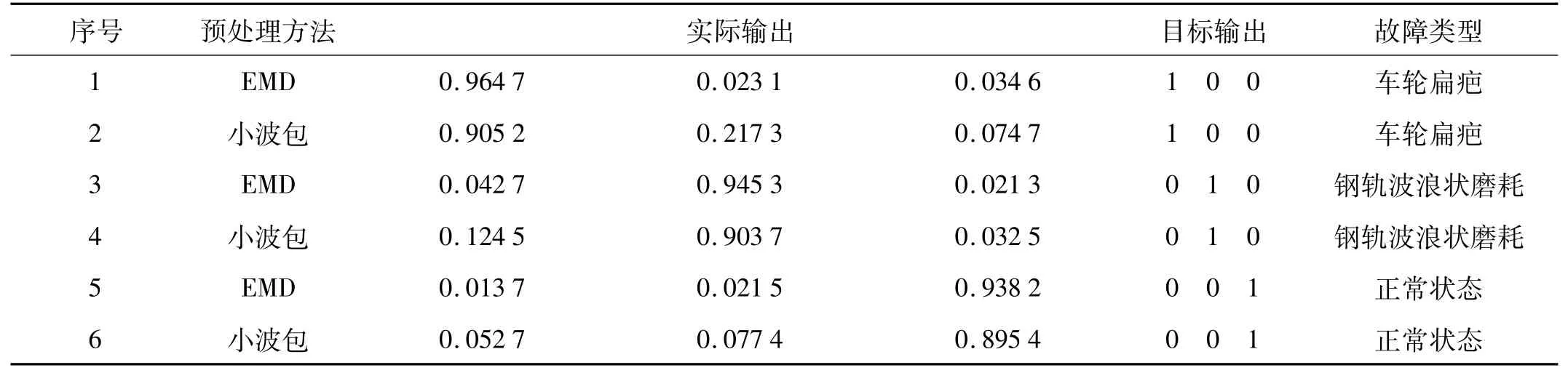
表2 神经网络诊断结果Tab．2 Diagnosis results of neural network

实验结果表明，虽然采用EMD或小波包分析方法对轮轨噪声信号进行处理，提取特征参数进行神经网络训练，都能够实现对轮轨故障的分类识别，但是基于EMD的分析方法相比于小波包分析方法具有更高的故障识别率。这是因为小波包方法不具有自适应性，分解后的各频带范围不随轮轨噪声信号的变化而变化，而EMD方法具有自适应性，依据轮轨噪声信号本身的特点进行信号分解，因而对故障信息更敏感。

4 结 论

采用轮轨噪声信号对轮轨故障进行检测是本文的创新之处。轮轨噪声信号是一种非平稳信号，当轮轨系统存在故障时，其产生的噪声信号在各频带的能量将发生变化，EMD方法能够根据信号本身的特点自适应地将信号分解到不同的频带，提取各频带的能量与峭度作为BP神经网络的特征参数输入，进而对网络进行训练，网络输出能够反映故障的本质信息。实验结果表明本文基于EMD和BP神经网络的方法能够对轮轨故障进行有效地识别，同时采用EMD方法相较于小波包方法具有更高的故障识别率。本文分析的轮轨噪声信号是在实验条件下采集的，与列车运行的实际情况存在一定的差异，然而本课题组已在进行实际列车随车噪声采集与故障识别系统的构建，基于EMD和BP神经网络的方法能够运用到随车的故障识别中。

［1］Papaellas M Ph，Robert C，Davis C L．A review on non-destructive evaluation of rails： state-of-the-art and future development［J］．Journal of Rail and Rapid Transit，2008，222：367－384．

［2］Belotti V，Crenna F，Michelini R C，et al．Wheel-flat diagnostic via wavelet transform［J］．Mechanical Systems and Signal Processing，2006，20（8）：1953－1966．

［3］Brizuela J，Fritsch C，Ibanez A．Railway wheel-flat detection and measurement by ultrasound［J］．Transportation Research Part C：Emerging Technologies，2011，19（6）：975－984．

［4］Papaelias M P，Lugg M．Detection and evaluation of rail surface defects using alternating current field measurement techniques［J］．Proceedings of the Institution of Mechanical Engineers，Part F：Journal of Rail and Rapid Transit．2012，226（5）：530－541．

［5］马旺宇，刘栋，赵文博．应用于钢轨检测的便携式涡流探伤仪的研制［J］．机械设计与制造，2010（2）：88－90．MA Wang-yu，LIU Dong，ZHAO Wen-bo．A portable eddy current flaw detector for railway testing［J］．Machinery Design＆Manufacture，2010（2）：88－90．

［6］魏祥龙，张智慧．高速铁路无砟轨道主要病害（缺陷）分析与无损检测［J］．铁道标准设计，2011，3：38－40．WEI Xiang-long，ZHANG Zhi-hui．Analysis on main defects in ballastless track on high speed railway as well as its non-damage inspection［J］．Railway Standard Design．2011，3：38－40．

［7］王鹏飞，张兴周，胡文飞．基于小波变换的火车车轮扁疤信号能量分析［J］．应用科技，2009，36（6）：25－28．WANG Peng-fei， ZHANG Xing-zhou， HU Wen-fei． The energy analysis of wheel-flat signal based on wavelet transform［J］．Applied Science and Technology，2009，36（6）：25－28．

［8］Huang N E，Shen Z，Long SR，et al．The Empirical mode of decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis［J］．Proc Royal Society，1998，454：903－995．

［9］何正嘉，訾艳阳，张西宁．现代信号处理及工程应用［M］．西安：西安交通大学出版社，2007．

［10］钟香斌．轮轨噪声模拟实验［D］．西安：西安交通大学，2010．

［11］Remington P J．Wheel／rail noise，Part I：characterization of wheel／rail dynamic system［J］． Journal of Sound and Vibration，1976，46：359－379．

［12］吕砚山，赵正琦．BP神经网络的优化及应用研究［J］．北京化工大学学报：自然科学版，2001，28（1）：67－69．L Yan-shan，ZHAO Zheng-qi．Optimization and application research of BP neural network［J］．Journal of Bejing University of Chemical Technology：Natural Science，2001，28（1）：67－69．