黏弹性阻尼夹芯板水下声辐射数值计算

胡昊灏， 商德江

（1．哈尔滨工程大学 水声技术重点实验室，哈尔滨 150001；2．哈尔滨工程大学 水声工程学院，哈尔滨 150001）

在结构表面敷设黏弹性阻尼层是船舶，飞机等航行器实现被动噪声控制的重要手段，一般有自由层阻尼和约束层阻尼（俗称夹芯板）两种敷设方式。Foin［1］比较了这两种方式在具有相同黏弹性层厚度时的降噪效果，结果表明在整个分析频带内，约束层阻尼的降噪效果都要优于自由层阻尼。

近些年来国内外关于敷设黏弹性阻尼层结构振动与声辐射的计算主要有两类方法，第一类是将阻尼层按类似流体的处理方式，白振国等［2－3］在分析敷设覆盖层的复杂圆柱壳体水下声辐射时采用了这种方法，该方法优点是计算过程较简单，但是仅限于自由层阻尼敷设方式（约束层阻尼中剪切波分量不能忽略）。第二类是采用三维弹性理论来描述覆盖层的动力学特性，陈美霞［4］在计算敷设阻尼材料的双层圆柱壳声辐射问题时，采用三维Navier方程来描述阻尼材料的运动，Berry［5］采用类似方法处理了覆盖黏弹性层的矩形板水下声辐射问题。三维弹性理论由于对应力－应变的分布没有作任何近似处理，所得结果精度高，但该方法需要给出三维弹性方程，应力和应变的边界条件，以及连续性条件，最后联合求解，这种方法计算量很大，只有在模型层数很少，加载方式，边界条件等都非常简单时才有可能求解。由于三维弹性理论计算过于繁琐，Reddy等［6－7］采用二维弹性理论（假设横向应力为零）来分析由纤维增强的复合层合板壳的动力学问题。Yin［8］和曹雄涛［9］分别采用基于 Kirchhoff假设的经典层合板理论（CLPT）和基于Mindlin假设的一阶剪切形变理论（FSDT）计算了加双周期肋骨的无限大复合层合板的声辐射问题。CLPT与FSDT待求未知数较少，计算较快，但是CLPT忽略了剪切形变的影响，仅适合薄板，而FSDT中存在剪切修正因子的确定较为繁琐的问题，且不满足板表面应力自由假设。为了避免以上问题Ghinet等［10］采用了更为精确的离散层理论来分析较厚的复合夹层结构的动力学问题，然而该方法的待求未知数随着所分析层数的增加而增加，不利于提高计算效率。

本文采用二维弹性理论中精度较高的离散层理论来分析黏弹性复合夹芯板的振动与声辐射特性，并结合传递矩阵法［11］将待求未知数的个数降到与单层板相同。需要特别指出的是上一段提到的由纤维增强复合层合板，各层均表现为各向异性，而本文要分析的黏弹性复合夹芯板则是各层均满足各向同性，因此刚度系数要作相应改变。

1 模型描述

如图1，一矩形夹芯板，其四边均简支于无限大刚性障板上，板上侧为无限大水域，下侧为真空，考虑其在谐和机械点力激励下的声辐射问题。夹芯板的底板和约束层为弹性材料，而芯层为黏弹性材料，各层材料均满足各向同性。在推导夹芯板动力学方程之前，先对模型作如下假设：

（1）对每一层材料均考虑其横向位移，膜位移以及剪切位移；

（2）认为各层的横向位移相等，也就是说沿厚度方向横向位移为常数；

（3）在各层材料的交界处满足位移以及剪切应力连续。

图1 四边简支夹芯板示意图Fig．1 Simply supported sandwich plate

1.1 位移模型

图2为夹芯板的位移场示意图，左侧为发生形变前的位移分布，右侧为底板形变后的位移分布，满足上文假设的位移场表达式为：

图2 夹芯板位移场Fig．2 Sandwich plate displacement field

式中：i分别为第i层板沿x，y方向的位移，而则分别为第i层板绕y轴和绕x轴的剪切转动位移，z（i）为第i层板中性面与底板中性面的距离。

1.2 应力应变场

为了节省篇幅，应变场按如下简化方法表示：

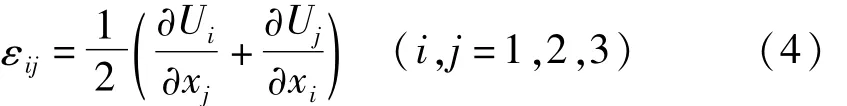
式中 U1，U2，U3分别代表 u，v，w方向的位移，而 x1，x2，x3则分别为 x，y，z方向坐标。

应力与应变关系满足胡克（Hooke）定律：

式中的Qij表示各向同性板的刚度系数。材料杨氏模量可表示为复数形式 E＝E0（1＋i*η），η为材料损耗因子。

1．3 位移传递矩阵

由假设（3）可知在各层交界处满足位移连续和剪切应力连续：

由以上连续性关系可以求出第i层与第i＋1层的位移场满足：

式中

进一步可得到第i层位移场与第1层的位移场之间的关系为：

式中［T］＝［ti－1］［ti－2］…［t1］为各层与底板位移场的传递矩阵。

2 夹芯板运动方程

2.1 系统动能

这里通过虚功原理建立系统动力学方程，首先求系统的动能

式中ec为单位面积的动能，将夹芯板各层位移表达式结合约束层及芯层与底板位移传递关系（10），可求得仅与底板位移场有关的单位面积系统动能表达式为：

其中系数m1，m2…m13为质量系数

2.2 系统的应变能

系统应变能表达式为：

式中ed为应变能密度，将应力应变关系（5）结合约束层及芯层与底板位移传递关系（10），可得到仅与底板位移场变量有关的应变能密度表达式为：

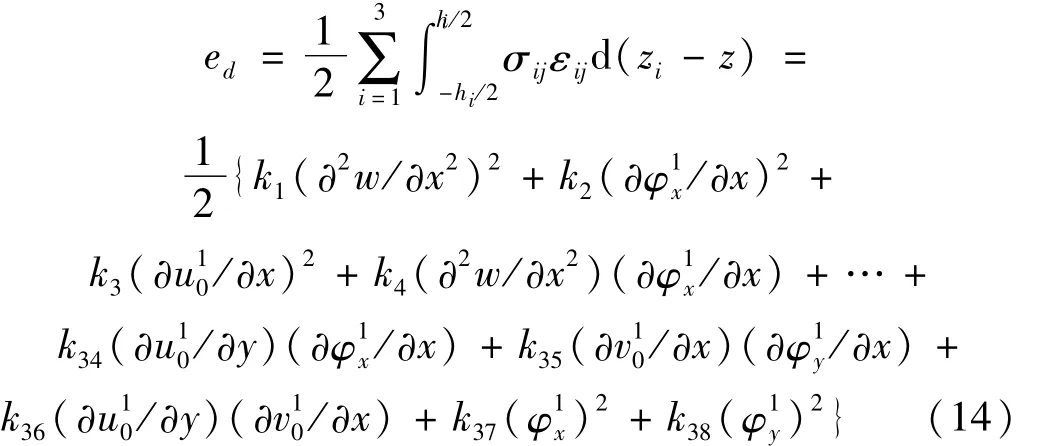
式中 k1，k2…k38为刚度系数。

2．3 外力做功：

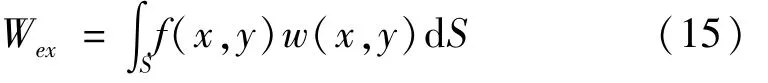
式中外力f（x，y）包括两部分：谐和机械点激励力F＝以及板表面的流体声压载荷P（x，y，t），其表达式可由 Rayleigh积分公式得到：

其中 ρ0为流体密度，k0为声场波数，w·（x′，y′）为板表面振速分布为板表面上的点与场点的距离。

由式（11），（13），（15）可得到系统的哈密顿函数（Hamiltonian）为

由上文可知，此时的哈密顿函数仅与底板的位移分量

2．4 Rayleigh-Ritz解：

因为夹芯板满足四边简支边界条件，所以可以将位移形式解设为：

为了书写简便，后文中省略了时间因子ejωt。

由虚功原理可知：

式中δ表示变分，将形式解（18）代入上式可得到仅与底板位移模态幅值有关的系统运动方程，此时方程未知数的个数由最初的15个减少到5个，因此起到提高计算效率的作用：

这里为底板的位移场向量，［M］为系统质量矩阵系统复刚度矩阵0，0，0，0｝T为外力激励。其中示板表面声压模态幅值，Zmnpq为声辐射阻抗，具体表达式可由 Rayleigh积分得到：

直接通过数值方法计算以上四重积分非常繁琐费时，通过坐标变化令 κ＝x－x′，τ＝y－y′改变积分路径，可将原来的四重积分化为二重积分［12］，以自辐射阻Rmnmn为例：

其中：

本文采用参考文献［12］中的方法将式（23）中的二重积分通过极坐标变换结合三角函数积化和差公式化为一组一重定积分，这种方法较传统的辐射阻抗计算方法［13］，计算效率有较大提高。

求解系统运动方程（20）可得到夹芯板横向位移模态幅值amn，进一步可得到系统的均方振速以及辐射声功率表达式。

3 模型验证与参数分析

3.1 算法验证

Foin等［1］给出了一四边简支的矩形夹芯板均方振速响应曲线，为了验证本文所给算法的正确性，取与Foin相同的模型进行计算，并比较两者的结果，同时也将计算结果与用有限元商业软件ANSYS所得结果对比。夹层板长为1 m，宽为0．3 m，底板和约束层均为铝板厚度分别为3 mm，0．5 mm，芯层为均匀黏弹性阻尼层，其密度为1 680 kg／m3，杨氏模量为2．6×108Pa，泊松比为0．3，损耗因子为0．6，厚度为0．5 mm，周围流体为空气，参考振速级为1，从图3可以看出本文计算结果与Foin模型的计算结果以及有限元商业软件ANSYS计算结果均有较好的一致性，从而证明了所给方法可以正确求解夹芯板的动力学问题。

图3 比较不同方法计算夹芯板均方振速Fig．3 Comparison the mean square velocity of sandwich plate with different methods

在本算例中，频率为500 Hz时，模态阶数m，n分别取15，6时计算结果收敛；1 000 Hz时 m，n分别取23，10收敛；2 000 Hz时 m，n分别取35，14收敛。很显然系统的收敛性与分析频率以及结构尺寸有关，分析频率越高所取的模态阶数越大才能满足收敛性，本算例所分析的频率范围取较低的模态阶数计算结果已经收敛。

3.2 参数分析

以下算例中所分析模型为一长1 m，宽0．5 m的夹芯板，底板与约束层均为钢板，厚度分别为0．005 m和0．002 m，芯层为黏弹性橡胶，密度为1 680 kg／m3杨氏模量为2．6×108Pa，泊松比为 0．45，损耗因子 0．6，芯层厚度为 0．01 m，激励点位置在（0．08 m，0．07 m），辐射声功率参考级为0．67×10－18W。

从图4看到，敷设约束阻尼层后，系统的辐射声功率级有明显下降趋势，尤其在中高频范围，模态峰值得到了很好的抑制。下面分析影响夹芯板声辐射的主要参数。

图4 比较夹芯板与仅有底板时辐射声功率Fig．4 Comparison sandwich plate sound radiated power with base plate alone

由图5，增加芯层厚度，在所分析的频率范围，能有效降低夹芯板的辐射声功率级，同时也能抑制大部分的高频谐振模态，因为增加芯层厚度相当于增加了系统刚度以及单位面积质量，这两方面的因素都会导致声辐射下降，且单位面积质量增加会使模态谐振峰值产生偏移。当然，并非芯层厚度越大越好，厚度太大不利于系统轻质设计要求，而且厚度过大时剪切形变对高频声辐射会有较大影响，所以合理选取芯层厚度很重要。

图6为改变芯层杨氏模量时，夹芯板辐射声功率的变化趋势，所取的杨氏模量值都是工业黏弹性材料常用到的，当杨氏模量分别取E1＝106（Pa）和E2＝107（Pa）时，两者辐射声功率变化很小，这是因为此时芯层杨氏模量与面板杨氏模量（2．6×1011（Pa））所差量级太大，改变芯层杨氏模量对整体影响不大；当杨氏模量取 E3＝2．6×108（Pa）和 E4＝7．8×108（Pa）时，后者的辐射声功率在中高频段时要低于前者，且模态峰值得到了有效抑制，这是因为增加芯层杨氏模量同样会改变系统的刚度。

图5 芯层厚度对辐射声功率的影响Fig．5 The effects of core thickness to sound radiated power

图6 芯层杨氏模量对辐射声功率的影响Fig．6 The effects of core Young’s modulus to sound radiated power

图7表明增加芯层材料的损耗因子，能有效降低谐振峰处的声辐射，但对于非谐振峰处的声辐射则没有明显的改善，且整个频带内未出现频率峰值偏移现象。

图7 芯层损耗因子对辐射声功率的影响Fig．7 The effects of core loss factor to sound radiated power

4 结 论

本文采用数值方法建立了含黏弹性材料的复合夹芯板水下振动与声辐射模型，并验证了模型的正确性，得到如下结论：

（1）将复合层合板理论中的离散层理论应用于黏弹性复合板能够正确求解复合夹芯板的动力学问题，通过传递矩阵技术结合变分法原理能够降低运动方程维数，从而提高计算效率。

（2）黏弹性材料的厚度，杨氏模量以及损耗因子是影响夹芯板声辐射的重要因素，应根据具体工况合理设置以达到噪声控制的目的。

（3）本文仅讨论了四边简支边界条件下的被动约束层夹芯板声辐射问题，为了扩充解决问题的范围，对于两对边简支，另两对边任意支承的阶梯变厚度夹芯板可沿纵向分段离散再次借用传递矩阵求解［14］。

［1］Foin O，Nicolas J，Atalla N．An efficient tool for predicting the structural acoustic and vibration response of sandwich plates in light or heavy fluid［J］．Applied Acoustics，1999，57：788－797．

［2］白振国，俞孟萨．多层声学覆盖层复合的有限长弹性圆柱壳声辐射特性研究［J］．船舶力学，2007，11（5）：107－110．BAI Zhen-guo， YU Meng-sa． Sound radiation of finite composite cylindrical shells with multi-layers acoustic coating［J］．Journal of Ship Mechanics，2007，11（5）：107－110．

［3］陶猛，范军，汤渭霖．覆盖多柔性层的有限长圆柱壳声辐射特性［J］．声学学报，2008，33（3）：220－225．TAO Meng，FAN Jun，TANG Wei-lin．The characteristics of sound radiation from a cylindrical shell coated with multiple compliant layers［J］．Acta Acustica，2008，33（3）：220－225．

［4］陈美霞，骆东平，彭旭，等．敷设阻尼材料的双层圆柱壳声辐射特性分析［J］．声学学报，2003，28（6）：486－493．CHEN Mei-xia，LUO Dong-ping，PENG Xu，et al．Analysis of characteristic of sound radiation from double cylindrical shell coated with viscoelastic layer［J］．Acta Acustica，2003，28（6）：486－493．

［5］Berry A，Foin O，Szabo J P．Three dimensional elasticity model for a decoupling coating on a rectangular plate immersed in a heavy fluid［J］Journal of the Acoustical Society of America，2001，109（6）：2704－2714．

［6］Reddy J N．Mechanics of laminated composite plates and shells：theory and analysis ［M］． CRC press，Boca Raton，2004．

［7］杨坤，梅志远，李华东．黏弹性复合材料夹芯板稳态响应分析［J］．振动与冲击，2013，32（7）：88－92．YANG Kun，MEI Zhi-yuan，LI Hua-dong．Steady response analysis for a composite sandwich plate with viscoelastic core layer based onKelvin model［J］．Journal of Vibration and Shock，2013，32（7）：88－92．

［8］Yin X W，Gu X J，Cui H F．Acoustic radiation from a laminated composite plate reinforced by doubly periodic parallel stiffeners［J］Journal of Sound and Vibration，2007，306（3－5）：877－889．

［9］Cao X，Hua H，Zhang Z．Sound radiation from shear deformable stiffened laminated plates［J］Journal of Sound and Vibration，2011，330（16），4047－4063．

［10］ Ghinet S，Atalla N．Diffuse field transmission into infinite sandwich composite and laminate composite cylinders［J］．Journal of sound and vibration，2006，289（4－5）：745－778．

［11］Loredo A，Plessy A，Hafidi A E．Numerical vibroacoustic analysis of plates with constrained-layer damping patches［J］．Journal of the Acoustical Society of America，2011，129（4）：1905－1918．

［12］Li W L，Gibeling H J．Determination of the mutual radiation resistances of a rectangular plate and their impact on the radiated sound［J］．Journal of Sound and Vibration，2000，229（5）：1213－1233．

［13］沈苏，刘碧龙，李晓东．两种简支矩形板辐射阻抗计算方法的对比研究［J］．声学技术，2007，26（5）：15－16．SHEN Su，LIU Bi-long，LI Xiao-dong．Comparison of two calculation methods of radiation impedance of a simplysupported rectangular panel［J］．Technical Acoustics，2007，26（5）：15－16．

［14］向宇，袁丽芸，陆静，等．环状分块覆盖ACLD圆柱壳振动分析的新矩阵法［J］．振动工程学报，2010，23（3）：275－282．XIANG Yu，YUAN Li-yun，LU Jing，et al．A matrix method for analyzing vibration of a circular cylindrical shell with ring blocking active damping layer［J］．Journal of Vibration Engineering，2010，23（3）：275－282．