大跨屋盖结构风致背景响应和共振响应实用组合方法

李玉学，杨庆山，田玉基，向 敏

（1．石家庄铁道大学 土木工程学院，石家庄 050043；

2．石家庄铁道大学 道路与铁道工程安全保障省部 共建教育部重点实验室，石家庄 050043；3．北京交通大学 土木建筑工程学院 结构风工程与城市风环境北京市重点实验室，北京 100044）

Davenport［1］将背景响应和共振响应的概念引入结构风工程计算，由于该求解思路能够较好地反映风荷载对结构的作用机理，因而得到了广泛应用并不断发展［2－6］。已有研究表明，基于该思路求解大跨屋盖结构的风振响应常常需要涉及各参振模态内和模态间背景响应、共振响应的耦合效应，即结构响应的合理组合问题［7－10］。

围绕上述问题，国内外很多学者提出了多种处理方法。Gu等［8］为了得到考虑模态间耦合效应的共振响应合理组合，提出将参振模态共振响应的SRSS（平方和开方）组合结果乘以一个修正系数来考虑模态间耦合项的贡献；罗楠等［9］通过对频响传递函数的分析，给出了参振模态共振响应的简化CQC（完全二次型）组合方法，以实现模态共振响应的高效组合。Ke等［10］研究背景响应和共振响应间耦合项发现，其所占脉动风总响应的比例甚至达到20%，并提出了补偿该耦合项贡献的一致耦合法。Holmes［11－12］采用静力方法计算总背景响应，并采用SRSS法组合多阶模态共振响应得到总响应，该方法有效考虑了背景响应的模态耦合效应，但忽略了共振响应模态耦合效应的影响，且背景响应和共振响应能否采用SRSS组合也值得商榷。李玉学等［13］通过构造模态耦合系数选取耦合主导模态，在此基础上，考虑模态耦合的总背景响应和共振响应可以由各参振模态响应的SRSS组合结果叠加耦合主导模态的贡献得到，该方法的缺陷在于背景响应的计算也需要在各参振模态上分解，且省略了高阶模态的贡献，计算效率和精度受到影响。田玉基等［14］通过求解背景响应和共振响应相关系数，并采用CQC法组合了北京奥林匹克公园网球中心赛场屋盖的竖向位移响应，达到了较高的计算精度，但计算过程比较复杂。

本文将基于随机振动理论，分析推导背景响应及其模态耦合项、共振响应及其模态耦合项、背景响应与共振响应耦合项的表达式，并给出考虑耦合效应的脉动风总响应组合公式。在此基础上，引入耦合效应修正系数，根据结构动力特性和风荷载特性对该组合公式简化分析，据此实现考虑耦合效应的大跨屋盖结构风致背景响应和共振响应实用高效组合。

1 背景、共振分量定义及其传统组合方法

大跨屋盖结构在脉动风荷载作用下的运动方程为：

式中：M、C和K分别为结构的质量、阻尼和刚度矩阵；分别为加速度、速度和位移向量；P（t）为测压点处的脉动风荷载，L表示测压点与节点间等效力转换矩阵。

按照背景响应的概念，将脉动风荷载作用下的结构振动看作拟静力过程，即忽略式（1）中的动力项，可以得到结构背景响应的控制方程：

求解方程（2）得背景响应：

按照模态叠加法，选取一定数量的主导模态（对结构响应贡献较大的模态，记为m阶）参与计算，主导模态的选取参见文献［15］，则式（1）中的结构位移响应可以表示为：

式中为m阶主导模态组成的模态矩阵，j为第 j阶参振模态的模态向量；为 m阶主导模态广义模态坐标组成的列向量，qj（t）为第j阶参振模态的广义模态坐标；“T”表示矩阵转置；Qb（t）和Qr（t）分别为 Q（t）相应地背景分量和共振分量。

同理，由模态背景响应的概念，Qb（t）可以通过静力分析得到，即：

式中阶主导模态广义柔度矩阵，diag［·］表示取对角线元素组成的对角矩阵为第j阶参振模态的圆频率；F（t）为广义模态力列向量。

将式（5）代入式（4）可以得到共振响应：

至此，按照随机振动理论，结构某一自由度i上总响应方差可以由式（3）表示的背景响应 Xd，b（t）和式（6）表示的共振响应 Xd，r（t）组合得到：

式中得到的结构第 i自由度上背景响应方差和共振响应方差；ρx，b，r，i为由 Xd，b（t）和 Xd，r（t）得到的结构第 i自由度上背景响应和共振响应的相关系数，计算公式为：

式中 Sx，b（ω）、Sx，r（ω）、Sx，b，r（ω）分别为背景响应谱矩阵、共振响应谱矩阵及二者耦合项响应谱（响应互谱）矩阵；diag［·］i表示对角矩阵diag［·］中与结构第 i个自由度对应的元素。

式（7）中最后一项即为背景响应和共振响应的耦合项，需要通过式（8）计算相关系数 ρx，b，r，i求得，而ρx，b，r，i的计算需要涉及繁琐的双重求和与积分运算，因此在工程实践中常常将其省略，采用不考虑背景、共振耦合项的SRSS组合，即：

研究表明，对于大跨屋盖结构风振响应计算，SRSS组合常常不能得到理想的结果［10，14］。本文将基于背景响应、共振响应及二者耦合项的分析推导，给出其考虑耦合效应的实用组合方法。

2 考虑耦合效应的背景、共振响应实用组合

2.1 背景响应及其耦合项

由公式（3）得背景响应的相关函数：

式中E［·］表示数学期望；Rpp（τ）表示脉动风荷载的互相关矩阵，τ为虚时间变量。

对式（10）作傅里叶变换，得背景响应功率谱：

式中SPP（ω）为脉动风荷载互谱矩阵。

由式（11）得背景响应方差：

式（12）包含了所有模态及其耦合项对背景响应的贡献，取其对角线元素可以得到结构某一自由度i上的背景响应方差：

式中 Sbibi（ω）为 K－1LSPP（ω）LTK－1T第 i个对角线元素为荷载方差矩阵。

2.2 共振响应及其耦合项

同理，由式（6）可以得到共振响应的相关函数：

对式（14）作傅里叶变换，得共振响应功率谱：

式中为第j阶模态的频响函数，i为虚数单位；Hr（ω）为共振响应的频响函数矩阵。

由式（15）可以得到共振响应方差：

式（16）为共振响应的CQC组合表达式，包含了各阶主导模态及其模态耦合项对共振响应的贡献，由此可得结构某一自由度i上的共振响应方差：

式中：j，i、k，i分别表示第 j阶和第 k阶模态在结构第 i自由度上的值Lk为第 j阶和第 k阶模态力谱为第 j阶模态共振响应频响函数为结构第 i自由度上第 j阶模态共振响应方差i为结构第 i自由度上第 j阶和第k阶模态耦合项共振响应方差。

式（17）右边第一项为m阶主导模态对共振响应的贡献（SRSS组合）；第二项为模态耦合项对共振响应的贡献。

2．3 背景响应与共振响应耦合项

由式（3）和式（6）可以得到背景响应和共振响应耦合项的相关函数：

对式（18）作傅里叶变换，得背景响应和共振响应耦合项功率谱：

由式（19）得背景响应和共振响应耦合项的方差：由式（20）可以得结构某一自由度i上的背景与共振耦合项位移响应方差：

式中 SBiBi（ω）为矩阵 K－1LSPP（ω）LT第 i个对角线元素；σ2x，b，r，j，i为结构第 i自由度上第 j阶模态共振响应与背景响应耦合项位移响应方差。

2．4 总响应实用组合

由式（13）、（17）、（21）可以得到结构某一自由度 i上总响应方差：

式（22）包含了背景响应及其模态耦合项、共振响应及其模态耦合项、背景响应与共振响应耦合项三部分。与式（7）传统组合方式不同的是，背景响应与共振响应耦合项不再通过求解相关系数 ρx，b，r，i得到。

为简化计算，将式（22）进一步表示为：

cji定义为耦合效应修正系数，其大小反映了结构第i自由度上计入第j阶模态共振响应与背景响应的耦合项后对第j阶模态共振响应的影响，因此可以通过该系数来考虑背景响应与共振响应的耦合效应。

为简化计算，需要根据结构动力特性和风荷载特性对cji进行简化处理。

式中H第 j阶模态共振响应频响函数的实部，由于）虚部对结构响应影响不大，为简化分析，只取其实部［16］。H*j，r在频域内的分布如图 1所示，表达式为：

式中

图1 频域分布示意图Fig．1 Schematic diagram of

由图1可见，在低频段其值几乎为零，在结构自振频率ωj附近发生符号变换，且在ωj附近有一个窄带峰值区，在其他频域段其值相对较小，据此可将其在频域内离散处理：

式中 Δj为第 j阶模态的共振区间宽度；Hj，rmax，Δj、Hj，rmin，Δj分别表示在共振区间 Δj内的最大值和最小值；

结合式（27），可将式（25）离散表示为：

其中：

由图1可见，在共振区间 Δj内，由极大值到极小值发生突变，故在 Δj内可将其近似看作线性变化，即：

式中处的值。

对于大跨屋盖结构，风荷载谱SPP（ω）在风荷载卓越频率ω0处有一峰值，其后在高频段迅速衰减，如图2所示。风荷载属于低频荷载，通常风荷载的卓越频率ω0远小于结构自振频率忽略，由此可得：

图2 SPP（ω）频域分布示意图Fig．2 Schematic diagram of SPP（ω）

式（24）中 σ2x，j，r，i，可以进一步表示为：

图 3 ｜Hj，r（ω）｜2频域分布示意图Fig．3 Schematic diagram of｜Hj，r（ω）｜2

由图 3可见在低频段其值几乎为零，在结构自振频率ωj附近的窄带峰值区内有一峰值，在高频段其值相对较小，据此可将式（36）在频域内离散处理：

式（44）右边第一项为背景响应，考虑了所有模态及其耦合项的贡献；右边第二项为m阶主导模态共振响应及其与背景响应耦合项的贡献，该耦合项通过耦合效应修正系数cji计及，而cji的计算不再涉及复杂的求和与积分运算，由结构动力特性参数和风荷载参数即可方便求得；右边第三项为m阶主导模态共振响应模态耦合项的贡献。可见，该组合公式有效考虑了参振模态间和模态内背景响应和共振响应的耦合效应，且方便组合。

3 算例分析

根据本文给出的实用组合公式，采用FORTRAN语言编制了计算程序，以国家体育场屋盖主结构为例，对其风致背景响应、共振响应进行了组合计算。为了比较，还分别采用传统方法（CQC法和SRSS法）对结构风振响应进行了组合计算。

3.1 国家体育场结构形式及风洞试验简介

国家体育场屋盖主结构由围绕中间环梁呈放射状布置的48榀格构式刚架组成，刚架由周边24根组合柱支撑。主体建筑为椭圆型，长轴和短轴方向最大尺寸分别为332．3 m和296．4 m，屋盖顶面呈鞍型，中间开洞长、宽尺寸分别为185．3 m和127．5 m，屋盖主结构及次结构形成了“鸟巢”的特殊建筑造型，如图4所示。该结构建筑体型复杂，属于风敏感结构，无法从现行荷载规范中获得相应的风荷载数据，需要通过风洞试验确定结构表面的实际风荷载，为结构抗风设计提供依据。

图4 国家体育场屋盖结构计算模型Fig．4 Calculation model of National Stadium roof structure

国家体育场屋盖结构风洞试验在BMT流体力学有限公司完成，风洞测试区宽4．8 m、高2．4 m、长15 m，风洞试验中模型的几何缩尺比为1∶300，并被安装在一个直径4．4 m的多板转台上，同时模拟距离场地中心450 m半径范围内周边建筑的影响，地面粗糙度类别取B类，基本风压取0．5 kN／m2，换算到体育场檐口高度（作为基准高度）处的设计风速为32 m／s，基准高度处湍流强度约为17%，在内外屋盖的上下表面以及中间环梁屋面的两个侧面共布置了509个测压点，试验模型采样频率为500Hz，每个测点采集98 000个数据，以10°为间隔，共采集了36个不同风向角下的风荷载数据，其中340°风向角为盛行风向，本文算例分析采用的风荷载为340°风向角时的测压数据，风向角的定义如图5所示。

图5 典型控制节点位置编号及风洞试验中风向角定义Fig．5 Position and number of key nodes and wind position of wind tunnel test

3.2 风洞试验数据处理及结构自振特性分析

在风振响应计算时，为方便风荷载的施加，将整个屋盖划分为74个板块，如图6所示。分别将内外屋盖上下表面测得的风荷载合并在一起，并认为每个板块内部的风压相同，其值由板块内部所有测压点风荷载数据取平均得到。

图6 风荷载加载板块示意图Fig．6 Load panel of wind load

为了计算结构在已测风荷载作用下的风致响应，还需要结构的自振频率、振型等模态信息，为此本文在ANSYS中建立了结构有限元计算模型（图4），并进行自振特性分析，提取了结构前500阶模态的自振频率和振型，图7给出了前500阶模态自振频率分布。

图7 国家体育场前500阶自振频率分布Fig．7 Ahead 500 mode natural frequency distribution of National Stadium roof structure

由图7可以看出，结构自振频率较低，且分布密集，在0．9Hz到8．1Hz之间分布了500阶模态，模态响应间的耦合效应会比较显著，因此结构风致响应组合计算需要考虑模态间耦合项的贡献。

3．3 典型节点风致响应组合计算结果

根据文献［15］所提选取主导模态的方法，从该结构自振特性分析提取的前500阶模态中选取第1阶、第2阶、第4阶、第3阶、第7阶、……共33阶作为主导模态参与结构风振响应计算。

利用风荷载测压试验得到的结构表面风荷载数据以及自振特性分析得到的结构自振频率、振型等模态信息，分别按照式（44）本文所提组合方法、式（7）传统组合方法（CQC法，作为精确值）以及式（9）不考虑耦合效应的SRSS组合方法计算了结构的竖向位移极值响应。

取响应数值较大的屋盖内环上28个节点为典型控制节点，典型控制节点位置及编号如图5所示，篇幅限制，只选取其中6个典型控制节点的计算对比结果列于表1。

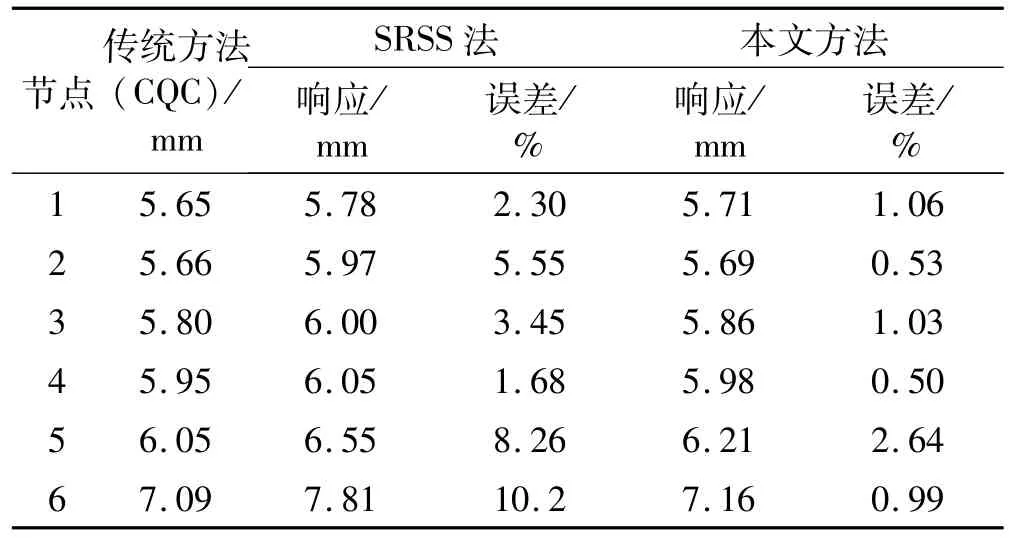
表1 典型控制节点竖向位移极值响应组合计算结果对比Tab．1 Comparison of extreme vertical displacement response of dominate nodes

从表1中可见，不考虑耦合效应的SRSS组合计算结果与传统组合方法（CQC法，精确值）的计算结果差别较大，其中位移响应较大的6号节点误差达到了10．2%，说明该节点模态耦合效应显著，若省略耦合项的贡献，这一误差在工程中是不允许的，可见对于大跨屋盖结构风振响应计算需要考虑模态耦合效应。采用本文提出的实用组合方法，其计算结果与传统组合方法（CQC法，精确值）的计算结果比较接近，误差基本控制在3%以内，说明本文提出的实用组合方法有效考虑了耦合效应，对于工程应用具有较高的精度。

为了进一步分析该屋盖结构背景响应和共振响应耦合效应特性，根据本文对耦合效应修正系数的定义，还专门提取了28个节点典型控制节点的耦合效应修正系数值，篇幅限制，表2只列出了其中12个典型控制节点的计算结果。

表2 典型控制节点耦合效应修正系数计算结果Tab．2 Calculation results of the coupling effect modification coefficient

从表2中可见，所列12个典型控制节点的耦合效应修正系数值都超过了5%，其中最大的7号节点达到了28．89%，且基本均为负值，再次表明大跨屋盖结构风致背景、共振响应组合计算考虑耦合效应的必要性，否则可能会高估结构的实际响应。

4 结 论

本文主要对大跨屋盖结构风振响应计算中考虑耦合效应的背景响应和共振响应合理组合方法进行了研究，主要结论有：

（1）以随机振动理论为基础，推导了大跨屋盖结构风致背景响应及其模态耦合项、共振响应及其模态耦合项以及背景响应和共振响应耦合项的表达公式，同时给出了考虑模态耦合效应的脉动风总响应组合公式。

（2）引入了耦合效应修正系数，通过该系数对背景响应和共振响应的耦合项进行补偿，并根据结构动力特性与风荷载特性对脉动风总响应组合公式进行了简化分析，得到了相应的实用组合公式，实现了大跨屋盖结构考虑耦合效应的风致背景响应和共振响应高效组合，避免了繁琐复杂的传统CQC组合计算。

（3）根据本文所提背景响应和共振响应实用组合方法，对国家体育场屋盖主结构风振响应进行了组合计算，并与传统统组合方法（CQC法和SRSS法）计算结果进行对比。结果表明，大跨屋盖结构风致背景响应和共振响应组合计算需要考虑耦合效应，否则可能会高估结构的实际响应。同时，也验证了本文所提方法计算精度接近CQC法的计算精度，能够满足工程需要。

［1］Davenport A G．Gust loading factors［J］．Journal of the Structural Division，1967，93（3）：11－34．

［2］Ashraf A M，Gould P L．On the resonant component of the response of single degree of freedom system under wind loading［J］．Engineering Structures，1985，7（4）：280－292．

［3］Davenport A G．How can we simplify and generalize wind loads［J］．Journal of Wind Engineering and Industrial Aerodynamics，1995，54：657－669．

［4］Zhou Y，Kareem A，Gu M．Equivalent static buffeting wind loads on structure［J］．Journal of Structural Engineering，2000，126（8）：989－992．

［5］Chen X Z，Kareem A．Equivalent static wind loads on buildings：new model［J］．Journal of Structural Engineering，2004，130（10）：1425－1435．

［6］李瞡，韩大建．屋盖风振响应功率谱及背景与共振响应的分离［J］．工程力学，2010，27（6）：65－71．LI Jing， HAN Da-jian． Power spectra of wind-induced response and separation of background response from resonant response for roof structures［J］．Engineering Mechanics，2010，27（6）：65－71．

［7］Chen X Z，Kareem A．Coupled dynamic analysis and equivalent static wind loads on buildings with three-dimension modes［J］．Journal of Structural Engineering，2005，131（7）：1071－1082．

［8］Gu Ming， Zhou Xuan-yi． An approximation method for resonant response with coupling modes of structures under wind action［J］．Journal of Wind Engineering and Industrial Aerodynamics，2009，97（11）：573－580．

［9］罗楠，廖海黎，李明水．大跨屋盖结构共振响应的简化CQC法［J］．西南交通大学学报，2012．47（6）：916－920．LUO Nan， LIAO Hai-li， LI Ming-shui． Simplified CQC method for resonant response of long-span roof structure［J］．Journal of Southwest Jiaotong University，2012．47（6）：916－920．

［10］Ke S T，Ge Y J，Zhao L，et al．A new methodology for analysis of equivalent static wind loads on super-large cooling towers［J］．Journal of Wind Engineering and Industrial Aerodynamics，2012，111（3）：30－39．

［11］Holmes J D．Along-wind response of lattice towers［J］．Engineering Structures，1996（7）：483－496．

［12］Holmes J D．Effective static load distributions in wind engineering［J］．Journal of Wind Engineering and Industrial Aerodynamics，2002，90（2）：91－109．

［13］李玉学，杨庆山，田玉基．大跨屋盖风致背景响应和共振响应的模态耦合［J］．振动工程学报，2009，22（6）：614－619．LI Yu-xue，YANG Qing-shan，TIAN Yu-ji．Modal coupling effects for wind-induced background response and resonant response of large-span roof［J］． Journal of Vibration Engineering，2009，22（6）：614－619．

［14］田玉基，杨庆山．北京奥林匹克公园网球中心赛场悬挑钢屋盖结构风振响应分析［J］．建筑结构学报，2009，30（3）：126－132．TIAN Yu-ji，YANG Qing-shan．Wind-induced response of cantilevered steel roof of olympic park tennis center stadium［J］． Journal of Building Structures，2009，30（3）：126－132．

［15］李玉学，杨庆山，田玉基．大跨屋盖结构风振响应主要参振模态确定方法研究［J］．计算力学学报，2010，27（6）：1049－1054．LI Yu-xue，YANG Qing-shan，TIAN Yu-ji．Research on the method for selecting dominant modes of wind-induced response for large-span roofs［J］． Chinese Journal of Computational Mechanics，2010，27（6）：1049－1054．

［16］Simiu E，Scanlan R H．Wind effects on structures［M］．New York，John Wiley＆Sons，Inc．，1996．

［17］沈国辉．大跨度屋盖结构的抗风研究［D］．杭州：浙江大学，2004．

［18］武岳，吴迪，孙瑛．结构风振分析中的脉动风荷载频率补偿方法［J］．振动工程学报，2010，23（5）：480－486．WU Yue，WU Di，SUN Ying．The frequency compensation of fluctuating wind loads in wind-induced response analysis［J］．Journal of Vibration Engineering，2010，23（5）：480－486．

［19］王国砚．基于高精度数值积分的结构顺风向风振计算［J］．力学季刊，2006，27（1）：162－167．WANG Guo-yan．On computation of along wind structural vibration based on numerical integration with high resolution［J］．Chinese Quarterly of Mechanics，2006，27（1）：162－167．