基于橡胶垫－质量块系统放大效应的子结构振动台试验方法

蔡新江，田石柱，3，王 彬

（1．苏州科技学院 土木工程学院，苏州 215011；2．江苏省结构工程重点实验室，苏州 215011；3．哈尔滨工业大学 土木工程学院，哈尔滨 150090）

随着高性能材料的出现、计算分析的精细化和施工技术水平的改善，尤其是结构控制和结构健康监测等高新技术的应用，使得高层建筑的抗震性能得到了极大的提高，目前的技术水平已经能够实现主体结构在设防地震作用下基本保持完好，在大震作用下主体结构也能维持在可接受的损伤范围内并能在震后及时进行修复。然而，高层建筑的顶部可能产生过大的位移反应和加速度反应，使得非结构构件和室内设备的损坏可能非常严重，一方面，可能对人造成伤害，并且过大的地震反应也会影响居住者的舒适度；另一方面，影响使用功能可能造成较大的经济损失，例如，股票交易所无法进行交易导致的经济损伤可能比修复结构的费用大很多，最近几年发生的几次地震证实了上述情况。地震作用下高层建筑的反应随着高度的增加而逐步加大，因此，高层建筑尤其是顶层的反应再现模拟是一个非常值得深入研究的问题。

从计算角度来说，利用有限元分析可以较为精确地得到高层建筑的顶部反应，但对非结构构件和室内设备的反应再现模拟则必须要借助于试验的手段。抗震试验方法主要有三种：拟静力试验、振动台试验和拟动力试验，其中，振动台试验能较好地实现地震反应模拟，但相似比为1／10～1／50的高层建筑整体结构缩尺模型试验显然无法进行非结构构件和室内设备的模拟，替代的方法是使用子结构试验方法，即在满足振动台承载能力的基础上，将结构顶部几层制作大比例模型放置于振动台上进行试验，但问题在于需要在台面上实现子结构模型底部所处楼层位置的反应，即意味着满足较大的加速度、速度、位移和油源流量需求，对于目前的振动台试验依然是不可实现的。

1 子结构振动台试验方法

1.1 研究现状

为解决振动台承载能力和台面尺寸对大型结构试验的限制，国内外学者对子结构振动台试验方面进行了积极的探索。

Igarashi等［1］对一个 65 m高的桥墩 TMD减振结构进行了试验研究，桥墩按第一振型简化为单自由度结构，试验子结构为 TMD。Lee等［2］通过对单自由度结构TLD控制作用下传统振动台试验与子结构振动台试验的结果进行对比，认为两者结果能够精确的吻合。Kausel等［3－4］阐述了单自由度和多自由度的振动台－拟动力混合试验，该方法将外部激励分为两部分，一部分由振动台施加，另一部分由作动器施加。不同的激励划分方法明显降低了试验能耗、降低对作动器行程与推力的要求、并可由单向振动台实现双向振动试验功能以及提高试验精度等。美国纽约州立大学布法罗分校Reinhorn等［5－6］利用振动台和振动台－反力墙对两层钢框架结构进行了振动台试验，其底层作为试验子结构，顶层作为数值子结构。他们着重研究了试验子结构与振动台的相互作用，提出在振动台与试件之间加设弹簧以补偿自然速度反馈的影响。

程绍革等［7－8］基于子结构模态综合法对大型复杂结构的振动台混合试验技术进行了研究，采用对接加载主模态修正方法对试验子结构进行质量矩阵和刚度矩阵局部修正，并给出了连接边界的加载模式，该方法把振动台试验与拟动力试验结合起来，算例分析表明利用子结构模态综合技术是解决混合试验技术的一条途径。田石柱等［9］提出了位移控制加载的振动台混合试验方法，建立了基于MTS电液伺服加载装置的混合试验系统，完成了以底层框架为试验子结构的三层钢框架的振动台混合试验，验证了振动台混合试验方法的可行性。李振宝等［10］对四种界面反力的获取方法进行了理论推导和对比分析，并通过钢框架结构模型振动台试验进行分析验证，最后给出了4种方法的适用条件及使用建议。

Nakashima等［11－12］利用 E-defense进行了两个典型试验：30层钢框架结构的振动台试验，以上部5层钢框架作为试验子结构模型，底部放置两层橡胶－质量放大系统来模拟下部结构对上部子结构的相互作用；21层钢框架结构的振动台试验，以底部4层钢框架作为试验子结构模型，利用橡胶－混凝土板－阻尼器系统模拟上部结构对下部试验子结构的相互作用。

1.2 橡胶垫－质量块系统放大原理

橡胶垫－质量块系统放置在试验子结构模型底部，与振动台刚接，橡胶垫具有稳定的弹性变形，可以模拟下部结构的水平刚度和大变形情况，质量块可以模拟下部结构的质量，原理如图1所示。

图1 橡胶－质量系统子结构振动台试验示意图Fig．1 Schematic of substructure shaking table test with rubber and mass system

地震作用下结构的运动方程为：

由动力放大系数随阻尼比和频率的变换关系可知：，结构加速度反应减小，即为隔震体系；当结构加速度反应加大。质量垫－质量块系统通过合理调节橡胶垫的刚度和集中质量块的质量，并通过传递函数修改输入地震动，使放大结构的加速度响应，克服了传统振动台试验在位移、加速度等方面的限制，可使子结构的顶层加速度反应与原结构的顶层加速度反应相似。

2 新输入地震动

2.1 传递函数

为了使子结构能够准确地再现原结构顶层加速度响应，不能直接采用原地震动输入，而需要产生一条新的地震动输入。已知结构特性和地震响应，求结构的输入属于输入反演问题，其关键为求解系统的传递函数。

振动台输入和模型响应分别设定为系统的输入和输出，则系统的状态空间表达式和观测方程可表述为：

式中状态向量由相对位移向量

d（t）和相对速度向量d·（t）组成，y（t）表示结构加速度响应，u（t）表示地震输入，A、B、C分别为：

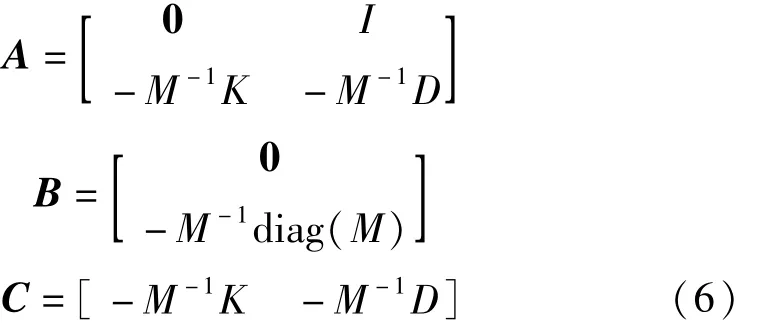
式中M、K、D分别为结构的质量矩阵、刚度矩阵和阻尼矩阵，I为单位矩阵，0为零向量。

对（5）式进行拉普拉斯变换，则可得

初始位移d（t）＝0和初始速度d·（t）＝0，则初始条件x0＝0，则传递函数为：

2.2 数值算例

选择一个3自由度体系验证传递函数的有效性，假定集中质量 m1、m2、m3分别为 2 762 kg、2 760 kg和2 300 kg，刚度 k1、k2、k3分别为 24．85 N／m、19．21 kN／m和 15．22 kN／m，此时 ω1＝1．29 rad／s，ω2＝3．32 rad／s，ω3＝4．73 rad／s，假设结构 1阶和 2阶振型阻尼比ξ1＝0．05、ξ2＝0．07，阻尼矩阵采用瑞利阻尼，C＝α1M＋α2K。

采用峰值加速度为1 m／s2的EI Centro地震动，采样周期0．02 s，时间取前10 s，基于matlab采用时程分析法求解结构地震反应，结构顶层加速度反应如图2所示。

图2 结构顶层加速度反应Fig．2 Acceleration response of structure top floors

已知结构特性M、K、D分别为：

将传递函数和结构顶层加速度反应进行卷积即可求得新输入地震动曲线。图3为两者对比曲线。由图可见：求得的新地震动输入曲线和原地震动输入曲线几乎相同，在最大加速度处吻合的很好，只在部分加速度值处略有偏差。从傅里叶谱对比可以看出两条曲线的吻合度很高，经传递函数求得的加速度曲线的频率、相位都未发生偏移，具备较高的计算精度，能够满足试验和数值仿真时的精度要求。

图3 新输入地震动与原输入地震动对比曲线Fig．3 Compared curve between new and old earthquake input

3 验证试验

3.1 振动台设备及系统

试验设备为北京波谱世纪科技发展有限公司生产的WS－Z30－40小型电磁式振动台，由振动台面、电磁式激振器、功率放大器、控制传感器、控制和采集仪、计算机以及系统软件等组成，其技术指标如表1所示，所使用的控制软件为Vib’SQK（V2．1），在振动台台面上安装加速度传感器来测量地震动输入。

表1 WS－Z30－40技术指标Tab．1 Technical index of WS－Z30－40

本文进行的是结构动力试验，需要考虑动力相似问题，基于几何特性、材料特性和动力性能的相似，采用弹塑性模型，主要物理量的动力相似关系如表2所示。

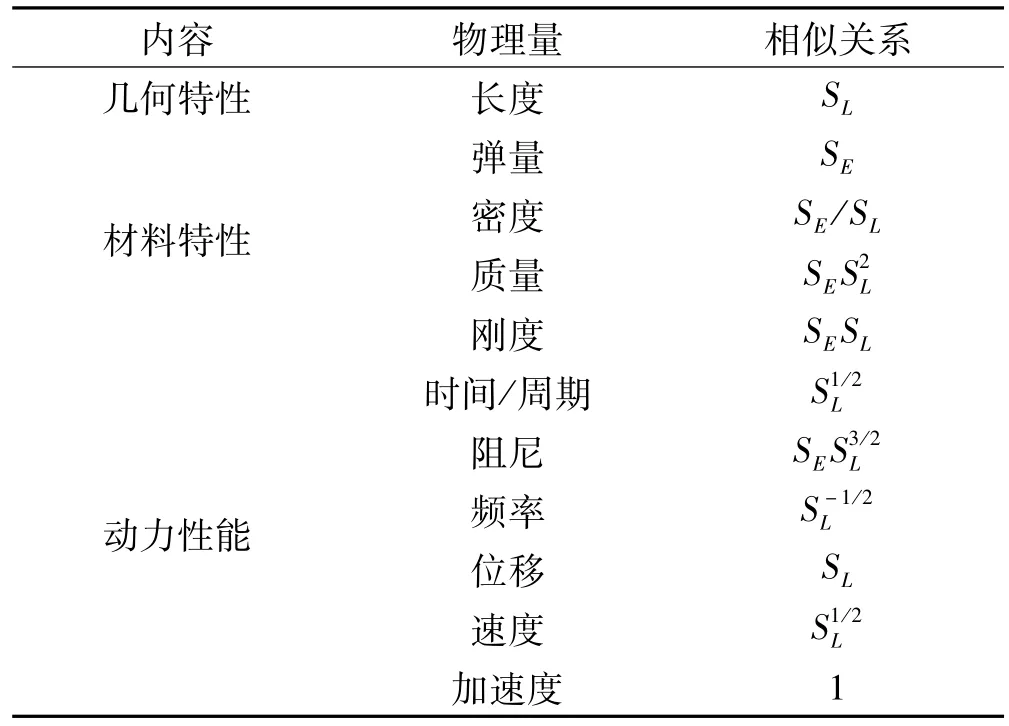
表2 试验模型的动力相似系数Tab．2 Dynamic similitude relations of test model

试验模型为WS－Z30－40标准配置中所带的一个6层铝合金框架模型，模型的相似比为1／10，考虑实际影响，在每层板上配混凝土质量块配重，第1、2、3层上每层布置1．75kg配重块，第4、5层上每层布置1．2 kg配重块，顶层上布置0．6 kg配重块。结构整体模型如图4（a）所示。本试验中取整体结构的顶部两层作为试验子结构，其截面属性、材料特性以及质量块的配重与整体结构顶部两层一致。在子结构模型和台面直接安装橡胶垫－质量块系统来放大结构加速度反应，试验过程中通过调整集中质量块的质量来调节结构的固有频率，两层子结构模型如图4（b）所示。

图4 结构模型Fig．4 Structural model

3.2 整体结构模型地震反应

试验中采用的地震动为EI Centro、Taft和Shw2，加速度峰值调整为3 m／s2。根据相似原理，时间间隔为0．007 s，经时间压缩后的地震加速度时程频率成分的圆频率分别为：El Centro地震动的圆频率f＝4．392 Hz；Taft地震动的圆频率f＝4．1 Hz；Shw2地震动的圆频率f＝3．587 Hz。整体结构模型加速度反应如图5所示。

图5 整体结构模型加速度反应Fig．5 Acceleration responds of whole structural model

3．3 子结构模型地震反应

在子结构模型试验中，首先利用传递函数将原地震动输入变换为新地震动输入，然后通过调节设置在台面上的集中质量块的质量来改变子结构模型的固有频率，在试验过程中采用扫频正弦波激振试验来识别子结构的频率，扫频正弦波的采样频率为100 Hz，扫频时间为300 s，初始频率为1 Hz，结束频率为30 Hz。每条地震动根据设置的质量块质量不同分为三个工况，各工况下所配置的质量块质量如表3所示。

表3 不同工况下的质量块配重Tab．3 Mass counterweight under different working conditions

结构特性及动力响应如表4所示，三种地震动作用下子结构模型加速度反应如图6所示。

3．4 对比分析

将整体结构模型试验和子结构模型试验工况3的顶层加速度反应进行对比，如图7所示。从表4、图6中可以看出：在3条地震波作用下，随着地震动的频率与结构固有频率之比（即ω／ωn）越接近1，结构的加速度响应越大，验证了橡胶垫－质量块系统的放大作用。图7中在工况三作用下，子结构模型和整体结构模型的顶层加速度曲线基本一致，最大值基本相同，但出现最大值的时刻略有偏差，原因可能是由于振动台的精度和时滞所造成的，但整体趋势基本一致，定性的验证了橡胶垫－质量块系统的子结构振动台试验方法的可行性。

表4 结构特性及动力响应Tab．4 Properties and dynamic response of structure

图6 子结构模型加速度反应Fig．6 Acceleration responds of substructural model

图7 整体结构与工况三子结构顶层加速度对比曲线Fig．7 Acceleration responds of top floor between whole structure and substructure with work condition 3

4 结 论

（1）利用时程分析法求解3自由度体系的地震响应，将传递函数与地震响应进行卷积求得新输入地震动，新输入地震动与原输入地震动曲线及两者傅里叶谱曲线吻合较好，验证了传递函数的准确性与适用性。

（2）利用小型振动台分别对6层整体结构，2层带有橡胶垫－质量块系统试验子结构进行了3个工况的振动试验，分别研究不同频率下结构的地震响应。试验表明：随着ω／ωn的比值接近于1，结构的地震响应增大，验证了橡胶垫－质量块系统的放大原理；子结构顶层加速度响应与整体结构顶层加速度响应基本一致，定性地验证了子结构振动台试验方法的可行性，可为高层建筑抗震试验提供研究参考。

［1］Igarashi A， Iemura H， Tanaka H． Development of substructure hybrid shake table test method and application to verification tests of vibration control devices［C］．China-Japan Workshop on Vibration Control and Health Monitoring of Structures and Third Chinese Symposium on Structural Vibration Control．Shanghai，China，2002．

［2］Lee S K， Parka E C， Mina K W etal． Real-time substructuring technique for the shaking table test of upper substructures［J］．Engineering Structures，2007，29（9）：2219－2232．

［3］Kausel E．New Seismic Testing method I：fundamental concepts［J］．Journal of Engineering Mechanics，1998，124（5）：565－570．

［4］Kausel E．New Seismic Testing method II：proof for MDOF system［J］．Journal of Engineering Mechanics．1998，124（5）：571－575．

［5］Reinhorn A M，Sivaselvan M V，Liang Z，et al．Large scale real time dynamic hybrid testing technique-shake Table substructure testing［J］．Advances in Experimental Structural Engineering．Nagoya，Japan．2005：457－464．

［6］Shao X Y，Reinhorn A M，Mettupalayam S．Real time dynamic hybrid testing using force-based substructuring［C］．The8th US National Conference on Earthquake Engineering．San Francisco，California，2006．

［7］保海娥，张自平，程绍革．振动台型混合试验系统试验设备研究［J］．工程抗震与加固改造，2006，28（6）：61－65．BAO Hai-e，ZHANG Zi-ping，CHENG Shao-ge．Testing equipment research on hybrid shaking table test system［J］．Earthquake Resistant Engineering and Retrofitting，2006，28（6）：61－65．

［8］程绍革，马路，赵鹏飞．基于凝聚技术的结构抗震混合试验原理［J］．工程抗震与加固改造，2008，30（2）：62－67．CHENG Shao-ge，MA Lu，ZHAO Peng-fei． Hybrid test method Based on system reduction［J］．Earthquake Resistant Engineering and Retrofitting，2008，30（2）：62－67．

［9］王向英，田石柱．子结构地震模拟振动台混合试验原理与实现［J］．地震工程与工程振动，2009，29（4）：46－52．WANG Xiang-ying，TIAN Shi-zhu．Principle and implementation of the hybrid testing method based on substructure techn iques by using shaking table［J］．Journal of Earthquake Engineering and Engineering Vibration，2009，29（4）：46－52．

［10］李振宝，李晓亮，唐贞云，等．基于振动台的动力子结构试验界面反力获取方法［J］．地震工程与工程振动，2011，31（3）：65－70．LI Zhen-bao，LI Xiao-liang，TANG Zhen-yun．Research on the methods of evaluating reaction force for dynamic substructure experiments using shaking table［J］．Journal of Earthquake Engineering and Engineering Vibration，2011，31（3）：65－70．

［11］JI X D，Fenves G L，Kajiwara K，et al．Seismic damage detection of a full-scale shaking table test structure［J］．Journal of Structure Engineering，2011，137：14－21．

［12］JI X D，Kajiwara K，Nagae T，et al．A substructure shaking table test for reproduction of earthquake responses of high-rise buildings［J］．Earthquake Engineering and Structture Dynamics，2009，38：1381－1399．