基于微型永电磁式涡流阻尼TMD的人行桥模型减振试验研究

汪志昊，华旭刚，陈政清，王 旭，王朝阳

（1.华北水利水电大学 土木与交通学院，郑州 450011；2.湖南大学 风工程试验研究中心，长沙 410082）

调谐质量阻尼器（Tuned Mass Damper，TMD）作为结构振动吸能减振技术中常用形式已在建筑、桥梁结构减振中得到广泛应用［1］，如大跨度桥梁风振［2－7］与人行桥人致振动控制［8－10］。典型桥梁风振控制实例如日本东京湾通道桥用8台竖向TMD附加质量计160 t控制主梁的一、二阶竖弯涡振［2］；巴西 RioNiterói桥利用32台TMD总重70 t进行一阶竖弯涡振控制［3］；美国布朗克斯－白石大桥的涡振与颤振控制［4］，TMD参数不详。除全桥控制外亦有桥梁局部构件的风振控制，如九江桥的刚性吊杆振动控制［6］，南京长江三桥钢塔在施工阶段的振动控制［7］。而人行桥振动控制如英国千禧桥［8］，共安装8台重2.5 t的水平TMD与52台重1～3 t的竖向TMD。

阻尼元件为TMD寿命的决定因素，小型TMD一般采用橡胶等高阻尼材料，大型TMD则采用油阻尼器等。然而橡胶材料存在易老化、刚度与阻尼不易分离的缺点，粘滞阻尼器存在漏油、不易养护等问题，且TMD产品阻尼后期较难调节。结构模型TMD减振实验［11－13］虽对其设计、制作提出更高要求，但现有技术提供的微型TMD过于粗糙，无法实现TMD阻尼与刚度有效分离，较难完成TMD减振实验所需阻尼比参数调整。导致结构模型TMD减振实验只能起到减振效果的定性演示，无法真正为TMD的减振优化设计提供定量参考。

作为极有前途的阻尼形式，电涡流阻尼主要用于航天结构振动控制、汽车减振与刹车及高速列车制动等［14］。其突出优点为：无需接触结构无任何磨损，内无流体不会漏液，刚度与阻尼参数完全分离，阻尼参数后期易于调整。鉴于此，楼梦麟等［15］较早开展外供电式小型电涡流 TMD模型结构减振台试验，汪志昊等［16－17］成功研制出用于人行天桥竖向振动控制的大吨位永磁式电涡流TMD及钢拱桥刚性吊杆风振控制的中型电涡流TMD。本文针对某人行桥模型减振实验，研制出微型永磁式电涡流TMD，并进行性能测试。

1 微型永磁式电涡流TMD设计

1.1 基本参数

据研究成果［9］，某大跨度人行桥横向振动力严重（一阶频率fp与广义质量 m 分别为 0.459 Hz、573.8 t），需安装水平向 TMD减振。设计 TMD需先确定TMD有效质量与结构模态质量之比μ。通常TMD质量比越大，结构减振效果越好；但受安装空间与成本等制约，质量比一般取1%～5%。本文取2%，对应的实桥TMD质量mp为11.5 t。由于人致振动属于稳态激励，故用频率比 fopt与阻尼比 ξopt优 化计算式［18］为

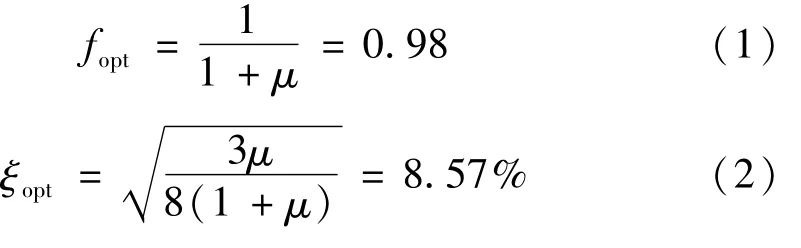
为验证TMD对该桥减振的有效性，先进行人行桥模型减振实验。由西南交通大学风工程试验研究中心制作的全桥气弹模型缩尺比n＝40，试验用TMD质量、目标频率与阻尼比分别为

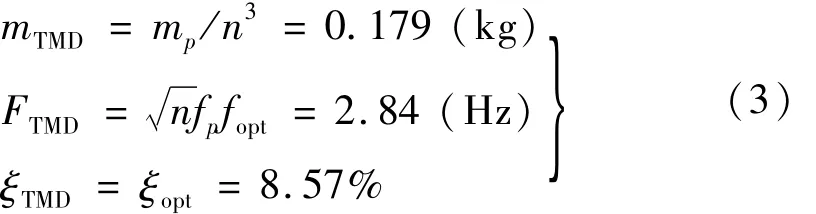
1.2 研制

整体设计构思采用悬臂梁与电涡流阻尼分别作为TMD刚度元件及阻尼元件。即用厚度0.5 mm锯条作为悬臂梁，根部通过夹片与固定的有机玻璃板（安装在控制对象上）相连；将块重0.135 kg长条形钕铁硼（NdFeB）永磁体固定于梁悬臂端，在永磁体下方的有机玻璃板上固定导体铜板，形成TMD的电涡流阻尼机构；TMD有效质量由永磁体、悬臂梁一阶横向弯曲等效模态质量与调节质量块（螺母）组成。调试中的微型永磁式电涡流TMD见图1。该TMD频率可通过改变悬臂梁（锯条）有效长度进行调节，阻尼可通过变化铜板与永磁体间距（在铜板与有机玻璃板中间设置厚度不同垫板）直接改变铜板厚度，或改变永磁体在导体板平面投影面积进行调节。

图1 微型电涡流阻尼TMDFig.1 A tiny eddycurrent damping TMD

2 微型永磁式电涡流TMD性能测试

为说明TMD频率与阻尼的易调性，进行正交变参数测试，即悬臂梁有效长度变化两次：7.5 cm、10.5 cm，导体板厚度变化两次：5 mm、10 mm。试验中用激光位移计记录TMD横向水平位移。悬臂梁有效长度10.5 cm、无附加阻尼的TMD自由振动位移时程曲线见图2，导体铜板厚度5 mm、10 mm对应的TMD自由振动位移时程曲线见图3。

图2 无任何附加阻尼时TMD的自由振动位移时程Fig.2 Free vibration time histories of the TMD’s displacement with no extra damping

所有工况TMD动力参数识别结果见表1。由表1、图2、图3看出，① 微型TMD固有机构阻尼较小可忽略不计；② 附加电涡流阻尼TMD自由振动呈对数衰减规律，一定程度上表明电涡流阻尼的粘滞阻尼特性；③ TMD频率不受电涡流阻尼影响，表明电涡流阻尼无任何附加刚度，可实现微型TMD刚度与阻尼的完全分离；④ 电涡流阻尼装置可大幅提高TMD阻尼比参数，易通过改变导体板厚度进行阻尼比调节。导体板变厚一倍电涡流阻尼比增量大于一倍，此因导体板变厚后其与永磁体间磁场间隙减小，增大导体板的磁感应强度，进而对阻尼比提供额外贡献。

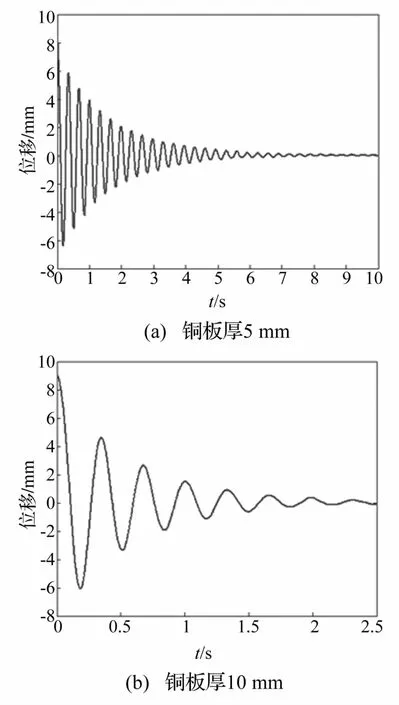
图3 电涡流TMD自由振动位移时程Fig.3 Free vibration time histories of the TMD’s displacement with eddycurrent damping

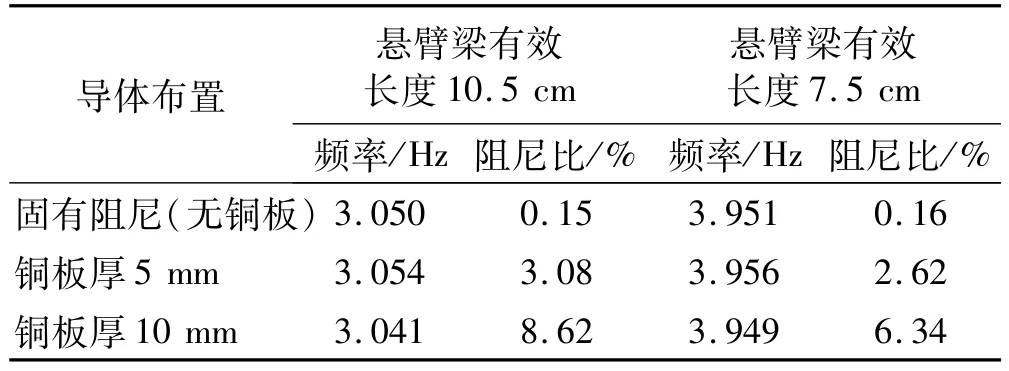
表1 微型电涡流TMD动力参数实验识别结果Tab.1 Identified dynamic parameters of the tiny eddycurrent damping TMD

3 人行桥模型减振效果试验

人行桥模型的TMD减振试验场景见图4。测试系统主要组成为：① 稳态激振装置包括行程、最大出力分别为±5 mm、50 N的JZK－5型激振器（扬州无线电二厂），正弦信号发生器及功率放大器；② 两LC0408T型压电式加速度传感器（频率范围1～18 000 Hz，灵敏度6 Pc／g，质量6 g），分别布置于桥梁主跨跨中横向及TMD永磁体；③ DH5920动态信号测试系统，采样频率200 Hz。实验前准备工作有：① 用自由振动测试方法识别或得人行桥模型一阶横向弯曲振动频率3.25 Hz及阻尼比2.53%；② 据结构模态参数计算TMD参数，考虑TMD附属结构质量（固定悬臂梁及导体板的有机玻璃板、导体板及连接件中螺丝、螺母等）最大达0.2 kg（对应导体板较厚），用式（1）计算TMD频率时μ取4.22%，得 TMD设计频率 3.12 Hz；③ 调试、安装TMD，调试 TMD频率为 3.13 Hz、阻尼比 9.90%，设置较最优阻尼比8.57%稍大的阻尼可在不影响减振效果的同时适当减小TMD最大行程。

实验中采用两种不同的激振方式测试、评估安装TMD的人行桥减振效果：① 直接在桥梁主跨跨中给结构一初始横向位移激励，使人行桥模型做自由衰减振动，对应的TMD及结构绝对加速度时程见图5（a）；②用固定于桥梁主跨跨中横向激振器实现桥梁稳态激励，等结构与TMD响应达稳态后再瞬间释放激励，对应的TMD及结构绝对加速度时程见图5（b）。

图4 人行桥模型的TMD减振试验照片Fig.4 Experimental setup photos for vibration control of a model footbridge with a TMD

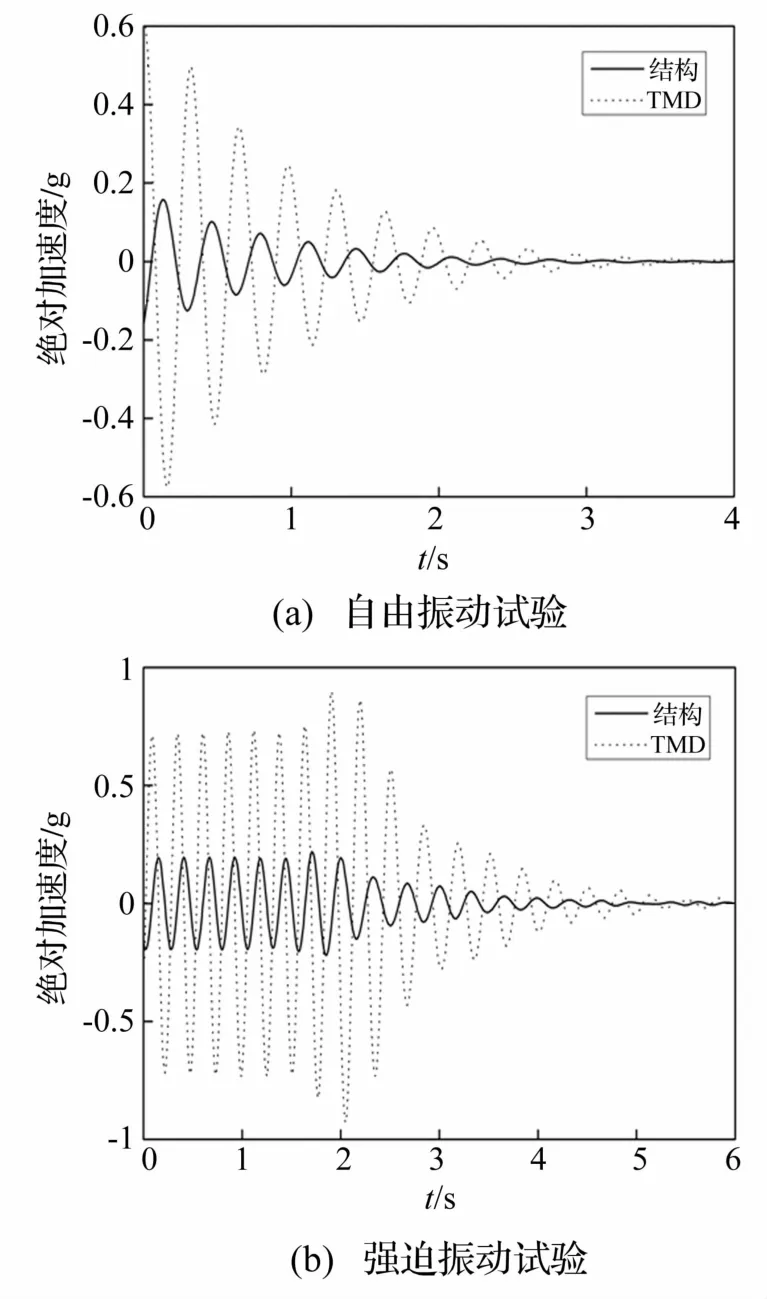
图5 两种不同激振方式下结构与TMD绝对加速度时程Fig.5 Absolute acceleration time histories of both main structure and TMD with two kinds of excitation method

人行桥模型安装TMD后一阶横向弯曲模态参数及强迫振动的动力响应放大倍数测试结果见表2，可见TMD减振效果较好。特别指出：无论自由、强迫振动测试，阻尼比计算均统一取由自由衰减振动第二峰值开始的8个完整周期数据。稳态激励时桥梁绝对、TMD相对加速度幅值分别为 0.2015 g、0.7498 g，若设激振源为频率3.1 Hz、振幅0.5 cm的标准正弦运动，可估算获得人行桥模型主跨跨中、TMD相对位移振幅分别为0.51 cm、1.91 cm，进而获得动力响应放大倍数。

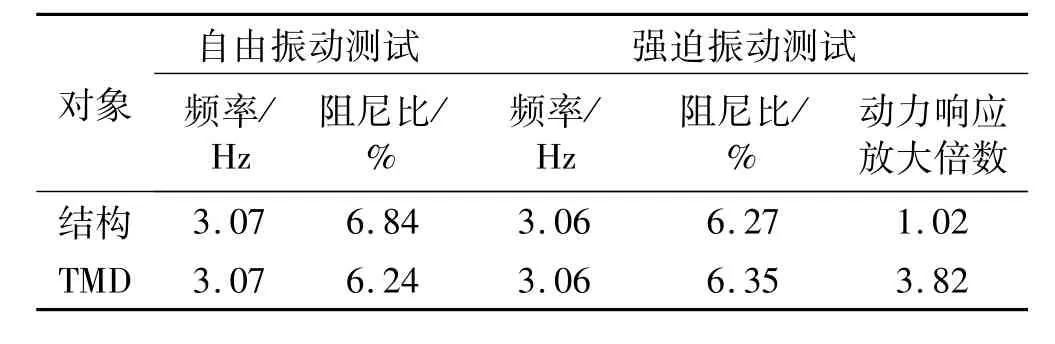
表2 人行桥模型TMD减振结果Tab.2 Vibration control performance of the footbridge with a TMD

用图5数据研究TMD的相对加速度与人行桥模型绝对加速度间相位关系，验证TMD控制效果［18］。研究表明，自由振动测试时，相对人行桥模型绝对加速度TMD相对加速度时间延迟0.13～0.15 s，按试验识别的人行桥模型振动频率3.07 Hz估算可得TMD相位延迟为143.7°～165.8°，且越接近振动后期二者间越接近反相位；强迫振动的稳态响应阶段TMD时间延迟0.07～0.09 s，对应相位延迟77.4°～99.5°（与 TMD最优参数设计的理论相位延迟90°［18］较接近），而自由衰减振动阶段TMD时间延迟0.14～0.17 s，对应相位延迟154.7°～187.9°，与纯自由振动试验测试结果基本相同。

4 结 论

本文通过研制微型永磁式电涡流阻尼TMD，经自身性能测试及人行桥模型减振实验验证TMD的优越性。该微型永磁式电涡流TMD既能确保刚度与阻尼参数的有效分离，亦能实现阻尼参数稳定（阻尼系数与TMD运动位置无关）、简单易调（调整导体铜板厚度可调整阻尼系数），可广泛用于土木工程结构模型TMD减振实验与优化设计。

［1］李春祥，刘艳霞，王肇民.质量阻尼器的发展［J］.力学进展，2003，33（2）：194－206.LI Chunxiang，LIU Yanxia，WANGZhaomin.A review on mass dampers［J］.Advance in Mechanics，2003，33（2）：194－206.

［2］Fujino Y，Yoshida Y.Windinduced vibration and control of TransTokyo Bay Crossing bridge［J］.ASCE Journal of Structural Engineering，2002，128（8）：1012－1025.

［3］Battista R C，Pfeil M S.Control of wind oscillations of RioNiter i bridge，brazil［J］.Proceedings of the ICEStructures and Buildings，2010，163（2）：87－96.

［4］Barelli M，White J，Billington D P.History and aesthetics of the BronxWhitestone bridge［J］.ASCE Journal of Bridge Engineering，2006，11（2）：230－240.

［5］Xing C，Wang H，Li A，et al.Study on windinduced vibration control of a longspan cablestayed bridge using TMDtype counterweight［J］. ASCE Journal of Bridge Engineering，2014，19（1）：141－148.

［6］顾金钧，赵煜澄，邵克华.九江长江大桥应用新型TMD抑制吊杆涡振［J］.土木工程学报，1994，27（3）：3－13.GU Jinjun，ZHAOYucheng，SHAOKehua.Application of new TMD to suppressing vortexshedding vibration of hangers of Jiujiang bridge over Yangtze river［J］.China Civil Engineering Journal，1994，27（3）：3－13.

［7］文永奎，孙利民.大跨度斜拉桥钢塔施工阶段制振用TMD、TLD装置及其性能试验［J］.地震工程与工程振动，2008，28（3）：157－164.WEN Yongkui，SUN Limin.TMD，TLD and performance tests for vibration control of steel tower of large span cablestayed bridge during construction［J］.Journal of Earthquake Engineering and Engineering Vibration，2008，28（3）：157－164.

［8］Roberts T M.Lateral pedestrian excitation of footbridges［J］.ASCE Journal of Bridge Engineering，2005，10（1）：107－112.

［9］陈政清，刘光栋.人行桥的人致振动理论与动力设计［J］.工程力学，2009，26（S2）：148－159.CHEN Zhengqing， LIU Guangdong. Pedestrianinduced vibration theory and dynamic design of footbridges［J］.Engineering Mechanics，2009，26（S2）：148－159.

［10］樊健生，陈宇，聂建国.人行桥的TMD减振优化设计研究［J］.工程力学，2012，29（9）：133－140.FAN Jiansheng，CHEN Yu，NIE Jianguo.Optimum design of tuned mass damper for footbridge［J］.Engineering Mechanics，2012，29（9）：133－140.

［11］王肇民，李宇明，罗烈，等.上海电视塔用TMD进行结构风振控制的风洞试验研究［J］.特种结构，1994，11（3）：14－17.WANG Zhaomin，LI Yuming，LUO Lie，et al.The tunnel test research on wind vibration control of Shanghai TV tower by using TMD ［J］.Journal of Special Structures，1994，11（3）：14－17.

［12］顾明，吴炜，项海帆.大跨桥梁颤振控制的试验研究［J］.同济大学学报（自然科学版），1996，24（2）：124－129.GU Ming，WU Wei，XIANGHaifan.Testing study of flutter control of longspan bridges using tuned mass dampers［J］.Journal of Tongji University（Natural Science Edition），1996，24（2）：124－129.

［13］郭增伟，葛耀君，卢安平.竖弯涡振控制的调谐质量阻尼器TMD参数优化设计［J］.浙江大学学报（工学版），2012，46（1）：8－13.GUO Zengwei， GE Yaojun， LU Anping. Parameter optimization of TMD for vortexinduced vibration control［J］.Journal of Zhejiang University（Engineering Science），2012，46（1）：8－13.

［14］Sodano H A，Bae J S.Eddy current damping in structures［J］.The Shock and Vibration Digest，2004，36（6）：469－478.

［15］楼梦麟，吴和霖，马恒春，等.电磁耗能TMD结构减震效率的振动台试验研究［J］.地震工程与工程振动，2003，23（4）：158－163.LOU Menglin，WU Helin，MA Hengchun，et al.Study on efficiency of electromagnetic energy dissipation TMD to suppress structural vibration by shaking table model test［J］.Journal of Earthquake Engineering and Engineering Vibration，2003，23（4）：158－163.

［16］汪志昊，陈政清.永磁式电涡流调谐质量阻尼器的研制与性能试验［J］.振动工程学报，2013，26（3）：374－379.WANG Zhihao， CHEN Zhengqing. Development and performance tests of an eddycurrent tuned mass damper with permanent magnets［J］.Journal of Vibration Engineering，2013，26（3）：374－379.

［17］汪志昊，陈政清，王建辉.钢拱桥刚性细长吊杆减振用调谐质量阻尼器的试验研究［J］.科学技术与工程，2013，13（19）：131－136.WANG Zhihao， CHEN Zhengqing， WANG Jianhui.Experimental study on tuned mass dampers for vibration control of rigid slender suspenders in steel arch bridges［J］.Science Technology and Engineering，2013，13（19）：131－136.

［18］Soong T T，Dargush G F.Passive energy dissipation systems in structural engineering［M］.New York：John Wiley＆Sons，1997：228－279.