含橡胶轴承轴系振动传递主动控制研究

胡 芳，张志谊，吴天行，华宏星

（1.上海交通大学 机械与动力工程学院，上海 200240；2.武汉理工大学 材料科学与工程学院，武汉 430070）

螺旋桨－轴系是船舶推进系统的重要组成，也是船舶的主要振源之一。螺旋桨脉动力通过轴系向船体结构传递，引起结构振动与噪声，对环境造成影响。在螺旋桨的脉动力中，纵向脉动力主要通过驱动轴和推力轴承引起弹性基础振动，因此，有必要控制纵向脉动力传递，从传递途径上减小驱动轴或推力轴承振动。

在轴上施加集中控制，降低轴的纵向振动，能够抑制脉动力经由轴系向船体结构的传递［1］；在推力轴承上施加分布式控制，降低轴承座的纵向振动，也能抑制振动向船体结构的传递［2］。但是，在轴上或推力轴承上施加控制都面临动态特性随转速变化的问题，有关现象已在试验中得到证明［3－4］。轴系中含有水润滑橡胶轴承和油润滑推力轴承，这类轴承的支承刚度在理论上与流体动力润滑有关，受界面润滑状态影响。轴系支承刚度的这种特性使得由桨－轴－支承构成的系统的动力学建模与控制必须考虑转速因素，在线建模与控制甚至是无模型控制，是解决这类系统振动控制的有效方法［5－6］。螺旋桨－轴系振动具有轴频或叶频调制的特征，主要由螺旋桨的周期性激励引起，而且激励频率、强度随转速变化。对于频率变化的周期性振动控制问题，自适应方法具有较好的适应性，目前常用的方法是在LMS算法基础上构建的系列算法［7－9］。如果使用控制通道模型，必须在不同转速下通过在线辨识建立传递函数或脉冲响应模型，考虑周期性干扰对辨识过程的影响［10］。无模型控制方法将控制通道增益作为变量考虑，通过实时最小化控制误差，自然解决增益的在线辨识问题。目前的无模型控制算法能够对周期干扰进行频率选择控制，需要比较精确的频率估计与窄带滤波以及快速的在线寻优方法，算法的稳定性、收敛性与性能还在深入研究中［11－13］。

通过在线辨识建立控制通道模型能够实现宽带控制，但对于运行轴系，控制通道的在线辨识过程通常受到轴频调制的振动信号的干扰，从而导致控制通道建模精度下降，甚至错误的结果。本文针对特性随转速变化的轴系振动控制问题，讨论控制通道模型的在线辨识方法与轴频调制振动响应的控制方法。首先采用简化的轴系模型揭示轴系振动特性随转速变化的原因，然后基于此模型，通过仿真分析，验证辨识方法与控制方法的有效性，最后在螺旋桨－轴系试验系统中对提出的辨识与控制方法进行检验，进一步验证方法的有效性。

1 轴系振动

含水润滑橡胶轴承的轴系振动与轴颈－轴承界面的接触状态密切相关。由于轴承－轴颈界面始终存在较大的接触力［14］，由摩擦系数决定的界面约束力在静、动之间显著变化，使得支承刚度和阻尼在静、动之间明显改变，从而影响系统的频响特性。为描述这一现象对控制通道动态模型的影响，采用图1所示的简化分析模型，其中轴通过D点、C点轴承与梁连接，AD、BC为刚性杆，kx、ky分别为橡胶轴承的轴向、径向方向刚度，轴与C点通过刚性铰链耦合，F为作用于轴的干扰力，Fa为作用于C点轴承的控制力。在图1中，梁除了允许支承的垂向位移和转角外，还用来模拟具有分布参数的轴系支承基础。

刚度、摩擦力随转速变化规律可用函数关系描述。设Ω为轴转速（rad／s），则橡胶轴承轴向刚度为kx＝k0δ（Ω），其中k0为橡胶轴承轴向最大刚度（Ω＝0）；δ（·）为Dirac函数；界面摩擦力大小随转速变化规律为Nfμsη（Ω），其中 Nf为界面接触力；μs为静摩擦系数，1≥η（Ω）≥0。Ω＞0时Nfμsη（Ω）实际上为轴的轴向振动阻尼力。

设Ds为轴上与D点对应的点，Ds与D分别通过kx，ky在水平、垂直方向耦合。可据界面位移协调关系与力平衡条件用导纳综合方法给出轴与梁的耦合振动方程［15］为

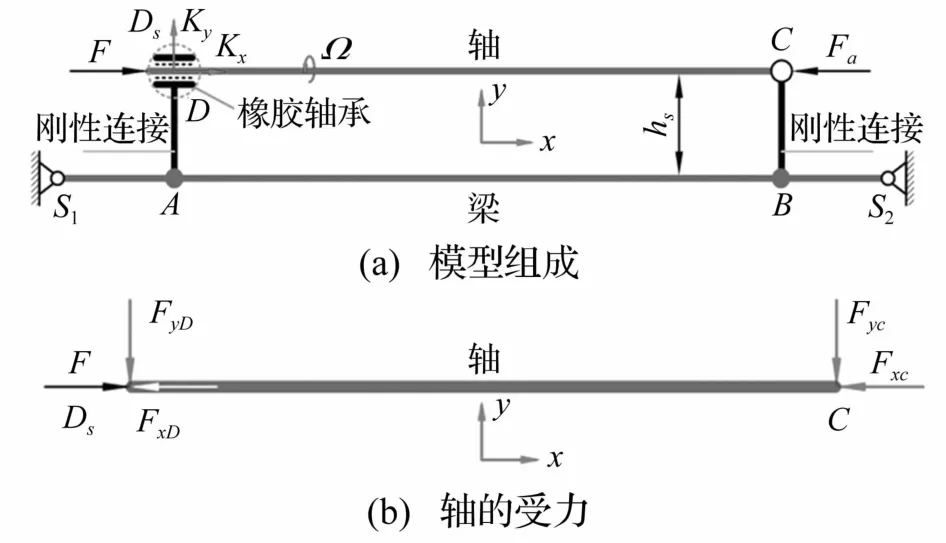
图1 含橡胶轴承轴系振动简化分析模型Fig.1 Simplified model for the vibration analysis of shafting with rubber bearings

yDs＝ky（yDs－yD）Hwf（Ds，Ds）－FyCHwf（Ds，C）（6）式中：Hθm（B，B），Hθm（B，A）分别为 B、A点单位弯矩在B点的转角；Hθm（A，B），Hθm（A，A）依此类推；Hwm（B，B），Hwm（B，A）分别为 B、A点单位弯矩在 B点扰度；Hwm（A，B），Hwm（A，A）依此类推；Hθf（B，B），Hθf（B，A）分别为 B、A点单位力在 B点转角；Hθf（A，B），Hθf（A，A）依此类推；Hwf（B，B），Hwf（B，A）分别为 B、A点单位力在 B点扰度；Hwf（A，B），Hwf（A，A）依此类推；Huf（C，Ds），Huf（C，C）分别为 C、Ds点单位水平力在 C点位移；Huf（Ds，C），Huf（Ds，Ds）依此类推；HWf（C，Ds），HWf（C，C）分别为轴 C、Ds点单位垂向力在 C点扰度；HWf（Ds，C），HWf（Ds，Ds）依此类推；FxD，FyD，FxC，FyC为轴端点所受界面力。

据界面力、位移关系 FxD＝kx（xDs－xD），FyD＝ky（yDs－yD），或 xDs＝FxD／kx＋xD，yDs＝FyD／ky＋yD，可将式（1）～式（6）写成矩阵形式为

据式（7）、（1）可计算由 F，Fa到 xC的频响特性。kx减小时轴与梁的相互约束减弱。由式（7）看出，柔度系数Hθm（A，A）＋Huf（Ds，Ds）＋1／kx增大导致系统部分固有振动频率下降，频响曲线向低频移动，即Ω＞0（kx→0）时频响曲线左移。因此，主动控制需考虑特性变化影响。

激励力F引起结构振动，如果力F与轴转动周期有关，力谱将有转频调制的特征，结构响应亦具有相同特征。设 F（t）＝φ（t）cos（ω0t），其 中 φ（t）＝φ（t＋2π／Ω）为周期 2π／Ω的力幅，ω0为振动频率，则力 F（t）的 Fourier变换 f（ω）为

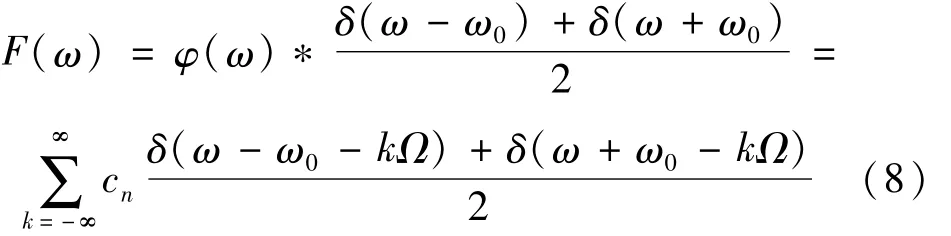
因此，响应亦由一系列谱线构成。

2 控制通道辨识

在给定转速下支承特性是稳定的。由轴－支承构成的系统振动特征几乎不变，考虑作动器动态的控制通道频响亦保持不变。尽管存在与旋转相关的干扰，但仍可用基于线性时不变系统假设的模型辨识方法。先获得含干扰建模频响函数或冲击响应，再通过适当处理剔除与周期干扰有关的特征。对转速变化显著情形，控制通道频响可能需重新辨识。给出建模方法分两阶段：① 先获取含周期干扰的控制通道FIR模型，用LMS递推算法获得控制通道有限冲击响应序列。由于响应中存在周期干扰，FIR序列中亦含虚假特征信息，由于LMS方法将周期振动视为系统小阻尼模态，因此须由初步辨识的FIR序列恢复真正系统有限冲击响应；② 采用子空间滤波方法由FIR序列中识别并去除小阻尼特征与不稳定特征，获得反映系统真实特性的有限冲击响应。

2.1 含周期干扰的控制通道FIR模型

有阻尼系统的脉冲响应能量会逐渐衰减，用有限时间内的脉冲响应即FIR序列能以任意精度近似描述系统动态行为。基于LMS算法的FIR模型辨识原理见图2，其中x（n）为辨识过程激励信号（通常为白噪声）；q（n）为周期干扰，x（n）、q（n）同时激励控制通道H（z）；y（n）为含 H（z）的随机激励响应及周期激励响应；v（n）为测量噪声（宽带随机噪声）；r（n）为FIR模型预测响应；e（n）为实测响应 z（n）与 r（n）之差，即模型辨识误差。

FIR模型系数或 FIR序列 w（n）＝｛w0（n），w1（n），…，wm－1（n）｝T由 LMS算法最小化辨识误差e（n）获得，即

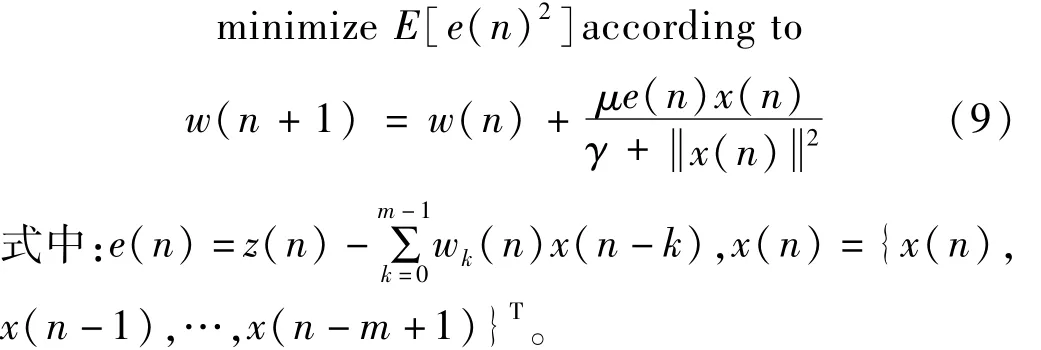
图2（a）可近似等效为图 2（b）。图 2（b）中 G（z）为小阻尼动态系统，其固有频率对应周期干扰q（n）的各阶频率。G（z）在 x（n）作用下响应近似为 H（z）在q（n）作用下响应，即

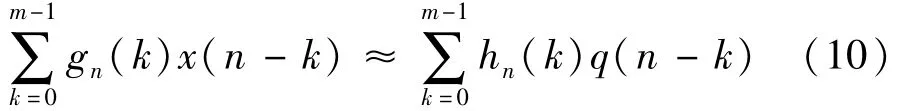
设控制通道 H（z）的冲击响应为 h（n），对应 G（z）的冲击响应为g（n），据图2（b），w（n）＝h（n）＋g（n），去除小阻尼、不稳定模态g（n）即可获得控制通道的FIR。

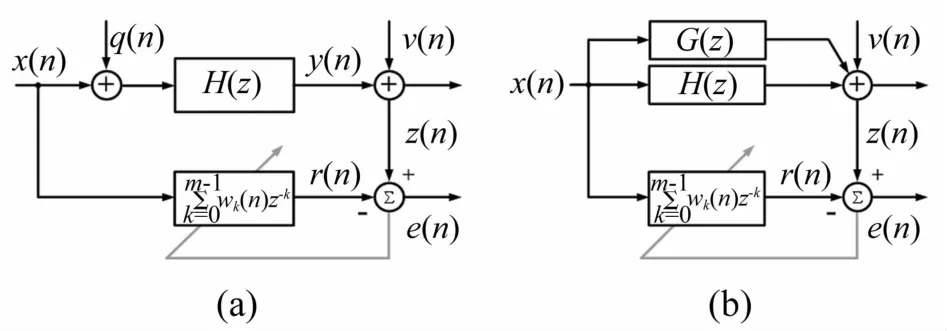
图2 含周期干扰的FIR模型辨识原理Fig.2 Block diagram of the identification of FIR models disturbed by periodical noises

2.2 控制通道FIR模型

从序列w（n）中剔除g（n）的过程分两步。首先由w（n）构造Hankel矩阵，对其进行SVD分解，并根据奇异值的分布确定Hankel矩阵的秩和噪声，进行一次滤波，同时获取对应序列w（n）的特征值。设Hankel矩阵及其SVD分解为

式中：∑1∑2；r＋s＜m，∑1可决定矩阵 Hw的秩，由U1可求得含特征信息矩阵［16］为

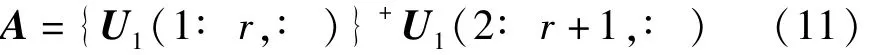
式中：U1（1∶r，∶）为矩阵 U1的第 1－r行子矩阵；（1∶r，∶）为U1（1∶r，∶）的广义逆矩阵；U1（2∶r＋1，∶）为矩阵U1的第2－r＋1行子矩阵。

3 自适应控制

周期干扰控制可以采用Filteredx LMS自适应谐波抵消方法，原理见图3，其中H槇（z）为辨识得到的控制通道模型，d（n）为干扰信号，y（n）为控制通道输出，e（n）为控制误差，e（n）＝d（n）－y（n），d（n）为观测的干扰信号，控制器W（z）为FIR滤波器，其后跟随饱和单元，以限制控制器的输出幅值。控制器W（z）的系数θ＝｛θ0，θ1，…，θα－1｝T（α为正整数）的调整公式［17］为

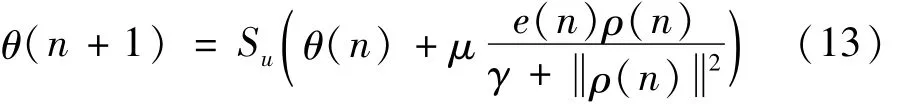
式中：ρ（n）＝｛z（n），z（n－1），…，z（n＋1－α）｝T；Su为Sigmoid函数 S的一阶导数；0＜μ＜1，γ＞0。

控制信号 u（n）＝S（θT（n）r（n）），其中 r（n）＝｛（n），（n－1），…（n＋1－α）｝T。图3中干扰信号d（n）作为参考信号，由于（n）＝d（n）－（H槇（z）－H（z））u（z）（z）＝H（z）时，（n）＝d（n），因此FIR模型的辨识精度对保证控制效果非常重要。

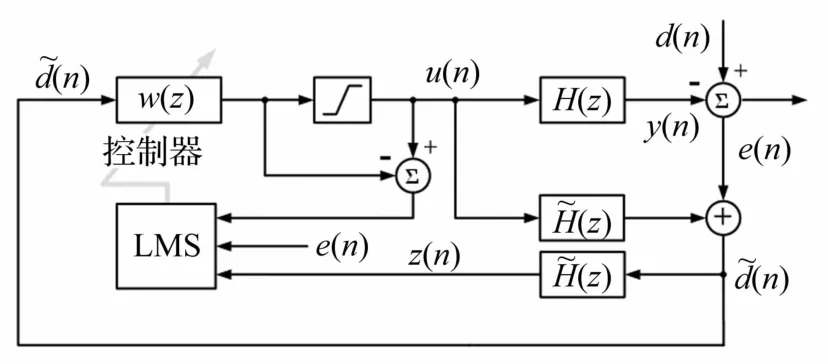
图3 周期干扰的自适应控制原理图Fig.3 Block diagram of the adaptive control of periodical disturbances

4 频响特性变化

4.1 算例

以图1中的模型为对象分析轴承水平刚度变化对频响特性的影响。图中S1S2与CD均为直径0.027 m的圆截面梁，S1A的长度为0.2 m，S2B的长度为0.1 m，CD的长度为 0.6 m，材料弹性模量为 2.1×1011N／m2，泊松比为 0.3，密度为 7 800 kg／m3，AD、BC为无质量刚性杆，hs＝0.1 m，ky＝107N／m，kx＝5×106，104，103，0 N／m。按式（7）计算固有频率，结果列于表1中。从表中可看到，模型的固有频率随kx减小而下降，但在kx降到一定值后几乎不再改变。

因此，当轴承刚度按kx＝k0δ（Ω）规律变化时，频响特性会有显著不同。计算C点原点频响（其中模态阻尼比取10%）结果见图4。由图4看出，控制轴在转速Ω＞0时的振动，控制模型则不能采用转速Ω＝0时对应模型，否则幅值与相位误差会引起控制稳定性问题。

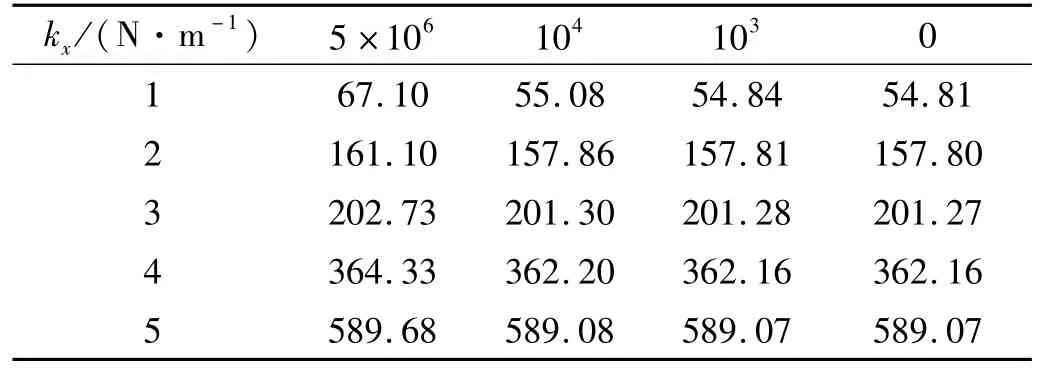
表1 不同支承刚度下的固有频率（Hz）Tab.1 Natural frequencies associated with different bearing stiffness

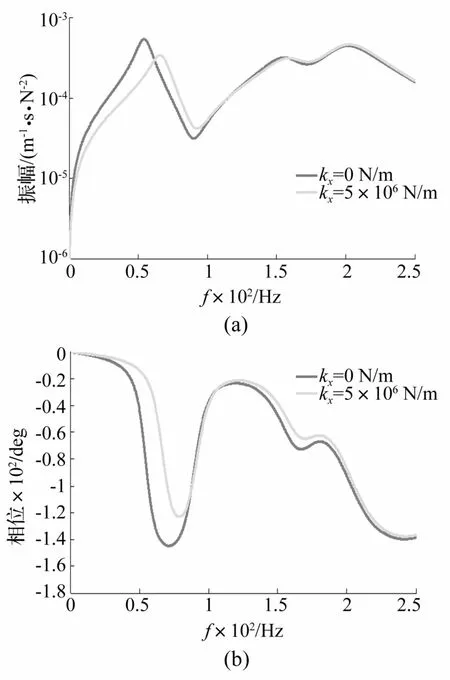
图4 不同刚度下的幅频与相频特性Fig.4 Magnitude／phase－frequency characteristics corresponding to different stiffness

42 实例

螺旋桨－轴系试验系统构成如图5所示，对应的试验系统实物见图6。螺旋桨置于水箱中，运转时产生轴向推力（含脉动成份），并通过轴作用于推力轴承，进而引起轴承支撑结构（板）振动。轴的支承除了推力轴承，还包括水润滑橡胶轴承，该轴承与轴之间的静摩擦力使得轴－轴承界面在振动状态无滑动。惯性式作动器安装于推力轴承处，用于抑制推力轴承座的水平振动。

在推力轴承处施加水平激励力（随机激励），同时测量推力轴承的水平振动，可以得到推力轴承处的控制通道频响函数。图7为推力轴承在不同轴转速下的频响曲线（由激励电压到振动加速度），其中15 Hz附近的共振频率对应作动器固有频率（不随转速变化），由图可见，频响曲线在轴启动后明显左移，而且系统阻尼有所增大（支承界面的滑动摩擦阻尼起作用），但是幅频、相频特性随转速增加的变化不再明显。此外，在轴转动时，测试得到的幅频曲线中还存在间距为转频的谱线，如150 r／min对应间距为2.5 Hz的谱线、300 r／min对应间距为5 Hz的谱线，这些谱线由转速调制周期振动叠加形成，实际上对频响特性测试造成干扰。

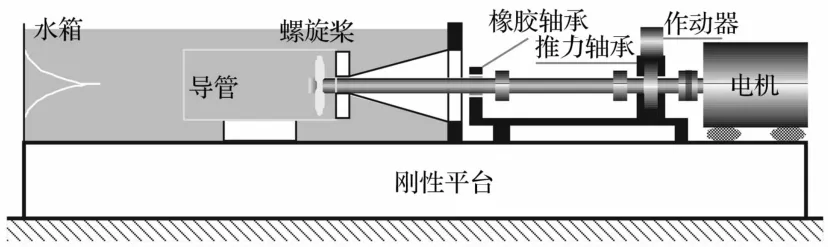
图5 螺旋桨轴系试验台示意图Fig.5 Schematic of the experimental propellershafting system

图6 试验系统Fig.6 Photo of the experimental system

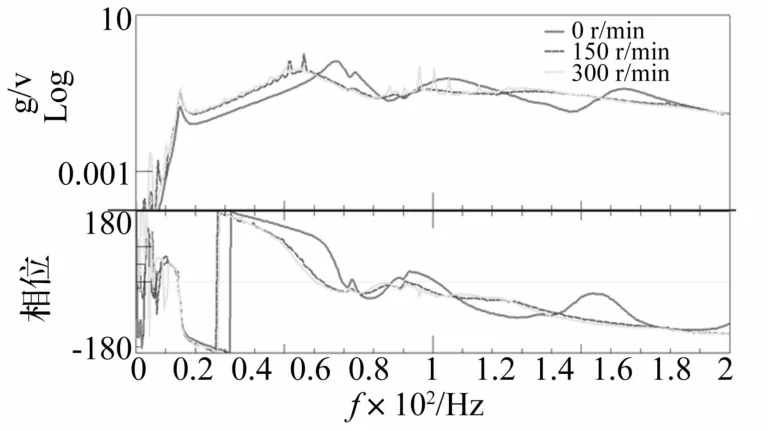
图7 含周期振动干扰的不同转速下的频响曲线Fig.7 Frequency response curves with periodical disturbances measured at different speeds

5 振动响应控制

5.1 仿真研究

以图1所示系统为研究对象，取kx＝0 N／m。首先计算C点原点频响函数，并通过频响函数拟合得到对应的有理多项式模型或ARMA模型，以便计算C点在一定激励下的响应；其次，根据图2的原理，在无干扰条件下得到ARMA模型对应的的脉冲响应（采样频率为1 000 Hz），结果如图8所示；然后考虑随机激励响应与周期干扰同时存在时的脉冲响应辨识，采用在区间［－0.5，0.5］上均匀分布的随机激励，并将ARMA模型在随机激励下的响应与幅值调制的周期振动0.05（0.5＋0.5sin（8πt）sin（160πt）进行叠加，依据图 2的原理对脉冲响应进行辨识，结果示于图8（a）。由图可见，从污染信号中直接辨识的脉冲响应存在不衰减的周期振荡成份。为了从直接辨识的脉冲序列中恢复真实的序列，使用滤波方法滤除原始序列中隐含的不稳定模态和小阻尼模态，最终得到的冲击响应序列与真实的脉冲响应序列几乎一致，如图8（b）所示。

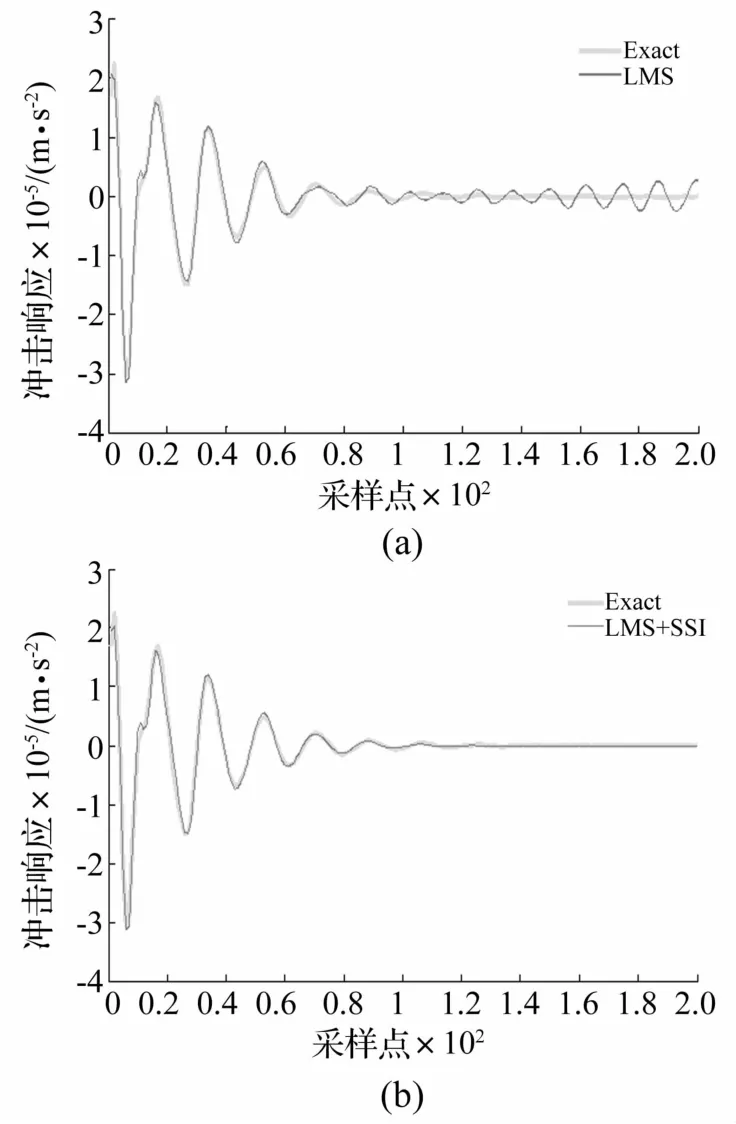
图8 辨识前后单位脉冲响应Fig.8 Identified impulse responses before／after noise elimination

根据图3的控制原理，使用恢复的脉冲响应序列即可对调制的周期振动进行控制。假设作用于C点的周期激励力为（0.5＋0.5sin（8πt）sin（160πt），仍然使用对应C点频响的ARMA模型计算响应，同时采用观测的干扰信号作为Filteredx LMS控制算法的参考输入。观测的干扰信号等于控制信号和辨识的脉冲响应的卷积再与控制误差的叠加，它包含了稳定的干扰源信息。控制仿真结果如图9所示，可见主要峰值在控制后均得到抑制。

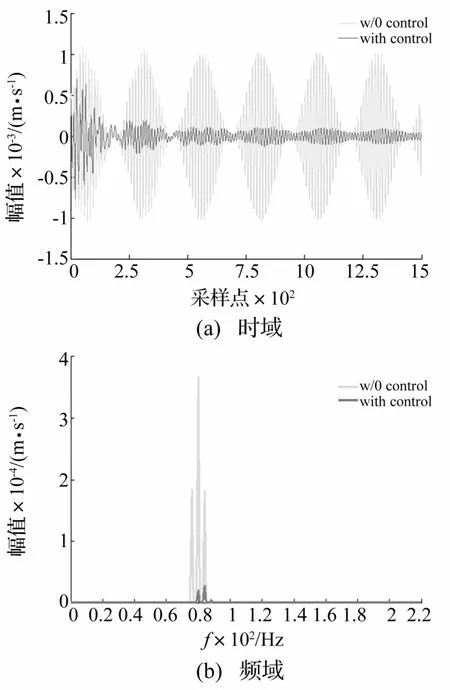
图9 控制仿真结果Fig.9 Simulation resultsof the active control

图10 不同转速下推力轴承座振动控制效果Fig.10 Comparison of vibrationat the thrust bearing before／after control

5.2 控制试验

实际控制效果以图5、图6所示的螺旋桨－轴系试验台进行验证。试验所用作动器为惯性式电磁作动器，其惯性体的悬浮频率为15 Hz。控制系统为内嵌NIPCIe数据采集卡的工控机，传感器为振动加速度计，其电荷输出经电荷放大器转化为DAQ卡可以接受的电压信号。控制系统的采样频率为1000 Hz，前置滤波器带宽为100 Hz。采用自功率谱描述控制前后的振动，图10（a、b、c）为不同转速下的控制效果。由图10可见，尽管不同转速下的调制程度不一样，但各主要振动幅值都能得到较大幅度衰减。实际上，只要脉冲响应准确获取，这种控制效果是由LMS算法保证的。需要说明的是，控制采用的脉冲响应是在180 r／min转速下辨识获得的。显然，根据控制结果，该脉冲响用于其它转速也是有效的。这种性质除了与算法的鲁棒性有关，还与图7所示的频响特性有关，即较高转速下的频响特性几乎一致。因此，本文方法对螺旋桨－轴系系统具有良好的适用性。

6 结 论

橡胶轴承使轴系自由振动频率随转速变化，从而使得不同转速下的控制通道模型必须通过在线辨识获得，然而轴系运转时的激励会导致转速调制的振动响应，这个干扰会影响控制通道模型的在线辨识精度。

针对模型在线辨识与振动控制问题，本文提出的基于子空间特征提取的滤波方法能够恢复控制通道的脉冲响应，使得内含干扰重构的Filteredx LMS控制方法能够有效抑制转速调制的振动响应。控制方法的有效性在螺旋桨－轴系试验系统上得到了验证。

本文提出的物理模型从原理上解释了橡胶轴承约束刚度变化对频响特性的影响，说明界面摩擦力发生显著变化，通过结构内部的位移约束变化使得摩擦副界面约束刚度在静、动之间发生突变，导致系统自由振动频率发生明显漂移。

［1］Cao Yiping，Zhang Wenping.Using dynamic absorbers to reduce underwater structural noise due to longitudinal vibration of shafting［J］.Journal of Harbin Engineering University，2007，28（7）：747－751.

［2］Merz S.Passive and active control of the sound radiated by a submerged vessel due to propeller forces［D］.Thesis of University of New South Wales，Sydney，Australia，2010.

［3］Zhang Z Y，Hu F，Chen Y，et al.Active vibration control of a shafthull systemexperiment［C］.Proceedings of the 19th International Congress on Sound and Vibration，2012：774－781.

［4］Pan J，Farag N，Lin T，et al.Propeller induced structural vibration through the thrust bearing［C］.Proceedings of the Annual Conference of the Australian Acoustical Society，2002：390－399.

［5］Hu F，Chen Y，Zhang Z Y，et al.Tonal vibration suppression with a modelfree control method［J］.Journal of Engineering for the Maritime Environment，2012，226（4）：360－370.

［6］Zhang M，Lan H，Ser W.Crossupdated active noise control system withonline secondary path modeling［J］.IEEE Transactions on Speech and Audio Processing，2001，9（5）：598－602.

［7］Kim B，Washington G N，Singh R.Control of modulated vibration using an enhanced adaptive filtering algorithm based on modelbased approach［J］.Journal of Sound and Vibration，2012，331：4101－4114.

［8］Bohn C，Cortabarria A，Hartel V，et al.Active control of engineinduced vibrations inautomotive vehicles using disturbance observer gain scheduling［J］.Control Engineering Practice，2004，12：1029－1039.

［9］Hkansson L，Claesson I，Sturesson P O.Adaptive feedback control of machinetool vibration based on the filteredx LMS algorithm［J］.International Journal of Low Frequency Noise，Vibration and Active Control，1998，17（4）：199－213.

［10］Sane H S，Venugopal R，Bernstein D S.Disturbance rejection using selftuning ARMARKOV adaptive control with simultaneous identification［J］.IEEE Transactions on Control Systems Technology，2001，9（1）：101－106.

［11］Niedzwiecki M，Meller M.A new approach to active noise and vibration controlpart I：theknown frequency case［J］.IEEE Trans.Signal Processing，2009，57（9）：3373－3386.

［12］Niedzwiecki M，Meller M.A new approach to active noise and vibration controlpart II：theunknown frequency case［J］.IEEE Trans.Signal Processing，2010，57（9）：3387－3398.

［13］Pigg S，Bodson M.Adaptive algorithms for the rejection of sinusoidaldisturbances acting on unknown plants［J］.IEEE Transactions on Control Systems Technology，2010，18（4）：822－836.

［14］Zhang Z Y，Chen F，Hua H X.Research on the coupling between torsional and lateral vibrations in propellershaft system with friction［J］.Chinese Journal of Mechanical Engineering，2013，49（6）：74－80.

［15］Zhang Z Y，Rustighi E，Chen Y，et al.Active control of the longitudinallateral vibration of a shaftplate coupled system［J］.Journal of Vibration and Acoustics，2012，134（6）：061002.1－061002.11.

［16］Fan J，Zhang Z Y，Hua H X.Data processing in subspace identification and modal parameter identification of an arch bridge［J］.Mechanical Systems and Signal Processing，2007，21（4）：1674－1689.

［17］Zhang Z Y，Hu F，Wang J.On saturation suppression in adaptive vibration control［J］.Journal of Sound and Vibration，2010，329：1209－1214.