基于低秩Hankel矩阵逼近的模态参数识别方法

包兴先，李昌良，刘志慧

（中国石油大学（华东）石油工程学院，山东 青岛 266580）

模态参数识别技术广泛应用于工程领域，已成为解决各类工程问题的重要手段。传统模态参数识别方法建立在已知系统输入、输出基础上，据输入输出信息利用实验模态分析获得系统模态参数。但工程实际中激励信号较难获得，通常只获得含噪声的响应信号，因此基于输出响应的模态参数识别技术颇受重视。受测量噪声影响，识别结果通常含虚假模态，如何辨识并剔除虚假模态成为参数识别过程关键。目前模态参数识别通常为计算用模型阶次高于真实模型阶次，引入“噪声模态”［1］。为区分真实、虚假模态大多用稳定图方法［2］。稳定图可表示模态参数与模型阶次关系，理论上随模型阶次的增加，真实模态参数趋于稳定而虚假模态不会，但实际上识别结果中真实模态参数也存在不稳定性，导致稳定图法失效。尤其随模型阶次的升高，虚假模态易趋于稳定，用稳定图较难正确识别结构真实模态参数［3－4］。尤其信噪比较低时区分大量虚假、真实模态更困难。为准确确定模型阶次，基于奇异值分解方法［4－7］一般可通过观察确定奇异值曲线突变点对应的奇异值个数即模型阶次。王树青等［8］提出基于奇异值相对变化率方法，引入量化模型阶次指标，以该指标最大值对应的阶次作为模型阶次。对输出响应信号降噪，基于奇异值分解方法应用最广。研究表明，奇异值分解具有理想的去相关特性，基于奇异值分解的信号分析方法可对信号进行重构，能较好从背景噪声中分离出有用信号［9］；但利用奇异值分解的降噪方法通常只能进行一次截断奇异值分解（TSVD）［10－12］，不能获得最佳降噪效果。理论上对响应信号降噪技术，属线性数学中矩阵低秩逼近（Low Rank Approximation）范畴，通过获得Frobenius范数意义的最佳逼近矩阵降低噪声［13］。低秩逼近可解决信号过程及图像增强中减噪问题。所谓结构低秩逼近指保持矩阵结构情况下对其秩进行约束。本文提出低秩Hankel矩阵逼近方法降低响应信号中噪声干扰。利用结构测量脉冲响应信号构造Hankel矩阵，并进行低秩逼近计算后获得降噪信号，并用其进行模态参数识别。通过数值算例研究测量噪声、矩阵维数等对低秩Hankel矩阵逼近方法影响，利用某悬臂梁实验数据验证本方法的有效性。

1 低秩Hankel矩阵逼近方法

1.1 Hankel矩阵及奇异值分解

一个N自由度动力系统脉冲响应函数可表示为

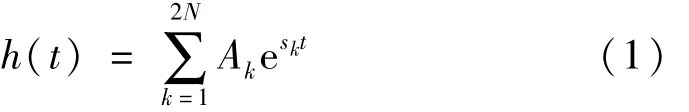
实测脉冲响应函数h（t）中含未知的M阶模态，并以采样间隔Δt表示成离散形式时，式（1）可表示为

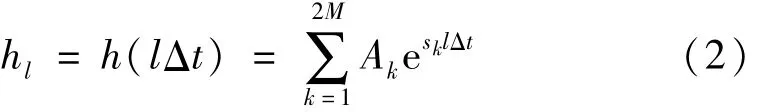
式中：M≤N；l＝0，1，2，…。

用该实测脉冲响应信号hl构建m×n维Hankel矩阵，得

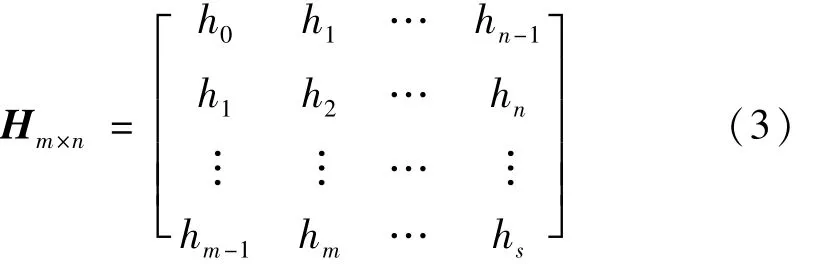
式中：m，n为 Hankel矩阵行、列数，m，n≥2M；s＝m＋n－2。

对Hm×n进行奇异值分解，得

式中：上标“T”表示矩阵转置；U，V为正交矩阵；∑为对角矩阵，对角元素为降序排列的奇异值。而∑可分解为r个非零奇异值子矩阵∑r及几个零子矩阵，即

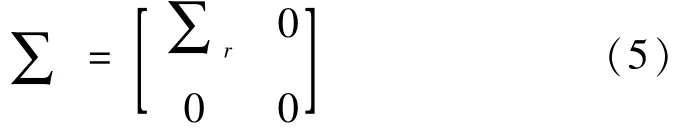
式（5）表明矩阵Hm×n的秩为r。理论上超出矩阵秩的奇异值应为零。实测信号因随机噪声影响，奇异值并不等于零，但会变得很小［14］。

1.2 低秩逼近

当实测脉冲响应序列hl受随机噪声干扰时可写为

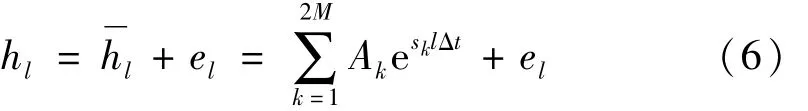
式中：l，el为真实信号及噪声。

理论上，由含噪信号hl构建的Hankel矩阵H可分为两部分，即

式中：为真实信号构建的Hankel矩阵；E为噪声矩阵。已证明，若信号l包含M阶模态，则矩阵的秩等于2M［14］。即矩阵的秩即为模型阶次，为信号中包含模态数的两倍。

低秩Hankel矩阵逼近降噪方法的基本思想为：基于H获，即通过与H最接近的Hankel矩阵＾（秩为2M）逼近，使矩阵H与之差的 Frobenius范数最小。具体步骤为：① 对Hankel矩阵H进行截断奇异值分解，即H＝U∑VT，基于确定的模型阶次，即矩阵的秩r获得获得低秩逼近矩阵。此时＾不满足Hankel矩阵形式。② 将矩阵A＾中各元素由其所在反对角线上元素的数学平均值代替，获得满足 Hankel形式的矩阵 H＾。H＾的秩不为 r。交替迭代步骤①、②，直至满足收敛标准。

1.3 关键点

对含噪信号用低秩Hankel矩阵逼近降噪的两关键点在于如何确定Hankel矩阵维数即m，n及如何保留由真实信号产生的奇异值分离阶数，即如何确定模型阶次r。本文通过数值算例研究矩阵维数选择对计算效率、降噪效果影响规律，并基于奇异值分解方法确定模型阶次。

2 数值算例

2.1 数据模拟

建立5自由度质量－弹簧－阻尼系统数值模型见图1。单元质量、刚度、阻尼系数分别为 mn＝50 kg，kn＝2.9×107N／m，cn＝1 000 N·s／m。经特征值分析，得模态频率理论值为 34.499 Hz，100.70 Hz，158.730 Hz，203.880 Hz，232.520 Hz；模态阻尼比的理论值为 0.003 737 4，0.010 909，0.017 197，0.022 092，0.025 198。

图1 五自由度质量－弹簧－阻尼系统Fig.1 A 5－DOF massspringdashpot system

在任一自由度输入单位脉冲激励可得任一自由度输出的脉冲响应函数。用Matlab编制程序可得25个脉冲响应函数。本例采用第1自由度输入、第1自由度输出的脉冲响应函数，1 024个采样点，采样频率500 Hz，经傅里叶变换可得频率响应函数。通过对精确（不含噪声）脉冲响应函数叠加高斯白噪声模拟含噪的脉冲响应函数。噪声水平用百分比定量描述，该百分比定义为白噪声标准差与精确信号标准差之比。精确信号与含5%、20%噪声信号频率响应函数见图2，图中5个峰值分别对应5阶模态频率，第5阶模态（频率232.520 Hz）相对较弱，易受噪声干扰。

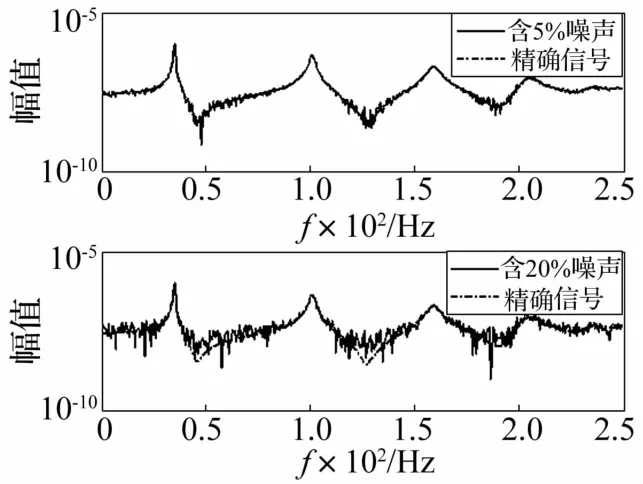
图2 精确信号与含5%、20%噪声信号对比Fig.2 The comparison of noise free signal and signal with 5%and 20%noise

2.2 确定模型阶次

用基于奇异值的相对变化率［8］确定模型阶次。利用结构脉冲响应信号构造Hankel矩阵，进行奇异值分解后计算相邻奇异值相对变化率。变化率最大值即为对应模型的阶次。不含噪声情况下对1 024个采样点构建Hankel矩阵。多次计算发现矩阵维数只要满足行数、列数大于模型阶次即可，即m，n＞10。故构建Hankel矩阵H513×512，并进行奇异值分解，计算奇异值相对变化率－模型阶次指标，见图3（a）。很明显，模型阶次指标最大值对应10阶。对含5%、20%噪声脉冲响应信号，模型阶次计算结果见图3（b）、（c）。可以看出，随噪声增强，模型阶次最大值指标减小。5%噪声时可确定模型阶次为10；20%噪声时模型阶次为8，说明信号中某阶模态被噪声湮没。由于第5阶模态对脉冲响应贡献较小，更易受噪声影响。噪声严重时第5阶模态完全被噪声湮没，故模型阶次由10降为8。

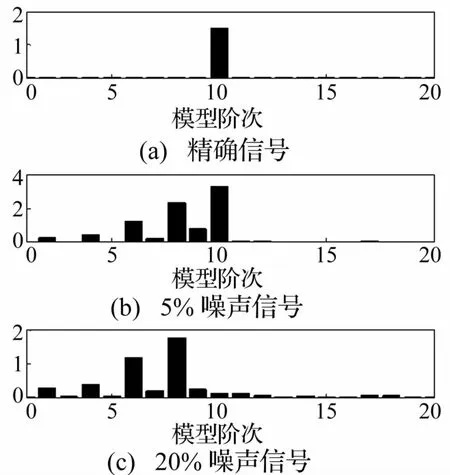
图3 不同噪声的模型阶次指标Fig.3 Model order indicators with different noise level

2.3 信号降噪

含噪信号确定模型阶次后采用低秩Hankel矩阵逼近方法进行降噪的另个关键点在于如何确定矩阵的维数。以含5%噪声信号为例，理论上对秩约束为10的Hankel矩阵低秩逼近计算，矩阵维数只需满足行数、列数大于10。因此矩阵最小维数为H1014×11，最大维数为H513×512。当选择矩阵最小维数n＝11（n为矩阵列数）时，用低秩 Hankel矩阵逼近方法分别经100、1 000、10 000次迭代，获得降噪效果见图4。由图4看出，尽管低频区噪声可有效消除掉，但高频区噪声即使经10 000次迭代仍明显存在。而采用矩阵的最大维数n＝512时，仅经2次迭代即达较好降噪效果，见图5。

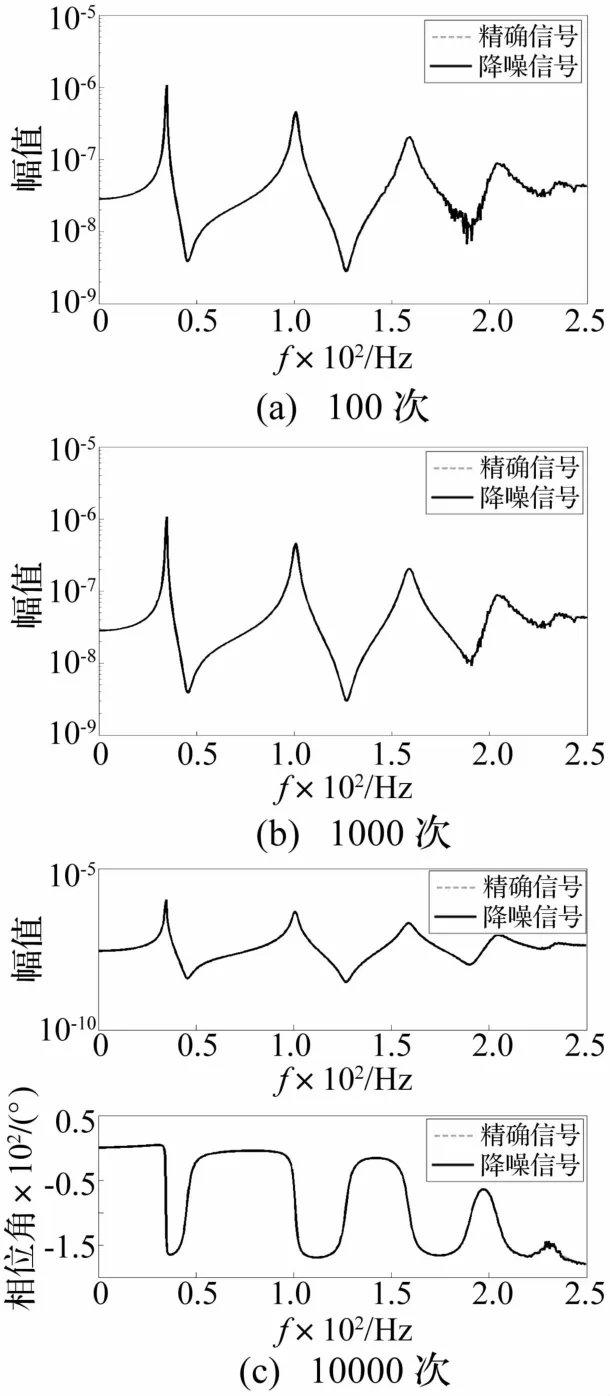
图4 n＝11时经不同迭代次数后降噪效果Fig.4 Performance of noise elimination for theHankel matrix with n＝11

为量化降噪效果，引入作为评价指标。其中F，F＾分别为精确及降噪后频响函数，2代表Frobenius范数。实际上α在数值上等于已定义的噪声水平，含5%噪声信号的α值为0.05。对应不同维数矩阵（n＝11、30、100、512），α与迭代次数关系见图6。由图6看出，n＝512时只需2次迭代α即达到水平渐近线值0.007；n＝11时即使经10 000次迭代α为0.01，仍大于n＝512时经1次迭代的α值；n＝512时降噪效果最好，n＝11时降噪效果最差。

用同一台计算机，n＝11、512的计算用时与迭代次数比较见表1。由表1看出，n＝512的单次迭代用时为n＝11的30倍，达到收敛所需迭代次数n＝11是n＝512的约10000倍。因此，n＝512的计算效率更高。需说明的是，图6中未列出其它维数矩阵降噪情况。实际上，经多次计算发现，约n＝300时曲线与n＝512的曲线几乎重合，考虑计算用时，n＝300的计算效率更高，可认为n＝300为更好选择；但为降噪算法应用简便，对任意个数的脉冲响应信号，仍建议选方阵或接近方阵的Hankel矩阵形式。

图5 n＝512时2次迭代后降噪效果Fig.5 Performance of noise elimination for the Hankel matrix with n＝512 after 2 iterations

图6 不同维数矩阵α与迭代次数关系Fig.6αagainst the number of iterations for Hankel matrices

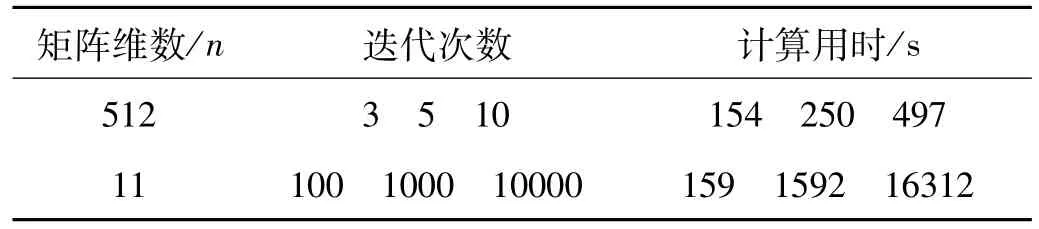
表1 不同维数Hankel矩阵计算效率比较Tab.1 Comparison of the computational time for Hankel matrices

2.4 模态参数识别

对降噪后脉冲响应信号采用单参考点复指数法进行模态参数识别［1］。识别的模态频率、阻尼比分别见表2、表3。与理论值、含噪信号识别值对比看出，采用降噪后信号识别的模态频率、阻尼比与理论值非常接近，模态频率相对误差不超过0.1%，阻尼比前4阶最大相对误差为2.725%，第5阶阻尼比识别误差较大，因第5阶模态贡献最小，最易受噪声影响，含噪信号无法识别第5阶模态频率及阻尼比。前4阶识别结果相对误差亦较大。

表2 用降噪信号与含5%噪声信号识别模态频率 （Hz）Tab.2 The estimated modal frequencies from the filtered and 5%corrupted signals（Hz）

表3 用降噪信号与含5%噪声信号识别阻尼比Tab.3 The estimated damping ratios from the filtered and 5%corrupted signals

2.5 含20%噪声信号

由以上知，信号中第5阶模态完全被噪声湮没，确定模型阶次为8，构建Hankel矩阵H513×512，通过秩约束为8的矩阵低秩逼近计算获得降噪信号；但第5阶模态经降噪处理后丢失。通过对降噪及含噪信号分别进行模态识别，结果见表4、表5。对比二表发现，采用降噪信号识别的前4阶模态频率与理论值较接近，模态频率相对误差范围为0～0.358%，阻尼比相对误差范围1.109%～8.705%。相反，采用含噪信号识别的模态频率及阻尼比的相对误差均较大。

表4 用降噪信号及含20%噪声信号识别的模态频率 （Hz）Tab.4 The estimated modal frequencies from the filtered and 20%corrupted signals（Hz）

表5 用降噪信号及含20%噪声信号识别阻尼比Tab.5 The estimated damping ratios from the filtered and 20%corrupted signals

3 悬臂梁模型试验

为验证本文所提方法的有效性，用悬臂梁进行冲击实验。布置传感器测量振动响应，见图7。采样频率400 Hz。采用上端两传感器测量脉冲响应为例，说明本方法的应用步骤。对两组响应各取512个数据点分别构建Hankel矩阵H257×256，通过计算模型阶次指标得两组响应信号模型阶次均为6，见图8。分别对基于秩约束为6的两矩阵H257×256进行低秩逼近计算，获得降噪信号，见图9。由图9看出，实测信号中毛刺（噪声）已被去除。对降噪信号进行模态参数识别，并与实测信号识别结果对比，见表6、表7。尽管无法获得实验模型真实模态参数，但可通过对比不同信号识别结果的一致性评价。由降噪信号识别的模态参数一致性较好，其中 3阶模态频率相对误差分别为 0.001%，0.002%，0.007%；阻尼比相对误差分别为 0.018%，0.060%，0.553%，均远小于实测信号识别值的相对误差。

图7 悬臂梁物理模型及传感器布置Fig.7 A cantilever beam experimental setup and one closeup accelerometer

图8 两组信号模型阶次指标Fig.8 Model order indicators for measured signals at two locations

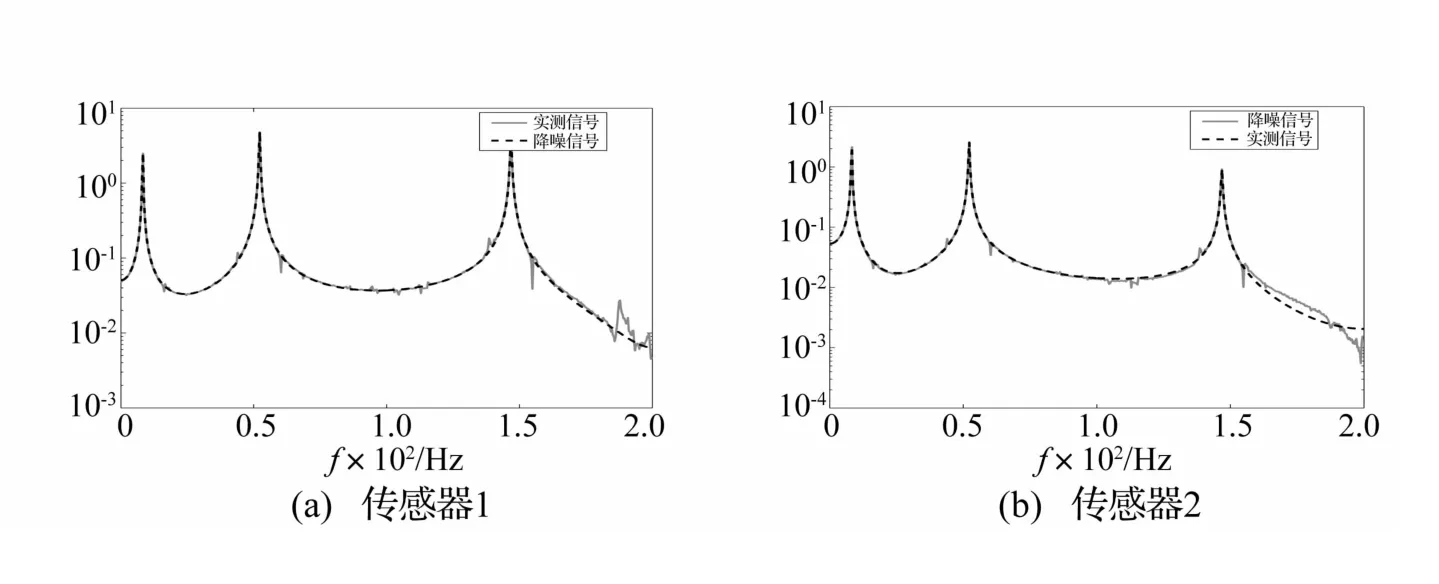
图9 两组信号降噪前后对比Fig.9 Performance of noise elimination for signals related to sensor 1 and sensor 2

表6 用实测信号与降噪信号识别的模态频率 （Hz）Tab.6 The modal frequencies estimated from the measured and filtered signals（Hz）

表7 用实测信号与降噪信号识别的阻尼比Tab.7 The damping ratios estimated from the measured and filtered signals

4 结 论

（1）利用结构的实测脉冲响应信号构造Hankel矩阵，提出利用低秩Hankel矩阵逼近降噪，采用降噪信号进行模态参数识别。经数值算例与模型实验已验证本方法的有效性。

（2）随噪声增强信号中较弱模态易受干扰，模型阶次的确定亦会受影响。

（3）矩阵列数最小时，即使经多次迭代仍无法获得较好降噪效果；矩阵为方阵或接近方阵时，只需较少几次迭代即可获得较好降噪效果。建议使用该方法时用方阵或接近方阵的Hankel矩阵形式。

［1］Ewins D J.Modal testing：theory，practice and applications（2nd edition）［M］.England：Baldock， Hertfordshire，Research Studies Press，2000.

［2］Allemang R J，Brown D L.A unified matrix polynomial approach to modal identification［J］.Journal of Sound and Vibration，1998，211（3）：301－322.

［3］常军，张启伟，孙利民.稳定图方法在随机子空间识别模态参数中的应用［J］.工程力学，2007，24（2）：39－44.CHANG Jun，ZHANG Qiwei，SUN Limin.Application of stabilization diagram for modal paramenter identification using stochastic subspace method［J］.Engineering mechanics，2007，24（2）：39－44.

［4］易伟建，刘翔.动力系统模型阶次的确定［J］.振动与冲击，2008，27（11）：12－16.YI Weijian，LIU Xiang.Order identification of dynamic system model［J］.Journal of Vibration and Shock，2008，27（11）：12－16.

［5］Hu SL J，Bao X X，Li H J.Improved polyreference time domain method for modal identification using local or global noise removal techniques［J］.Sci ChinaPhys Mech Astron，2012，55：1464－1474.

［6］赵学智，叶邦彦，陈统坚.奇异值差分谱理论及其在车床主轴箱故障诊断中的应用［J］.机械工程学报，2010，46（1）：100－108.ZHAO Xuezhi，YE Bangyan，CHEN Tongjian.Difference spectrum theory of singular value and its application to the fault diagnosis of headstock of lathe［J］.2010，46（1）：100－108.

［7］包兴先，刘福顺，李华军，等.复指数方法降噪技术及其试验研究［J］.中国海洋大学学报，2011，41（1／2）：155－160.BAO Xingxian，LIU Fushun，LI Huajun，et al.The complex exponential method based on singalnoise separation for modal analysis［J］.Periodical of ocean university of China，2011，41（1／2）：155－160.

［8］王树青，林裕裕，孟元栋，等.一种基于奇异值分解技术的模型定阶方法［J］.振动与冲击，2012，31（15）：87－91.WANG Shuqing，LIN Yuyu，MENG Yuangdong，et al.Model order determination based on singular value decomposition［J］.Journal of Vibration and Shock，2012，31（15）：87－91.

［9］齐子元，米东，徐章隧，等.奇异谱分析在机械设备故障诊断中的应用［J］.噪声与振动控制，2008，28（1）：82－85.QI Ziyuan，MI Dong，XU Zhangsui，et al.Application of singular spectral analysis in mechanical device fault diagnosis［J］.Nosie and Vibration Control，2008，28（1）：82－85.

［10］段向阳，王永生，苏永生.基于奇异值分解的信号特征提取方法研究［J］.振动与冲击，2009，28（11）：30－33.DUAN Xiangyang，WANG Yongsheng，SU Yongsheng.Feature extraction methods based on singular value decomposition［J］.Journal of Vibration and Shock，2009，28（11）：30－33.

［11］徐锋，刘云飞.基于中值滤波－奇异值分解的胶合板拉伸声发射信号降噪方法研究［J］.振动与冲击，2011，30（12）：135－140.XU Feng，LIU Yunfei.Noise reduction of acoustic emission signals in a plywood based on median filteringsingular value decomposition［J］.Journal of Vibration and Shock，2011，30（12）：135－140.

［12］钱征文，程礼，李应红.利用奇异值分解的信号降噪方法［J］振动、测试与诊断，2011，31（4）：459－463.QIAN Zhengwen， CHENG Li， LI Yinghong. Noise reduction using singular value decomposition［J］.2011，31（4）：459－463.

［13］De Moor B.Total least squares for affinely structured matrices and the noisy realization problem［J］.IEEE Trans Signal Process，1994，42（11）：3104－3113.

［14］Hu SL J，Bao X X，Li H J.Model order determination and noise removal for modal parameter estimation［J］.Mechanical Systems and Signal Processing，2010，24（6）：1605－1620.