基于EEMD自适应形态学在齿轮故障诊断中的应用
侯高雁,吕 勇,肖 涵,秦 拓
(武汉科技大学 机械自动化学院,武汉 430081)
齿轮在旋转过程中必然会产生振动,振动信号包含了齿轮运转过程中的大量信息,在齿轮发生故障时,会产生周期性的脉冲冲击力,引起系统的非线性振动,这使得从齿轮系统获得的振动信号往往具有非线性非平稳特征,因此传统的信号处理方法就无法得到满意的结果。常见的非线性、非平稳信号处理方法有:短时傅里叶变换(STFT);小波变换;Hilbert-Huang变换;EMD等,均具有各自的局限性,为了克服这些不足,提出了基于EEMD自适应形态学方法,来提取故障信号的特征频率。
数学形态学[1]分析是基于积分几何和随机集的不同于时域、频域分析的非线性方法。该方法具有很强的抑制脉冲干扰的能力,并且算法简便易行、实用有效。但是存在选择最优结构元素和滤除白噪声能力不足的问题,针对这一不足,分别采用遗传算法来优化结构元素和EEMD(集合经验模式分解)方法来滤除白噪声。遗传算法[2](GA)是Holland提出的一种随机化的概率搜索方法,能在搜索中自动获取和积累有关知识,实现全局范围内高效、并行的搜索,以求取最优解。Huang等[3]提出一种新的非平稳信号处理方法——经验模式分解(Empirical Mode Decomposition,EMD),该方法核心是将任意信号分解为固有模态函数(IMF),可以进行二次滤波,但该方法会产生模式混叠。为了抑制模式混叠,Wu等[4]提出一种将噪声辅助分析应用于经验模式分解中的集合经验模式分解方法(EEMD),该方法促进抗混分解,有效的抑制了混叠现象。文献[5]将EEMD应用于对大型旋转机械启动过程中振动信号的降噪,结果表明EEMD降噪可以克服EMD降噪方法对脉冲干扰下振动信号滤波能力的不足。
1 遗传形态学
数学形态学是一种针对形状变换的方法。它的基本思想是利用一定形态的结构元素去探测和提取图像或信号中的对应形态,以达到对图像或信号进行分析与识别的目的。
1.1 数学形态学基本运算
腐蚀和膨胀两种算子是数学形态学的基本运算。设采样得到的一维多值信号(待处理信号)f(n)和一维结构元素序列 g(n)的定义域分别为 Df={0,1,2,…,N-1}和 Dg={0,1,2,…,M-1},其中 N和 M都是整数,且N>M。

数学形态学的腐蚀运算抑制正冲击,平滑负冲击;膨胀运算可以平滑正冲击,抑制负冲击;开运算用于滤除信号上方的峰值噪声,去除信号边缘的毛刺;闭运算用于平滑或抑制信号下方的波谷噪声,填补信号的漏洞和裂纹。
1.2 形态学滤波器
利用开运算和闭运算的组合可以构造形态学分析算法,常用的有两种滤波器,AVG和DIF滤波器。
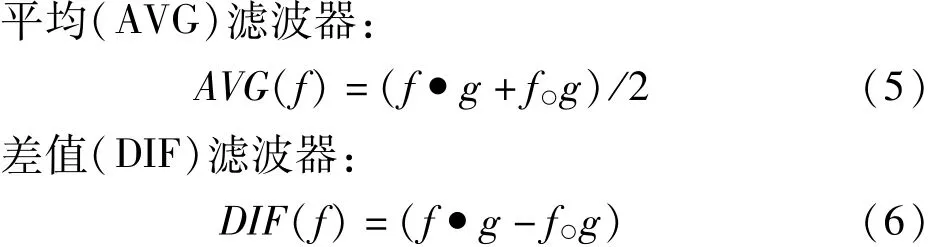
平均滤波器可以同时消除信号中的正、负冲击,对信号起到平滑作用,而差值滤波器,可以提取信号中的正、负冲击。
1.3 遗传算法优化形态学结构元素
遗传算法[2](Genetic Algorithms,GA)是一种新近发展起来的搜索最优解方法,它模拟生命进化机制,即模拟自然选择和遗传进化中发生的繁殖、交配和突变现象,从任意一个初始种群出发,通过随机选择、交叉和变异操作,产生一群新的更适应环境的个体,使群体进化到空间中越来越好的区域。
结构元素是形态学的基本算子,它的选择在于其形状和尺寸(大小)的确定。结构元素的形状一般选择对称的结构,因为非对称时运算会产生偏移,结构元素可以选择为圆盘形、余弦、三角形、正方形、菱形、六边形、线段形等。结构元素越简单,计算量越小,结构元素越接近待提取的特征形状,提取效果越好。考虑到计算量和提取效果[5],选择扁平的圆盘形结构元素。圆盘形结构元素通过半径R来定义它的大小,R越大,闭运算时造成过度粘连,开运算时发生假断裂;R过小,闭运算不能实现裂口较大的断裂边缘连接,开运算时无法去除较大的凸起。为了实现自动化搜索最优R值,采用遗传算法来寻求最优R解,通过信噪比来衡量,信噪比越大,滤波误差越小,则提取效果越好。将R设定在[1,40]范围内,由于R仅能选择整数,从R=1开始执行,一直循环到R=40,按公式7,从中选择出信噪比Y最大的一组,相对应的R值即为最优解。y1为原始信号的平方和,y2为噪音信号的平方和,Y为信噪比。
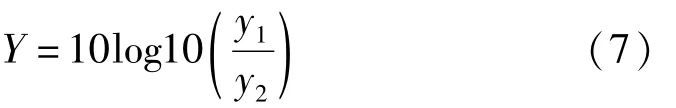
2 EEMD基本原理
EEMD(总体经验模态分解)方法是EMD(经验模态分解)的改进,EMD方法会频繁出现模态混叠现象。有以下两种情况:① 一个单独的IMF信号中含有全异尺度;② 相同尺度出现在不同的IMF中。为了避免混叠现象,提出了EEMD方法。EEMD方法,在采集信号中加入特定白噪声,使得分析时间尺度上能有一个统一的参考框架,能够明确分离各个时间尺度,形成一个有效的、自适应的、动态的二进滤波器组,有利于在EMD中的数据分解。
EEMD分解过程如下:
(1)在原始信号y(t)上加上一组白噪声,得到一个目标信号 ym(t);

(2)对ym(t)进行EMD分解,得到目标信号的各个IMF分量;
(3)给目标信号加入M次不同的白噪声,重复以上两步;
(4)对M次试验的每个IMF计算均值;
(5)取相应IMF的均值作为最终的IMF组。
EMD分解可以参考文献[3],EEMD是一种噪声辅助信号分析方法,利用白噪声频谱均衡分布的特点,用白噪声来均衡信号中的中断区域,从而去除模态混叠。
3 基于EEMD的自适应形态学
EEMD是一种噪声辅助数据分析的方法,巧妙地利用了高斯白噪声具有频率均匀分布的统计特性,把信号分解成特征时间尺度由小到大即频率由高到低的一系列IMF分量,而高频IMF分量通常情况下为噪声,选取低频分量进行重构便可实现降噪,能够很好的滤除噪声,同时添加的白噪声平滑了脉冲干扰等异常事件。EEMD的时域分析可获得一系列单分量的固有模态函数,并能获得各个固有模态函数的幅值和频率等信息,能有效消除模态混叠的影响。
采用EEMD降噪后,用形态学差值滤波器来提取故障信号的特征频率,形态学的结构元素选择圆盘形,采用遗传算法来搜索最优R解,将最优R解代入到差值滤波器中,从而提取出故障信号的特征频率,大大节省了计算和分析时间,能够自适应的选择结构元素的尺寸大小,同时也能够在短时间内寻找到最优解。
4 仿真实验
为了验证所提出方法的有效性,用如下仿真信号进行实验:

其中 x1(t)=cos(2·π·30·t)+1.8cos(2·π·50·t),频率为30和50的谐波信号,如图1所示;x2(t)为标准差为1的高斯白噪声;x3(t)为周期性的指数衰减冲击信号(频率为20Hz,每周期内冲击函数为exp(-20t)sin(20·π·t)),对信号 y(t)进行采样的频率为1 000 Hz,采样时间为2 s,得到的混合信号如图2所示。

图1 谐波信号 x1(t)Fig.1 Harmonic signal x1(t)

图2 仿真信号 y(t)Fig.2 Simulation signal y(t)
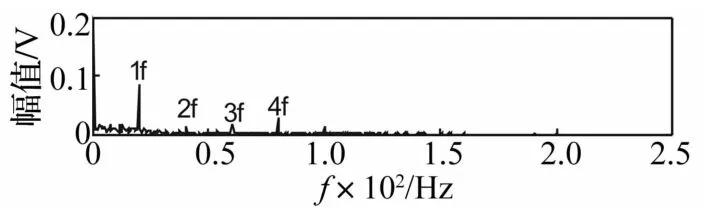
图3 基于EEMD的遗传形态学处理后得到的信号频谱图Fig.3 EEMD based genetic signal spectrum morphology after treatment
此实验的目的是为了抑制谐波信号(30和50 Hz的余弦信号)和白噪声,从而提取信号中的冲击成分(即20 Hz的冲击成分)。
采用提出的方法,先对信号进行EEMD分解,选择有效的信息求和重构,然后用形态学差值滤波器提取冲击成分,结构元素选择圆盘形,利用遗传算法来选择最优R值,最后得到的频谱图如图3所示,不仅抑制了谐波信号和白噪声,而且明显的提取出20 Hz的冲击信号及其2倍频信号、3倍频信号,同时也没有出现模式混叠现象,证明了所提出方法的有效性。
5 自适应形态学和EEMD在齿轮故障诊断中的应用
在齿轮箱故障诊断试验平台上进行试验,齿轮箱为1级降速齿轮传动,输入轴齿轮齿数为20,输出轴齿轮齿数为37,传动比为1.85,齿轮模数为3,输入轴转速为363 r/min。分别模拟齿轮局部断齿和齿轮局部磨损两种故障,人为将齿轮进行断齿和磨损处理,如图4和图8分别为断齿信号和磨损信号的时域图。采样频率为2 000 Hz,采样点数为10 000。
图5为断齿信号经EEMD分解的结果,设定集总平均次数为100,一共分解出了11个经验模态函数(IMF),这里只选择能量较大的前5个IMF进行分析,将前5个IMF分量进行组合,然后用形态学差值滤波器解调,解调后的结果如图6(a)所示。
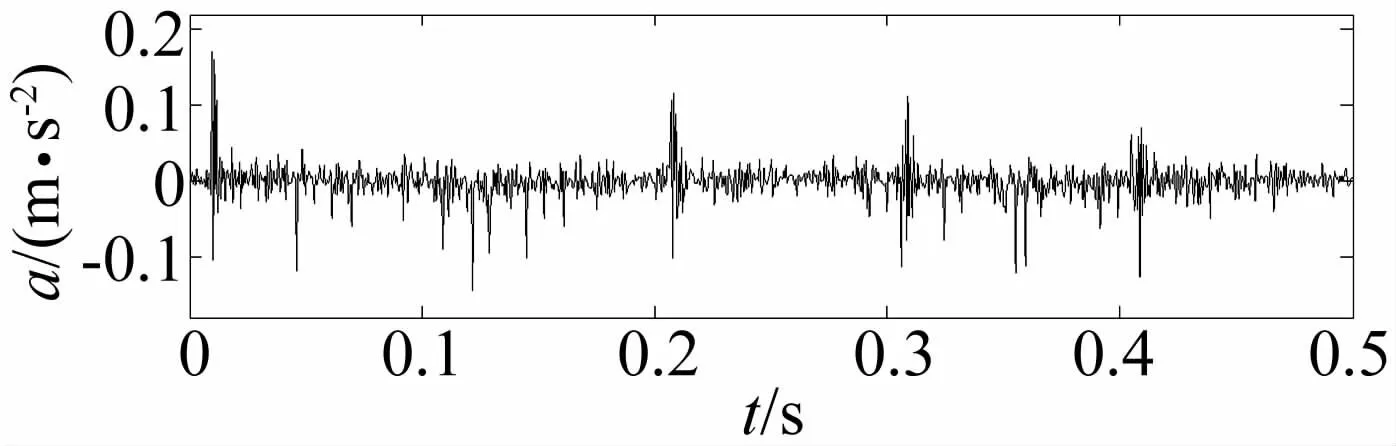
图4 断齿信号时域图Fig.4 Broken teeth signal time domain graph
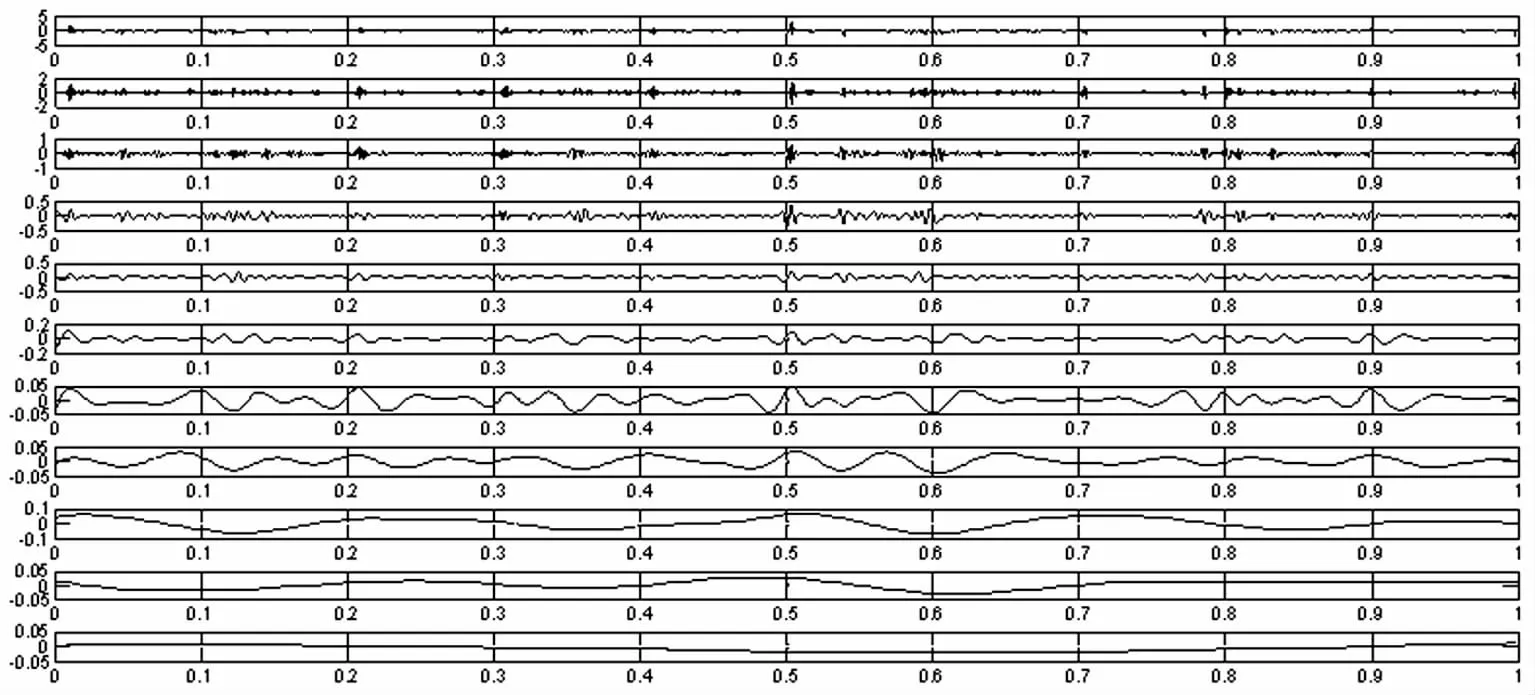
图5 断齿信号经EEMD分解后的结果Fig.5 The result of the broken teeth signal after EEMD decomposition
从图6(a)中明显的看到采用提出的方法,可以清晰地提取出故障频率的1倍频、2倍频、3倍频等倍频信息,以及边频信息。边频信息的数量多、幅值不高、分布均匀,是典型的局部缺陷的标志,而且倍频信息特别明显,幅值高、数量多,故猜测是发生局部断裂,与齿轮模拟故障相吻合。图6(b)和图6(c)分别为用EMD和SVD提取故障频率的结果,图6(a)的提取效果要优于其他两图的效果。图7为磨损齿轮的时域图,图8(a)为经EE-MD自适应形态学解调后的结果,图8(b)和图8(c)分别为经EMD方法和SVD方法提取后的结果。

图6 断齿信号经过处理后的结果Fig.6 Broken teeth signals after treatment

图7 磨损信号时域图Fig.7Wear signal time domain graph
由图8(a)可以看出故障频率的1倍频、2倍频、3倍频信息以及边频信息,边频信息幅值不高、数量多、均匀分布,说明是处于局部缺陷,倍频信息的幅值不高、数量不多,猜想是发生了局部磨损,假设与实际相吻合。比较图8(a)、图8(b)和图8(c),表明提出的方法提取的效果要优于其余两种方法,证明了该方法的有效性。

图8 齿轮磨损信号经过处理后的结果Fig.8Wear signals of the gear after treatment
6 结 论
针对旋转机械振动信号的非线性非平稳性,提出自适应形态学和总体经验模式分解相结合的方法,将该方法应用于齿轮的断齿和磨损故障实验中,结果表明该方法能有效地提高形态学的解调性能。结论如下:
(1)EEMD可以有效抑制经验模式分解EMD处理非线性非平稳信号时产生的模式混叠现象,并且较EMD能够更好的滤除白噪声。
(2)遗传算法可以实现形态学结构元素的优化,快速、准确地寻找出最优解。
(3)该方法能够明显的从故障信号中提取出故障信号的特征频率,且优于EMD和SVD两种方法,为齿轮故障诊断做好准备。
[1]Serra J.Morphological filtering:an overwiew[J].Signal Process,1994,38(1):3-11.
[2]赵春江,施文康,邓勇,等.基于遗传算法优化的多尺度形态边缘检测方法[J].计算机应用与软件,2007,24(4):38-40.ZHAO Chun-jiang,SHIWen-kang,DENG Yong,et al.Multi-scalemorphological edge detection based on genetic algorithm optimizationmethod[J].Computer Applications and Software,2007,(4):38-40.
[3] Huang N E,Shen Z,Long S R,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis[J].Proc.R.Soc.Lond.A,1998,454:903-995.
[4]Wu Z,Huang N E.A study of the characteristics ofwhite noise using the empiricalmode decompositionmethod[J].Proc.R.Soc.1Dndon A,2004,460(2046):1597-1611.
[5]赵昭,刘利林,张承学,等.形态学滤波器结构元素选取原则研究与分析[J].电力系统保护与控制,2009,37(14):21-25.ZHAO Zhao,LIU Li-lin,ZHANG Cheng-xue,et al.Large EEMD noise reduction method for non-stationary vibration signal of rotating machines[J].Power System Protection and Control,2009,37(14):21-25.
[6]曹冲锋,杨世锡,杨将新,等.大型旋转机械非平稳振动信号的 EEMD降噪方法[J].振动与冲击,2009,28(9):33-38.CAO Chong-feng,YANG Shi-xi,YANG Jiang-xin,et al.Large EEMD noise reduction method for non-stationary vibration signal of rotating machines[J].Journal of Vibration and Shock,2009,28(9):33-38.
[7]罗洁思,于德介,彭富强,等.基于EMD的多尺度形态学解调方法及其在机械故障诊断中的应用[J].振动与冲击,2009,28(11):84-86.LUO Jie-si,YU De-jie,PENG Fu-qiang,et al.Multi-scale morphological demodulation method based on EMD and its application in mechanical fault diagnosis[J].Journal of Vibration and Shock,2009,28(11):84-86.
[8]章立军,徐金梧,阳建宏,等.自适应多尺度形态学分析及其在轴承故障诊断中的应用[J].北京科技大学学报,2008,30(4):441-445.ZHANG Li-jun,XU Jin-wu,YANG Jian-hong,et al.Adaptive multi-scale morphological analysis and its application in bearing fault diagnosis[J].Journal of Beijing University of Science and Technology,2008,30(4):441-445.

