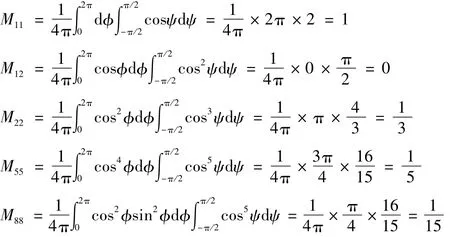单个二阶组合水听器的性能分析
王绪虎,陈建峰,韩 晶,张群飞
(1.青岛理工大学 通信与电子工程学院,山东 青岛 266520;2.西北工业大学 航海学院,西安 710072)
在水下信息的感知和测量系统中,声压水听器是最常使用的传感器,它测量某点的声压,获取声场的标量信息。矢量水听器(AVS:Acoustic Vector Sensor)可以同时测量声场中某点的声压和三个正交的振速分量(或声压梯度),高阶水听器可以获取声场中的高阶差分量,理论上它们获取了更多的声场信息,因而也具有更高的处理增益和空间指向性,近年来受到水声工作者的关注。
矢量水听器的优势在于它具有与频率无关的偶极子指向性,单个矢量水听器便可实现三维空间的无模糊定向[1-2]。近几十年来,矢量水听器技术获得了快速的发展,一批性能稳定的矢量水听器已经成功的应用到声纳浮标[3-4]、声纳潜标[5]、拖曳线列阵[6-7]、辐射噪声测量与识别系统[8-9]地震监测系统[1]、鱼探仪[3]等水下信息感知系统中[10-11]。
声场高阶信息量的幅度相对于零阶信息的(声压)幅度来说比较小,且阶数越高,幅度衰减越快。除此之外,高阶信息量测量系统中具有自噪声,且对环境噪声比较敏感,因而声场高阶信息的获取具有很大的挑战性。近十几年来,一些研究者针对二阶组合传感器进行了相关研究。D’Spain[12]提出了二阶声场的概念,并分析了单点零阶、一阶和二阶信息的波束形成原理;Cray等[13]提出了二阶组合水听器的概念,并分析了单个二阶组合水听器的指向性和处理增益;Cray等[14-15]制作出几种不同类型的二阶组合水听器;Cox等[16-17]针对二阶组合水听器的波束形成、阵列增益和方位估计等内容进行了探索研究。
二阶组合水听器有多种组合方式,本文针对一种十通道的二阶组合水听器进行研究,分析它在各向同性噪声场中输出的自相关特性,在此基础上分析它的的工作性能,从波束指向性和处理增益两个角度上来定量的分析二阶组合水听器的工作性能。为二阶组合水听器的工程应用提供理论支持。
1 二阶组合水听器的测量模型
二阶组合水听器可以同时测量声压、振速和振速梯度(二阶声场信息)信息[13]。图1为三维空间的坐标系,根据平面波声场中声压与质点振速的关系,质点振速的三个正交分量可分别表示为
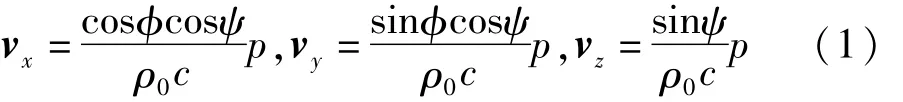
式中,p为声压,c为介质中的声传播速度,ρ0为介质密度,Ф为方位角,ψ为俯仰角。由上式可知,三个振速分量的横向振速梯度可表示为
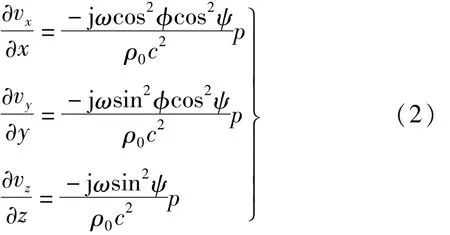
式中,j表示虚数单位,ω为信号的角频率。三振速分量的纵向振速梯度可表示为
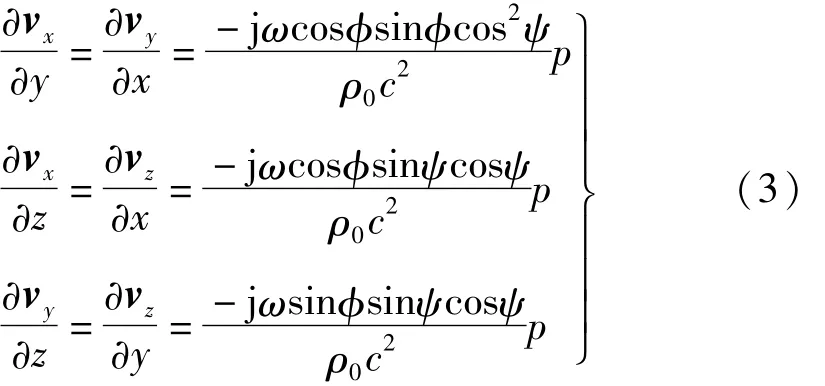
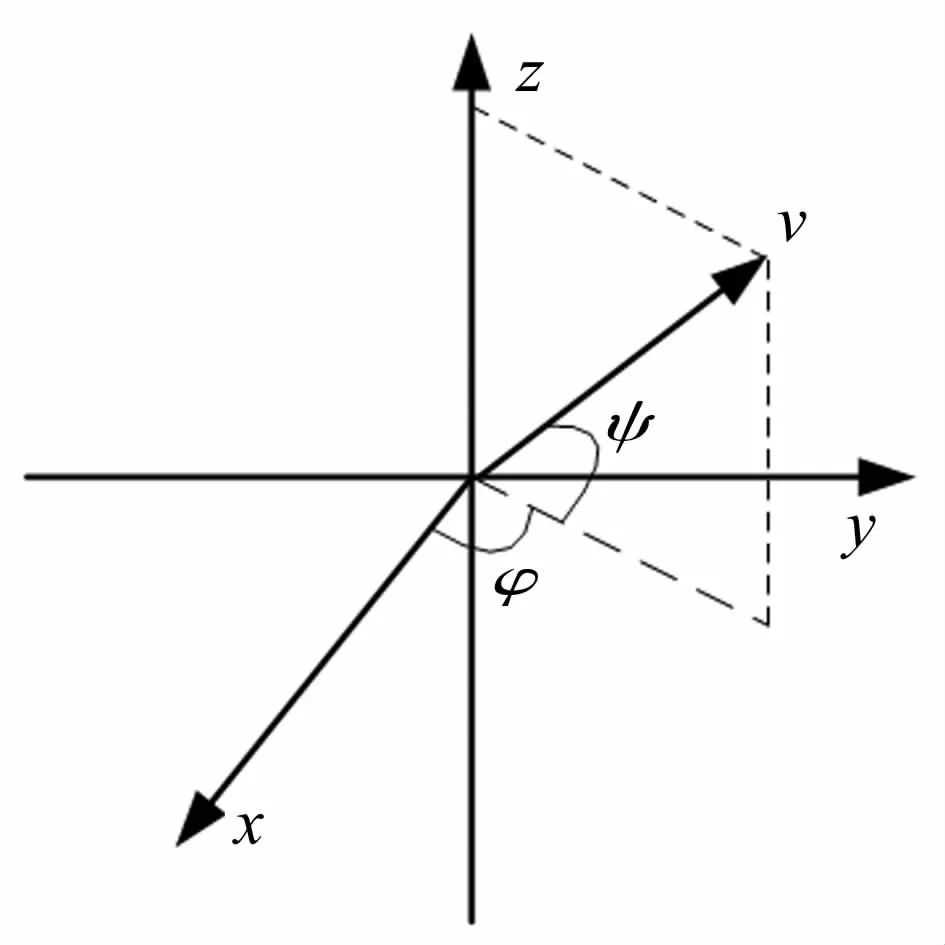
图1 振速在三维空间坐标系中的投影关系Fig.1 Projection relation of vibration velocities in different coordinate system
2 环境噪声场中二阶组合传感器的输出相关性
评估指向性水听器的工作性能,首先要确定水听器输出噪声的自相关特性。为了叙述简单,本文假定环境噪声场为各向同性的。非各向同性噪声可以采用类似的方法进行分析,但计算过程更加复杂。
各向同性噪声场可认为是来自四面八方的平面波噪声共同作用的结果,每个方向来的噪声是互不相关的[18]。因而,二阶组合传感器输出的自相关矩阵R可表示为

式中表示某固定方向上的平面波噪声的自相关系数,且在所有的方向上都相等。U为二阶组合传感器的方向矢量,具体形式为
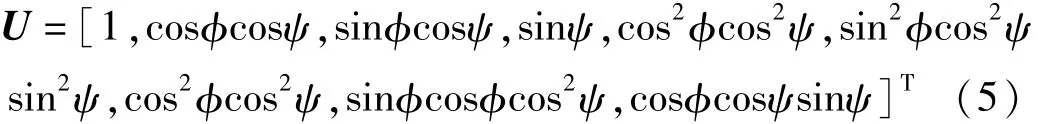
M表示归一化的自相关矩阵,其值为
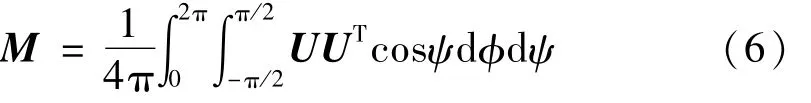
将式(5)代入式(6)可得(为了保持叙述的连贯性,这里直接给出结果,附录中进行了详细分析)

3 二阶组合传感器的波束形成
波束形成是阵列信号处理常用的一种方法,它将基阵各阵元输出经过处理(如加权、延时、求和等)形成空间指向性。其目的之一是滤除噪声,提高系统输出的信噪比。二阶组合传感器有10个输出通道,可以类比于10阵元基阵进行波束形成处理,来滤除噪声,提高其输出信噪比。
3.1 常规波束形成
二阶组合水听器的输出用矩阵形式表描述,可以写成

式中,X(t)为二阶组合水听器的输出信号矢量,x(t)为二阶组合水听器等效中心点处的声压信号波形,U(Ω)为其方向矢量(具体形式如式(5)所示),Ω=(Ф,ψ)表示信号的方位矢量,N(t)为组合水听器的噪声信号矢量。
利用方向矢量对二阶组合水听器的接收信号进行匹配处理,其处理过程如图2所示,则其输出功率可表示为
式中,W=U为波束形成的权向量,N为快拍数。为二阶组合水听器接收信号的自协方差矩阵,具体形式为
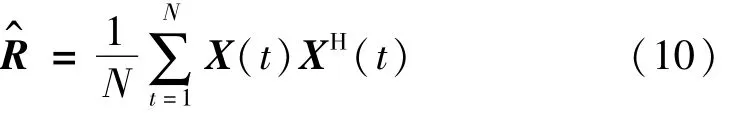
式(9)表示的处理过程成为二阶组合水听器的常规波束形成(CBF:Conventional Beamforming)。
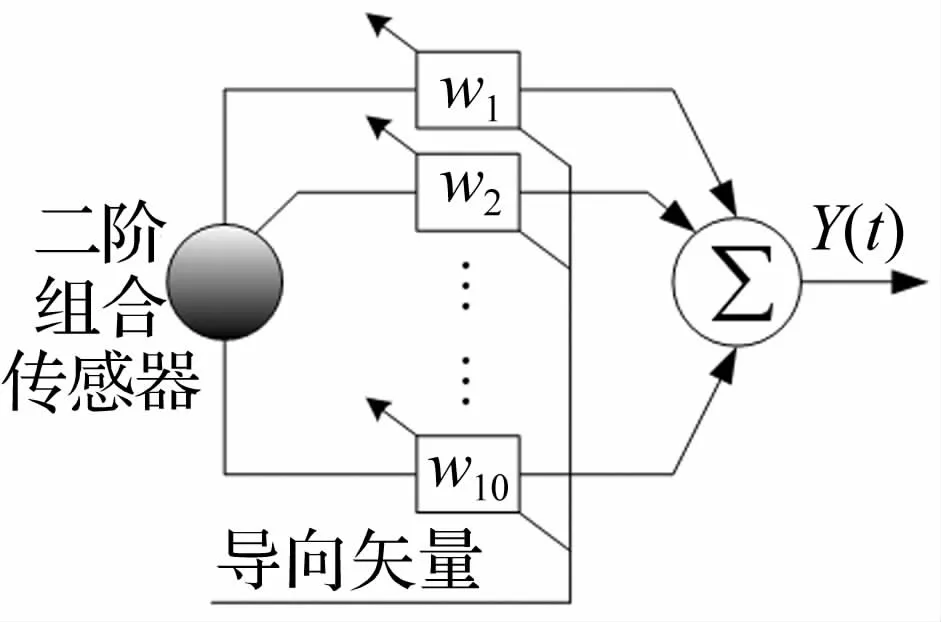
图2 二阶组合水听器常规波束形成原理图Fig.2 Function diagram of the CBF based on single ADS
3.2 MVDR波束形成
对二阶组合水听器的输出进行加权处理,使其满足两个准则:无失真准则和最小方差准则,这样的处理过程称为二阶组合水听器的最小方差无失真响应波束形成(MVDR:Minimum Variance Distortionless Response beam forming)。
无失真准则即要权矢量W在入射波方向上的响应系数满足

式中为入射波的方位,其中 Фs表示方位角,ψs表示俯仰角。最小方差准则即使波束形成器的输出功率P最小。上述问题利用最优化理论可以描述为

利用拉格朗日乘子法可以得出最佳权向量
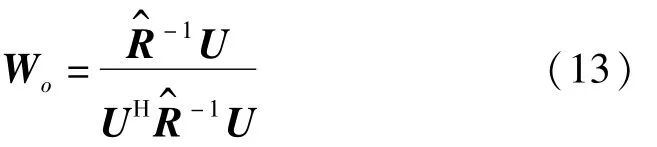
将式(13)代入式(12)可得二阶组合水听器的输出方位谱为
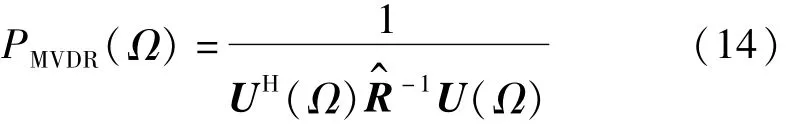
式中U(Ω)为二阶组合水听器的方向矢量为它的数据协方差矩阵。通过式(14)计算出方位谱,对方位谱进行极值搜索便可求得目标的方位。二阶组合水听器的MVDR波束形成处理过程如图3所示。
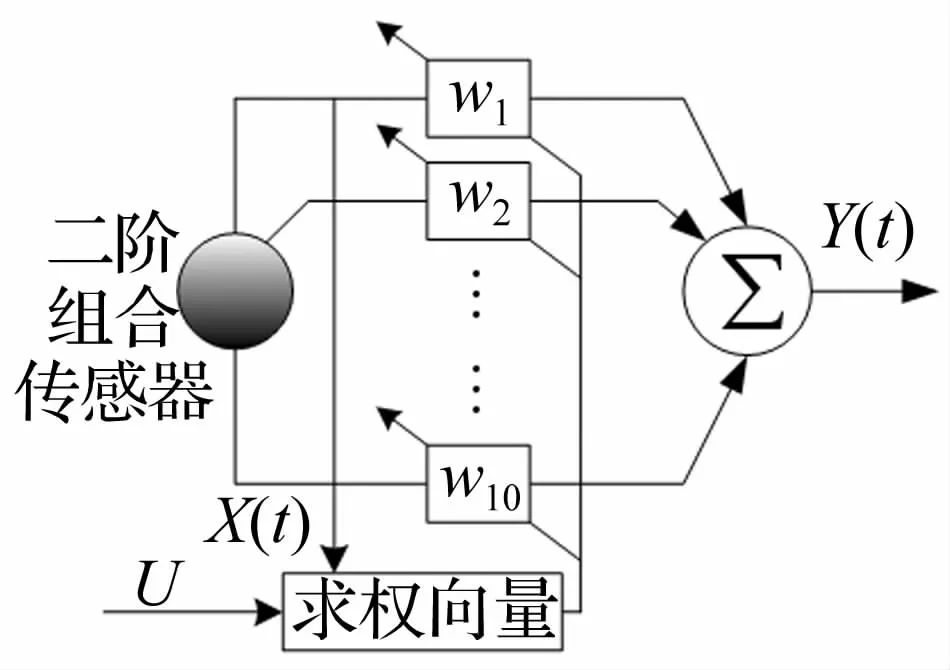
图3 MVDR波束形成原理图Fig.3 Function diagram of the MVDR based on single ADS
注意,式(14)所表示的空间谱跟信号的输出功率没有直接关系;式(9)描述的是系统的输出功率,两者的物理涵义有本质的区别。
3.3 增益分析
处理增益是衡量系统性能的一个重要参数,它定义为系统输出信噪比与系统输入信噪比的比值。下面通过分析二阶组合水听器的两种处理方法的增益来分析其性能。
假定在二阶组合水听器接收端信噪比为SNRin=Ps/Pn,其中Ps表示信号功率,Pn为噪声功率。常规波束形成器的输出端信噪比为
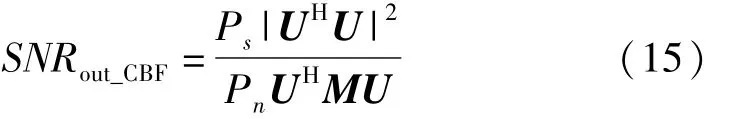
式中,M为二阶组合水听器噪声的归一化协方差矩阵。根据处理增益的定义,二阶组合水听器常规波束形成的处理增益为
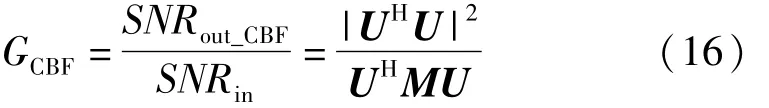
由上式可以看出,二阶组合水听器的常规波束形成器的处理增益由二阶组合水听器的输出噪声相关特性和方向矢量共同决定。
由于二阶组合水听器MVDR波束形成器满足无失真准则,因而其输出的信号功率为Ps;其输出的噪声功率部分可以表示为
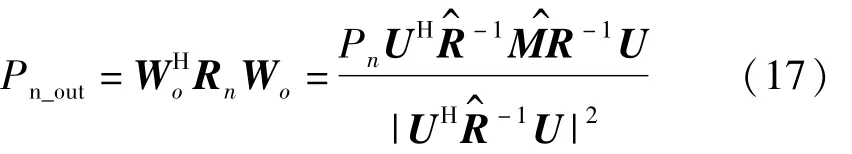
所以,其处理增益为
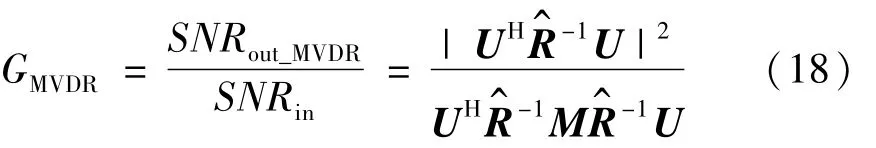
从上式可以看出,二阶组合水听器MVDR波束形成器的处理增益与输入信号有关为二阶组合水听器接收信号的协方差矩阵估计值)。
从上的分析过程可以看出,波束形成的权值W不同,会有不同的处理增益。
4 仿真及结果分析
为了评估二阶组合水听器的性能,对它的两种波束器进行了仿真分析,为了比较,同时给出了单个矢量水听器的仿真结果。
仿真条件:信号频率为1 kHz,采样频率为25 kHz,快拍数取1 024点,噪声为数值模拟的各向同性噪声噪声。
图4为信噪比为10 dB时,二阶组合水听器波束形成的三维波束等高线图。图4(a)是二阶组合水听器MVDR波束图;图4(b)是矢量水听器的MVDR波束图;图4(c)是二阶组合水听器的CBF波束图;图4(d)是矢量水听器的CBF波束图。通过观察和对比我们可以看出:相比于矢量水听器,二阶组合水听器的波束图具有更好的性能,它的波束宽度更窄,旁瓣级更低。这说明二阶组合水听器在较小的孔径下可以获得更好的指向性。

图4 三维波束等高线线图Fig.4 The contourmap of three-dimensional beampattern
图5为信噪比为10 dB,俯仰角ψ=0°时,目标方位角分别为Ф=180°和Ф=135°两种情况的二维波束图。图中实线为二阶组合水听器的波束图,点实线为矢量水听器的波束图。图5(a)和(b)为目标Ф=180°时的CBF和MVDR波束图。图5(c)和(d)为目标Ф=135°时的CBF和MVDR波束图。从图中可以看出,二阶组合水听器的波束性能优于矢量水听器输出波束,且它在180°方向的优势大于在135°方向上的优势。

图5 ψ=0°时二维波束图Fig.5 Two-dimensional beampattern whenψ=0°
文献[3]中分析了矢量水听器常规波束形成处理增益为4.8 dB,且它在各个方向上都是相等的。图6给出了二阶组合水听器常规波束形成的处理增益图,从图上可以看出,二阶组合水听器的常规处理增益在各个方向上是不同的,其最高增益约为6.12 dB,最小增益约为5.23 dB。由此我们可以看出,二阶组合水听器获得了比矢量水听器更大的处理增益。

图6 二阶组合水听器常规波束形成的处理增益Fig.6 The processing gain of the CBF based on single ADS
在方向 Ωs=(180°,0°)上,二阶组合水听器的常规增益为最大值6.12 dB,高于矢量水听器处理增益1.32 dB;在方向 Ωs=(135°,0°)上二阶组合水听器的常规处理增益约为5.46 dB,高于矢量水听器约为0.66 dB。这一点解释了二阶组合水听器波束相对于矢量水听器波束在180°方向的优势大于在135°方向上的优势的内在原因。
图7为二阶组合水听器MVDR波束形成器的处理增益分布图。从图中可以看出,在不同方向上,其增益值是相同的,处理增益值约为在9.54 dB(注意,计算增益时用到噪声协方差矩阵的求递,即对式(7)所示的矩阵求逆,该矩阵条件数差,不能直接求逆矩阵,可以通过求广义等矩阵的方法计算)。对比图6和图7可以看出,在权值与信号方向准确匹配的情况下,MVDR波束形成器的处理增益高于CBF约4 dB左右。

图7 二阶组合水听器MVDR波束形成的处理增益Fig.7 The processing gain of the MVOR beamforming based on single ADS
5 结 论
本文推导了各向同性噪声场中二阶组合水听器的输出协方差矩阵。分析了两种基于单个二阶水听器的波束形成方法,常规波束形成和最小方差无失真响应波束形成,并推导了两种处理方法的增益公式。仿真结果表明,单个二阶组合水听器可以获得更好的指向性和更大的处理增益。其常规波束形成器的处理增益在不同的方向上不同,分布在5.23-6.12 dB之间;二阶组合水听器MVDR波束形成器的增益在各个方向上是相同的,增益值约为9.54。在工程中,二阶组合水听器的MVDR波束形成依然具有阵列信号处理中所具有的稳健性差的缺点。
[1]Nehorai A,Paldi E.Acoustic vector-sensor array processing[J].IEEE Transactions on Signal Processing,1994,42(9):2481-2491.
[2]Hawkes M,Nehorai A.Acoustic vector-sensor beamforming and capon direction estimation[J].IEEE Transactions on Signal Processing,1998,46(9):2291-2304.
[3]杨德森,洪连进.矢量水听器原理及应用引论[M].北京:科学出版社,2009.
[4]贾志富.全面感知水声信息的新传感器技术-矢量水听器及其应用[J].物理,2009,38(3):157-168.JIA Zhi-fu. Novel sensor technology for comprehensive underwater acoustic information—vector hydrophones and their applications[J].Physics,2009,38(3):157-168.
[5]陈晓昭,陈建峰,王绪虎,等.矢量水听器的工程局限性剖析[J].声学技术,2012,31(5):490-496.CHEN Xiao-zhao,CHEN Jian-feng,WANG Xu-hu,et al.Limitations of acoustic vector in engineering application[J].Technical Acoustics,2012,31(5):490-496.
[6]D’Spain G L,Luby JC,Wilson GR etal.Vector sensors and vector sensor line arrays:Comments on optimal array gain and detection[J].J.Acoust.Soc.Am.,2006,120(1):171-185.
[7]Rouquette R E et al.Towed streamer deghosting[P].USA:7167413B1,2007.
[8]孙贵青,杨德森,张揽月.基于矢量水听器的水下目标低频辐射噪声测量方法研究[J].声学学报,2002,27(5):429-434.SUN Gui-qing,YANG De-sen,ZHANG Lan-yue.Research on themethod formeasuring radiated nosie by an underwater target in low ferquency band based on the vector hydrophone[J].Acta Acustica,2002,27(5):429-434.
[9]胡博,杨德森.基于矢量阵测量的局部近场全息技术研究[J].振动与冲击,2011,30(8):225-229.HU Bo, YANG De-sen. Patch near-field acoustical holography study based onmeasurement of vector hydrophone array[J].Journal of Vibration and Shock,2011,30(8):225-229.
[10]孟洪,葛辉良,李冰茹.舷侧阵壳体平台近场声矢量场分析[J].声学技术,2009,28(6):4-7.MENG Hong,GE Hui-liang,LIBing-ru.Analysis of the near vector-field of cylindrical shell’s sound radiation of flank array[J].Technical Acoustics,2009,28(6):4-7.
[11]杨德森,朱中锐,时胜国.球形壳体障板声散射近场矢量特性[J].振动与冲击,2013,32(2):135-139.YANG De-sen,ZHU Zhong-rui,SHI Sheng-guo.Acoustic vector characteristics of near fields scattered by a spherical shell baffle[J].Journal of Vibration and Shock,2013,32(2):135-139.
[12]D’Spain G L,HodykissW S.Array processing with acoustic measurements at a single point in the ocean[J].J.Acoust.Soc.Am.,1992,91(4):2364.
[13] Cray B A,Evora V M,Nuttall A H.Highly directional acoustic receiver[J].J.Acoust.Soc.Am.,2003,113(3):1526-1532.
[14]Cray B A,Evora V.F.Highly directive underwater acoustic receive[P].USA:6697302B1,2004.
[15]杨德森,孙心毅,洪连进,等.基于矢量水听器的振速梯度水听器[J].哈尔滨工程大学学报,2013,34(1):7-14.YANG De-shen,SUN Xin-yi,HONG Lian-jin,et al.The velocity gradient sensor based on the vector sensor[J].Journal of Harbin Engineering University,2013,34(1):7-14.
[16]Cox H,Lai,H.Performance of line arrays of vector and higher order sensors[C]//Proceeding of the 41th Asilomar Conference on Signals, Systems and Computers. Pacific Grove,CA,USA,2007,1231-1236.
[17]LaiH,Bell K.Cramer-Rao Lower Bound for DOA Estimation Using Vector and Higher-Order Sensor Arrays[C]//Proceeding of the 41th Asilomar Conference on Signals,Systems and Computers.Pacific Grove,CA,USA,2007,1262-1266.
[18]Hawkes M,Nehorai A.Acoustic vector-sensor correlations in ambient noise[J].IEEE Journal of Oceanic Engineering,2001,26(3):337-347.
附 录
求解式(6)所示矩阵M的各元素的过程中主要应用了下述的个等式
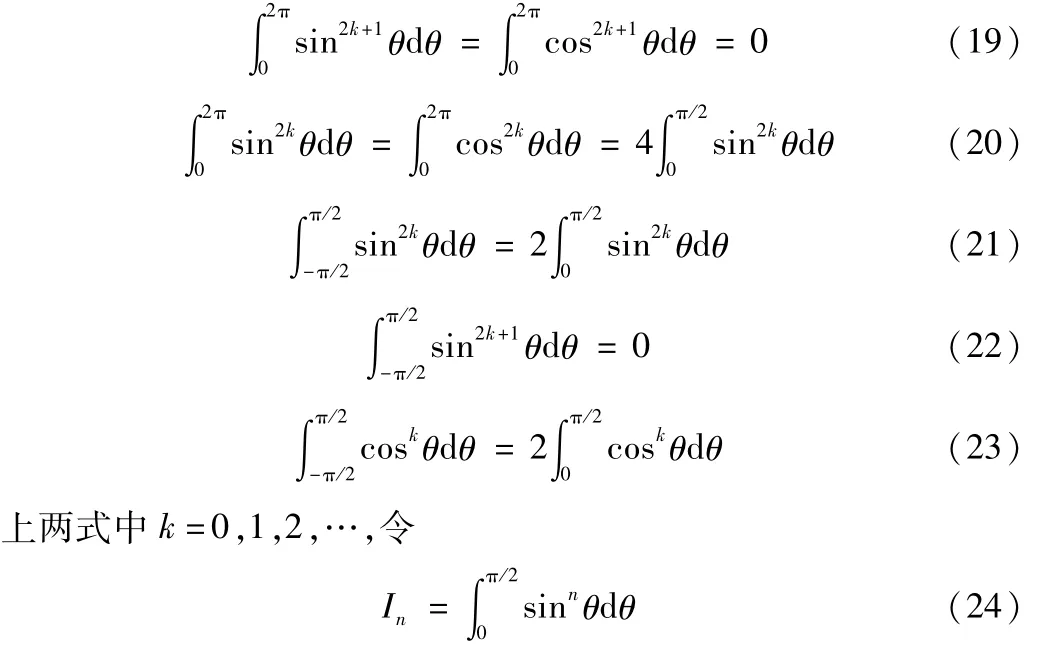
式中n=0,1,2,…,则In可以根据下述的递推关系求解。

下面列出了求解矩阵M的五个元素的过程,做类比推导可以求解出其他的元素。