二自由度行波型超声波电机的轨迹控制
傅 平,胡锡幸,郭吉丰
(1,福州大学 电气工程学院,福州 350108;2,闽江学院 物理学与电子信息工程系,福州 350121;3,国网浙江省电力公司杭州供电公司,杭州 310009;4,浙江大学 电气工程学院,杭州 310027)
二自由度球形超声波电机低速大力矩、定位精度高的特性非常适合做多自由度机器人的执行机构。但是二自由度超声波电机[1-9]具有非线性、时变、强耦合的特性,使得它的转速、位置检测比较困难。目前,国内外关于二自由度球形超声波电机性能测试的报道较少。
二自由度球形超声波电机的输出变量主要是转速、位置。目前在二自由度球形超声波电机中最常用的位置检测机构[4]如图1所示,在电机的x轴和y轴方向上分别安装光电编码器,在每个编码器的轴上安装一个圆弧带槽框架,球转子输出轴通过两条圆弧带槽框架的相交点。通过两个编码器所测得的转角就能得到输出轴的空间位置。这种检测方式需要在球转子上安装一个输出轴,转子的运动范围会受到限制。文献[10]给出了转速和电压的关系图。文献[11]给出了电机绕各轴的最高转速,但其输出转矩因太小而难以检测。文献[12]给出了多自由度球形超声波电机的空载转速和最大输出转矩。文献[13]使用调心轴承和连杆机构来检测球转子姿态角,其运动范围仍受制约。除此之外则是采用视觉识别测量系统,在球转子表面喷涂网格图,并从中提取特征点以识别网格的位置。Lee等[13]使用双光学传感器在2个方向检测球转子的表面变化量,进而测量出球体三自由度的运动姿态。采用光学传感器有助于提高检测精度,但是增加了控制系统的运算量。Mashimo等[14]提出用激光检测球转子的位置,激光的应用进一步提高了检测精度,但也使得成本提高以及检测范围受限。
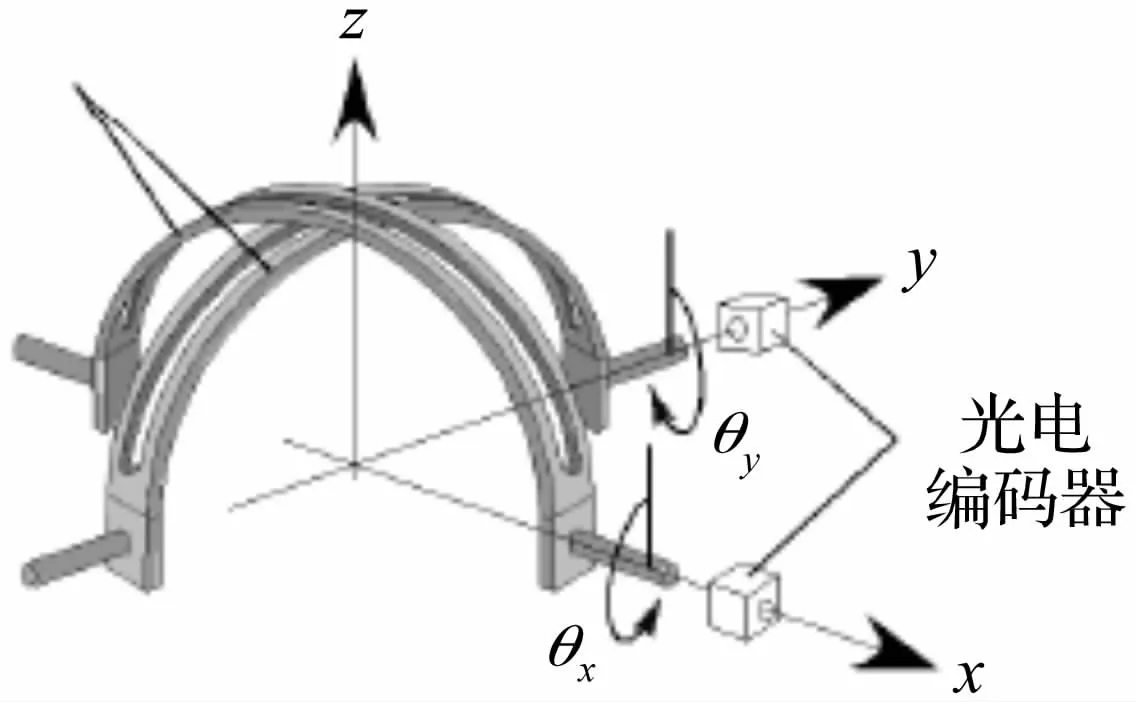
图1 常用的位置检测机构Fig.1 Position detectingmechanism in common use
二自由度球形超声波电机[15]是通过3个定子的相互协调控制来实现球转子的运行,因此研究球转子在单个定子不同频率、相位、幅值以及驱动方式(驻波、行波)下的运行特性是分析二自由度球形超声波电机的基础。实验中,首先进行单定子驱动球转子特性的测试。测试系统采用光电编码器测定球转子转速,转矩测试模块测量球转子的输出力矩,并通过压紧螺母调整加载预紧力的大小。最后再进行二自由度球形超声波电机的轨迹控制。
1 单定子电机的输出特性
电机转速和驱动频率的对应关系如图2(a)所示。从图中可以知道,电机的稳定工作区一般选取在谐振点右侧一段较小的区间,该区间带宽大约为400 Hz,即49.1-49.5 kHz。在工作区间内对应的机械特性如图2(b)所示,可以看到随着驱动频率的增加,电机空载转速和堵转力矩都有所下降。
图3是电机转速随相位差的变化曲线。从图3可以看到,定子两相输入电压的相位差在过零点附近存在一个转速死区。当驱动频率为49.2 kHz时,死区约为 ±20°。
图4是电机转速随输入电压变化曲线。图中可以看到输入电压与转速之间存在一个死区,只有当输入电压的峰峰值超过30 V后,转子才开始运转。
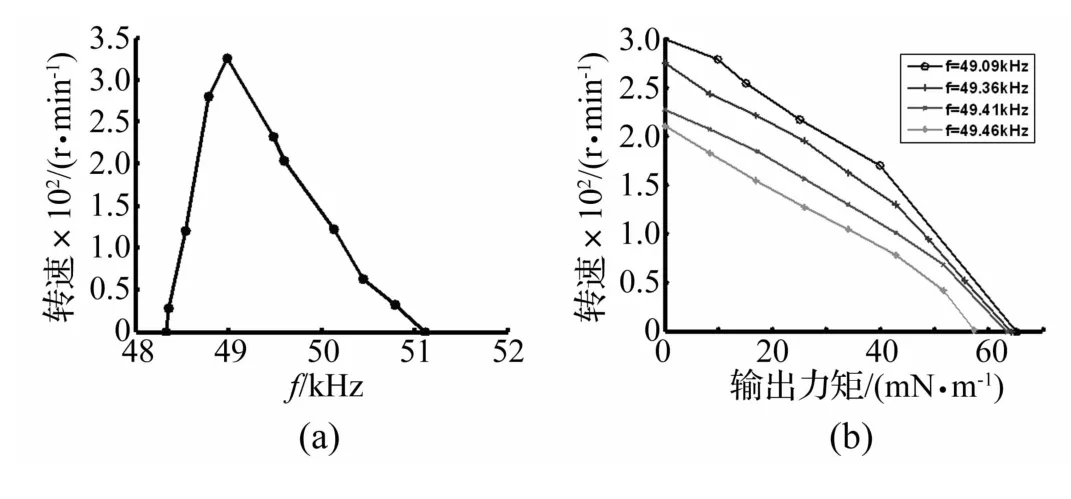
图2 频率-速度特性Fig.2 Speed-driving frequency characteristics
2 轨迹运行控制
对于2自由度超声波球电机而言,平面任意方向的角速度ω都可以通过两个相互垂直的角速度ω1、ω2合成,如图5所示。
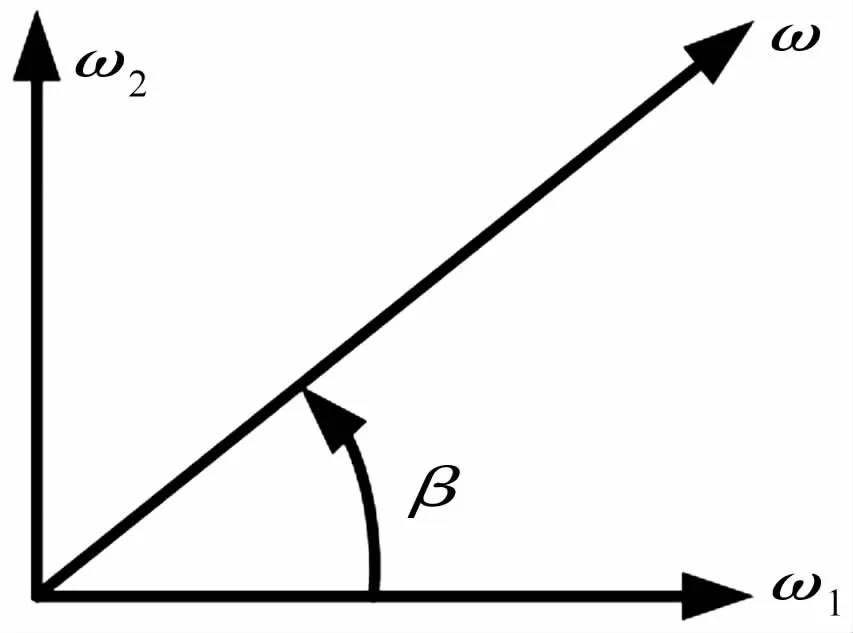
图5 角速度分解Fig.5 Decomposition of angular velocity

图3 转速-相位差特性Fig.3 Speed-driving phase-difference characteristics
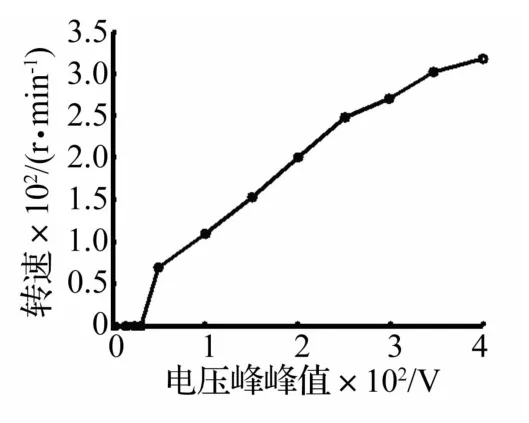
图4 转速-输入电压特性Fig.4 Speed-input voltage characteristics
图5中β表示ω1与ω之间的夹角,它们的关系为
2自由度球形超声波电机包含3个定子,空间呈120°对称分布[15]。假设3个定子表面行波波峰点沿定子周向的角速度分别为 ωs1,ωs2,ωs3,可以得到 ωs1,ωs2,ωs3与 ω1和 ω2之间满足
上式中nx和ny分别为x和y轴的单位向量。
由式(1)、(2)和(3),并以极小范数解作为优化目标,冗余性及其控制策略具体见文献[15]。当控制球转子的空载转速在单位圆内时,可以得到ωs1、ωs2、ωs3满足以下关系
其中k是常数,满足
式(5)中 φ=arccos(r/R),r是定子有效半径,R是球转子半径。
因此,通过配置3个定子表面的角速度就能完成转子在x,y坐标轴内沿任意角度运行。
2.1 转速控制方法
通过合理配置定子表面的角速度就能完成转子在x,y坐标轴内沿任意角度运行。而定子表面的角速度可以通过改变定子输入电压的频率、幅值和相位差进行调整。由单定子电机的输出特性可以知道主要有以下几种方法实现:
(1)调频控制
调频控制是最常用的控制方式,但是2自由度球形超声波电机通过调谐实现三个定子的谐振频率一致。通过调频调速,电机输入频率一旦远离谐振区,就会产生较大的转速波动,影响电机的控制效果。因此不适合采用调频的方式进行控制。
(2)调压控制
调压控制可以实现定子振幅的平稳变化。对于超声波电机而言,调压控制可调节的范围较小。
(3)相位差控制
采用相位差控制可以实现电机转速大小和方向的平稳调整。对于电机而言,相位差控制在降低电机转速的同时,不会带来负载转速的增加。因此运行过程中,通过改变相位差对电机进行转速调整,可以在调速时保证电机平稳运行。为了确定单个定子驱动时电机转子转速和定子两相相位差之间的对应关系,需要对图3的数据进行拟合。由图3可以看出电机转速和相位差之间呈现较强的非线性关系,大大增加了实际控制过程的运算量。通过分段线性拟合,可以得到电机转速n与定子两相相位差θ之间的对应关系

单定子驱动时相位差θ与转速n对应关系的实测点与式(6)拟合曲线的对比如图6所示,从图中可以看到拟合曲线和实际测试点基本接近,能够反映电机转速随相位差的变化规律。
联立式(4)和(6),并采用归一化处理,可以得到β与定子1相位差θ1之间满足
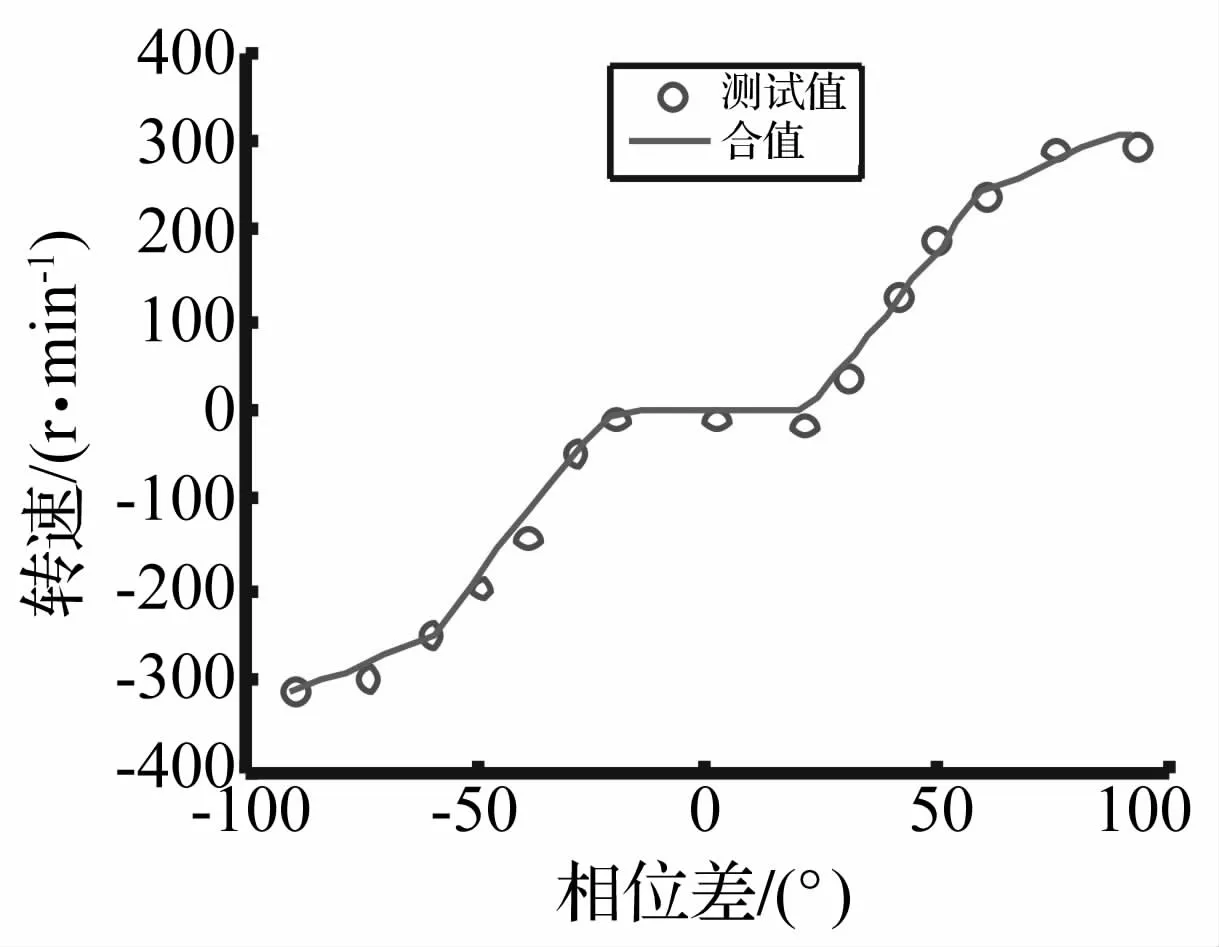
图6 定子相位差与转速对应关系Fig.6 Relation between speed of rotor and phase difference of each stator

其中nmax=300 r/min。同理 θ2和 θ3也可以通过同样的方法得到。通过式(7)以及定子相位差的对应关系,可以得到β与各个定子的对应关系如图7所示。由图7可以看到,定子相位差θ与β角的对应关系并不连续,这是由于调相时电机存在运行死区。
2.2 驱动控制系统
2自由度超声波电机驱动控制系统由PWM控制电路、驱动电路、位置检测和信号处理电路这四部分构成。其中PWM控制电路主要完成反馈信号的采集,以及PWM波形的输出。驱动电路通过光耦和推挽电路将PWM信号放大并驱动电机运转。位置检测把球转子的旋转角度通过光栅转化为正弦信号输出。信号处理电路将光电编码器输出的信号滤波、放大、整形,使电机的位置输出信号能被控制电路采集。
(1)PWM控制电路
PWM控制电路采用TI公司的TMS320F28335作为PWM发生和反馈信号采集的控制芯片。
(2)驱动电路
驱动电路将PWM信号放大,输入到推挽电路中,再对电机进行阻抗匹配,关于驱动电路,可参考文献[13],这里就不再作相应介绍。
(3)位置检测
电机的位置检测包括电机本体、栅轮、胶质滚球等组成,如图8所示。位置检测机构上的码盘齿数n=45,码盘细杆直径d=2 mm,球转子直径D=40 mm。因此位置检测机构x、y两个方向上的精度δ可以达到
光电信号输出电路输出四路方波,通过测量方波信号及其顺序就可以得到电机转子的相应位置。
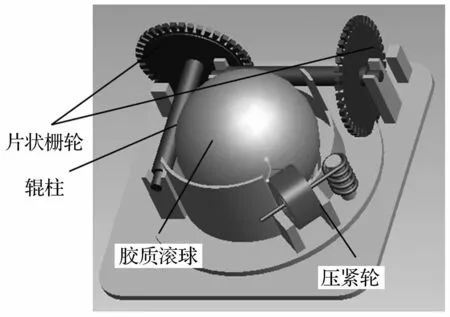
图8 检测机构示意图Fig.8 Diagram of detection mechanism
(4)信号处理电路
光电编码器输出方波信号,幅值只有1 V左右,而且还伴随着大量的谐波干扰。为此需要对信号进行放大、滤波和整形。电路如图9所示。
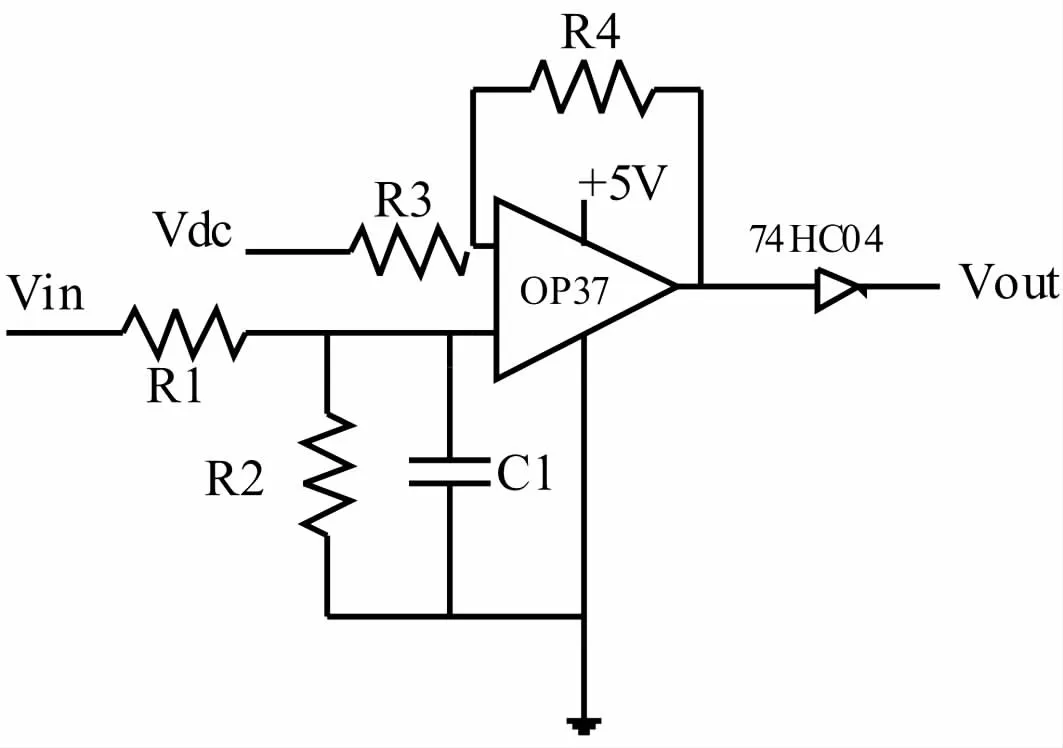
图9 信号处理电路Fig.9 Circuit of signal processing
若只采用相位差控制,当β为60°时,3个定子两相的相位差分别为45°、45°和 -90°。图 10(a)是 x轴和y轴编码器的运行转速。从图10(a)可以看到,编码器运行较为平稳,其中x轴编码器的转速波动在8.5%以内,而y轴的转速波动在5%以内。通过x轴和y轴编码器的转速可以得到β的实际值。图10(b)是β的设定值和实际值,可以看到β设定值和实际值之间最大相差 8°。
表1是设定β后对应的3个定子的角速度ωs1、ωs2、ωs3的比例关系和每个定子的相位差。图11是设定β和3个定子两相的相位差后电机的开环运动轨迹。
实验时,球转子的运动姿态用转子表面某点的运动轨迹描述,为简单起见,具体的运动位置直接采用光电编码器的脉冲数表示,如设定沿直线运动,直线的边界位置分别为(60,100),(-60,100),(-60,-100)和(60,-100),实际运动轨迹如图11所示,图中虚线表示设定轨迹,实线为电机实际运行轨迹。由图11可以得到,不同β下实际运行轨迹与设定值之间存在一定误差,其中β为60°时,误差较大,达到8°;β为180°时,误差较小,只有4°。
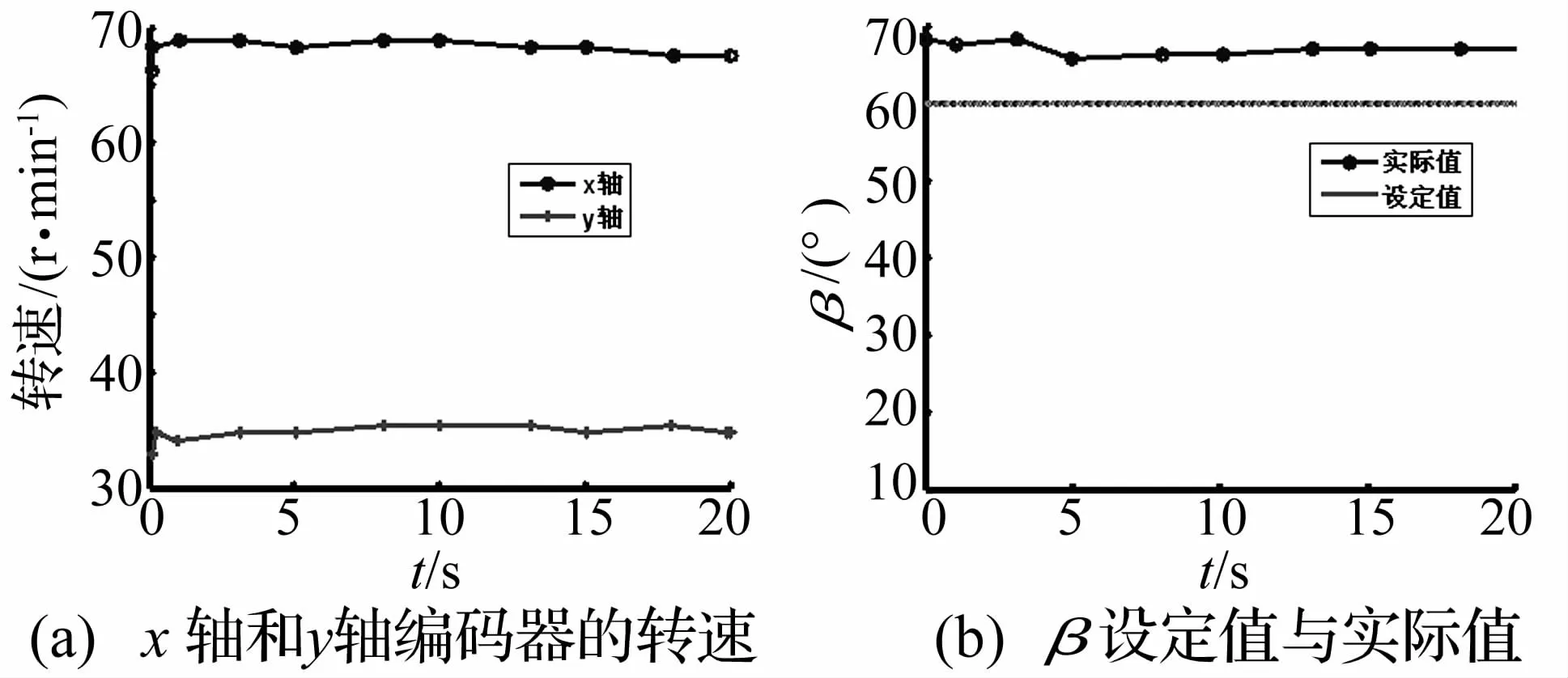
图10 转速与β情况Fig.10 Speed and changing ofβ

表1 不同β下定子1、2、3的相位差Tab.1 Phase-difference of stator 1、2、3 with differentβ
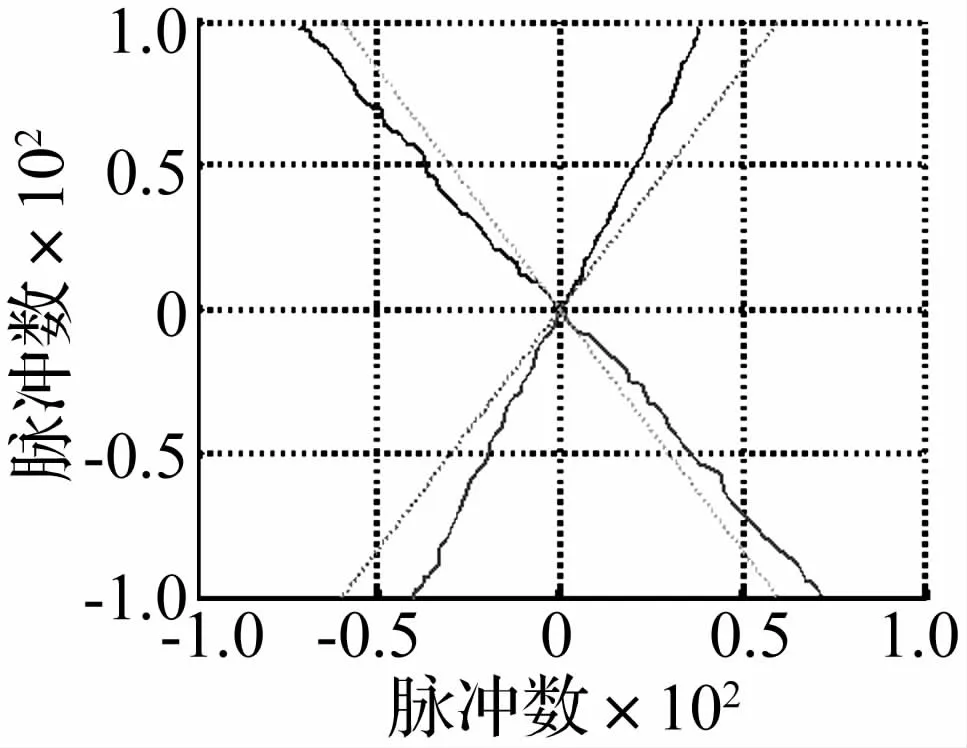
图11 电机开环运动轨迹Fig.11 Trajectory ofmotion by open loop control
2.3 闭环控制方法
从前面的结果可以知道,开环控制中β误差较大。对于轨迹控制而言,需要对电机进行闭环控制,才能实现良好的轨迹跟踪。

图12 轨迹闭环控制原理图Fig.12 Diagram of trajectory by closeloop control
如图12所示,假设电机转子上某点初始位置为O,目标位置设为P,通过前面的结果可以知道,使用开环控制达不到理想的控制效果,为此采用分段逐点比较法来实现电机的轨迹控制。
假设在初始位置,O点与电机圆心重合,运行到目标位置P所对应的运动矢量与x轴的夹角为β。通过式(7)可确定3个定子的两相相位差。由于开环控制的误差,当电机运行到P1点,其中圆心到P1点与x轴的夹角为 α1,则

当e(k)≤0,需要减少转子运动矢量与x轴之间的夹角,并通过式(7)确定各定子的两相相位差。当e(k)>0时,需要增加转子运动矢量与x轴之间的夹角,并通过式(7)确定各定子的两相相位差。当目标位置P坐标与电机实际运动位置Pi坐标符合(ε为设定阈值)时认为电机到达指定位置,完成闭环轨迹控制。
由于超声波电机运行时存在一定的非线性,传统的PID控制效果较差,我们采用了文献[16]的神经元PID算法对电机进行控制。神经元学习控制所需要的状态量为 x1(k)、x2(k)、x3(k)。这里,x1(k)、x2(k)、x3(k)分别定义为
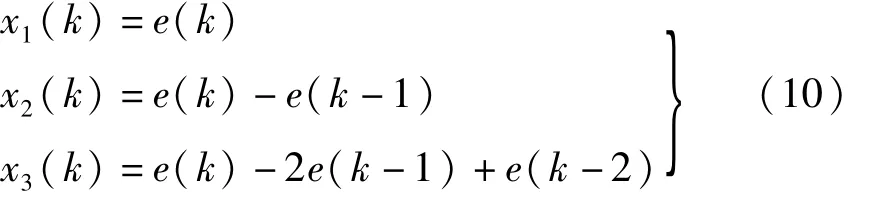
神经元输出u(k)
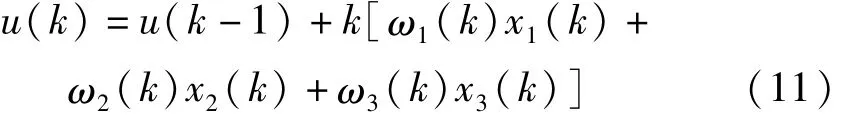
上式中 k为神经元的比例系数,k>0,w1(k)、w2(k)、w3(k)为神经元对 x1(k)、x2(k)、x3(k)的权重系数。权重系数的调整规则见文献[16]。
通过式 (11)和式(7)相位差的计算公式可以求得电机两相的相位差,对应的主程序流程如图13所示。
3 实验结果分析
由于电机运行过程中容易产生位移抖动现象,会产生较大的误差变化率,因此在神经元PID控制算法里假定w3=0,即采用PI调节。
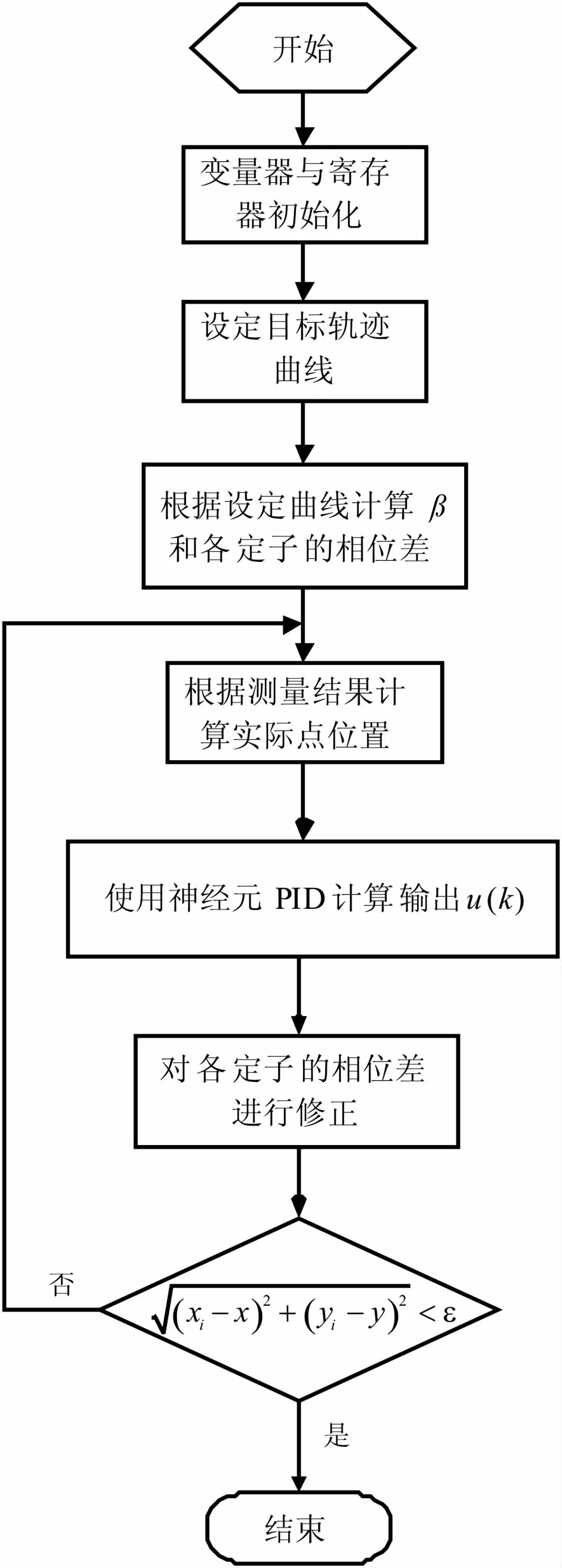
图13 主程序流程图Fig.13 Themain program flow chart of software
图14是闭环控制下β与相位差的变化情况,其中β设定为60°。从图14(a)可以看到,闭环控制下,稳定后的β为59.88°,稳定时间大约为0.8 s。其中各定子两相相位差的变化情况如图14(b)所示。随着时间的增加,定子1两相相位差先增大后减少,定子2两相相位差先减少后增加,定子3两相相位差基本保持不变。
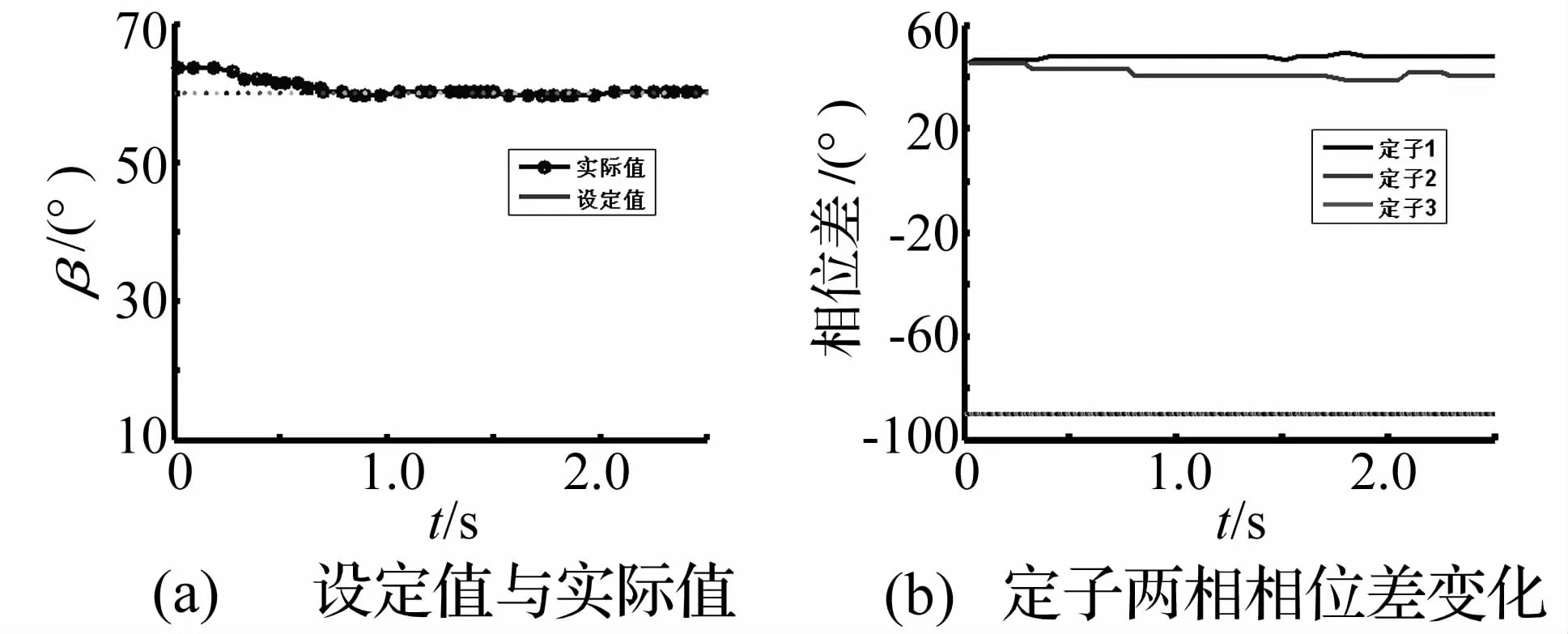
图14 电机闭环运行情况Fig.14 Case when closeloop control
图15是设定目标位置后电机的闭环控制曲线。从图中可以看到,在闭环控制中,电机运行曲线基本上能够跟踪设定曲线,从而实现较好的轨迹跟踪控制。
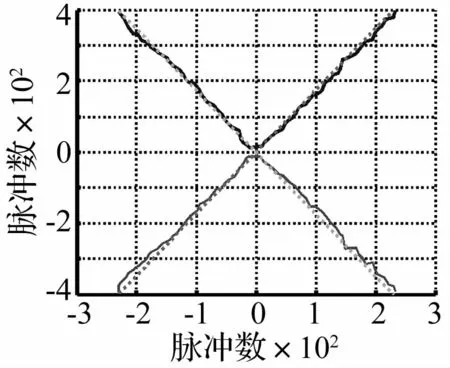
图15 闭环控制曲线Fig.15 Trajectory ofmotion when closeloop control
表2是轨迹闭环控制时的情况。从表2可以看出,闭环控制下电机x轴和y轴的脉冲位置误差控制分别控制在2个脉冲以内,由于我们使用的码盘齿数较少,使得对应x轴和y轴的角度误差绝对值在0.8°以内。若使用码盘齿数更多的编码器,则可以达到更高的精度。
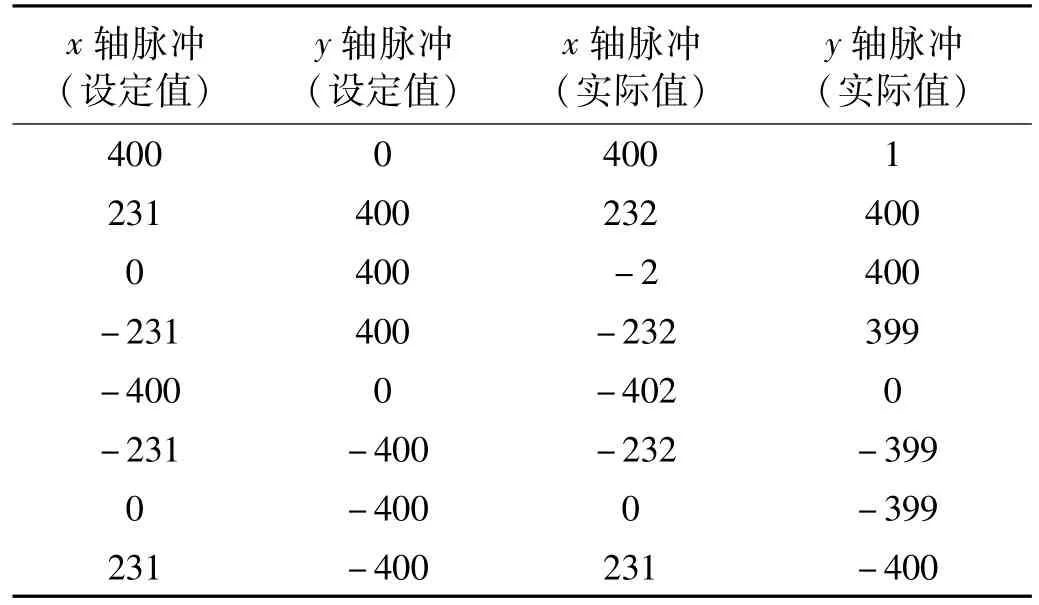
表2 闭环控制情况Tab.2 Closeloop control
若设定电机沿四边形直线运动,四边形的位置(以脉冲计数)分别为(-100,-100),(100,-100),(100,100),(-100,100),电机运动时实际的位置分别为(-99,-98),(99,-98),(99,99),(-98,98),得到的实际运动轨迹如图16所示。图中可以看到实际运动轨迹的位置误差控制在2个脉冲以内,误差不超过2%,可实现较好的轨迹跟踪。
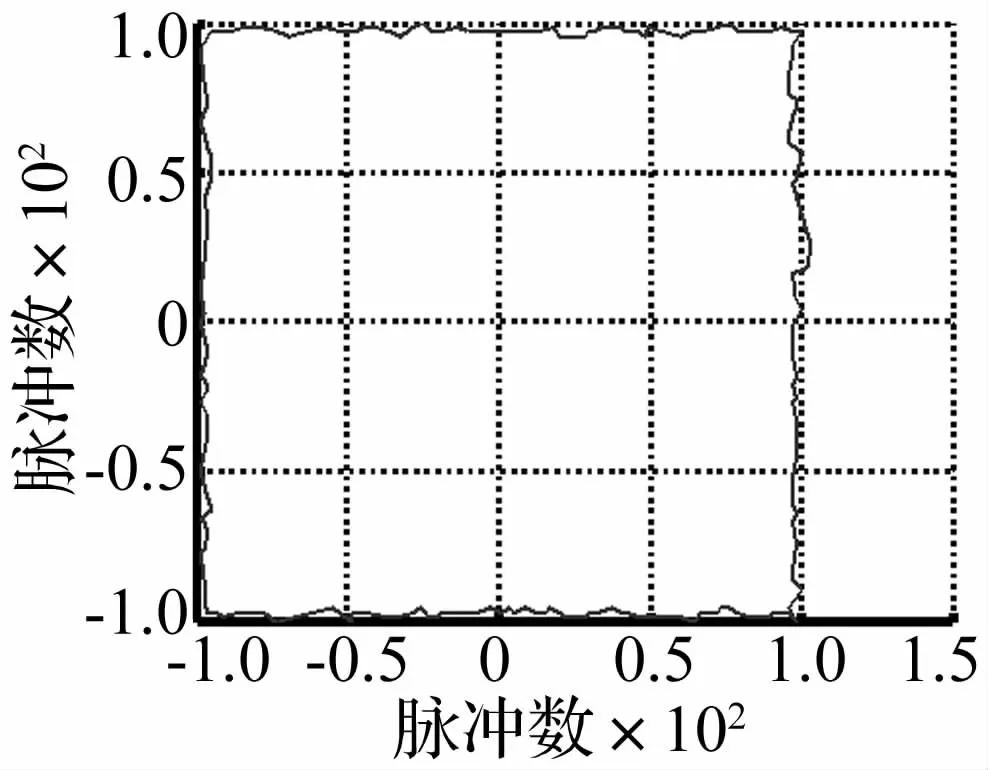
图16 四边形轨迹Fig.16 Quadrilateral trajectory ofmotion
4 结 论
本文通过分析转子运动矢量和x轴夹角β与定子相位差的对应关系,提出了一种二自由度超声波电机的轨迹控制策略。实验证明使用神经元PID控制方法对电机实行轨迹闭环控制后,电机运行曲线对应的x轴和y轴的角度误差控制在2个脉冲以内。
本文提出的轨迹控制方法不仅为多自由度超声波球电机的姿态控制奠定了基础,而且为多自由度超声波球电机的位置/速度伺服研究提供了一种思路。
[1]郭吉丰,傅平.多自由度球形超声波电机的研究进展[J].电工电能新技术.2005,24(2):65-68.GUO Ji-feng,FU Ping.The research progress ofmulti-degree of freedom ultrasonic motor[J].Adv.Tech.of Elec.Eng.&Energy,2005,24(2):65-68.
[2]Mashimo T,Awaga K,Toyama S.Development of a spherical ultrasonic motor with an attitude sensing system using optical fibers[J].IEEE Inter.Conf.on Robotics and Automation,2007:4466-4471.
[3]Purwanto E,Toyama S.Developmentof an ultrasonicmotor as a fine orienting stage[J].IEEE Trans on Robo.and Auto.,2001,17(4):464-471.
[4]Shigeki T,Zhang Guo-qiang,Osamu M.Development of new generation spherical ultrasonic motor[C].Proc.of the 1996 IEEE Inter. Conf. on Robotics and Automation.Minneapolis,1996,3:2871-2876.
[5]河井元良.超音波リニアアクチユエ一ㄆを用いた三自由度球面モ一ㄆの研究[J].精密工学会志,1993,60(3):405-410.Motoyoshi Kawai.Research of aspherical motor with 3 DOF driven by ultrasonic linear actuators[J].JSPE,1993,60(3):405-410.
[6]佐佐江启介.3自由度小型アクユエ一ㄆの开发(第3报)[J].精密工学会志,1996,62(4):599-603。Keisuke Sasue.Development of a small actuator with 3 DOF[J].JSPE,1996,62(4):599-603.
[7]AoyagiM,Beeby SP,White N M.A novelmulti degree of freedom thick-film ultrasonic motor[J].IEEE Transactions on Ultrasonics,Ferroelectrics and Frequency Control,2002,49(2):151-158.
[8]Chen Qiang, Hu Min-qiang, Jin Long, et al. Force transmission model of a cylindrical linear ultrasonic motor[C].Proceeding of International Conference on Electrical Machines and Systems 2007,Oct.8-11,Seoul,Korea:1623-1628.
[9]Takemura K,Maeno T.Design and control of an ultrasonic motor capable of generating multi-dof motion[J].IEEE/ASME Transactions on Mechatronics,2001,6(4):499-506.
[10]胡锡幸,郭吉丰,傅平,等.2自由度球形行波型超声波电动机的特性计算模型[J].机械工程学报,2009,45(3):229-233.HU Xi-xing, GUO Ji-feng,FU Ping,et al. Mechanical characteristics calculation of 2DOF spherical traveling-wave ultrasonic motor[J].Journal of Mechanical engineering,2009,45(3):229-233.
[11]傅平,郭吉丰,沈润杰,等.二自由度行波型超声波电机的驱动和运动姿态控制[J].电工技术学报,2008,23(2):25-30.FU Ping,GUO Ji-feng,SHEN Ren-jie,et al.Driving circuit and position control system of two degree of freedom spherical travelingwave type ultrasonicmotor[J].Transactions of China Electrotechnical Society,2008,23(2):25-30.
[12]傅平,郭吉丰,沈润杰.球形行波型超声波电机的驱动数学模型[J].中国电机工程学报,2006,26(23):115-119.FU Ping,GUO Ji-feng,SHEN Run-jie.The drivingmathematic model of spherical traveling-wave type ultrasonic motor[J].Proceedings of CSEE,2006,26(23):115-119.
[13] Lee K M,Zhou De-bao.A real-time optical sensor for simultaneousmeasurementof three-DOFmotions[J].IEEE/ASME Transactions on Mechatronics,2004,9(3):499-507.
[14]Mashimo T,Awaga K,Toyama S,Developmentofa spherical ultrasonic motor with an attitude sensing system using optical fibers[C].2007 IEEE Inter.Conf.on Robotics and Auto.,Roma,Italy,April 10-14,2007,4466-4471.
[15]胡锡幸,郭吉丰。3个行波定子的2自由度球形超声波电机[J].中国电机工程学报,2010,30(9):62-67.HU Xi-xing,GUO Ji-feng.Two degree of freedom spherical ultrasonic motor with three traveling-wave stators[J].Proceedings of the CSEE,2010,30(9):62-67.
[16]傅平,郭吉丰,丁敬,等.基于神经元自适应PID的超声波电机速度位置控制[J].电工技术学报,2007,22(2):28-33.FU Ping,GUO Ji-feng,DING Jin,et al.A neuron adaptive PID-based speed and position control for ultrasonicmotor[J].Transactions of China electrotechnical society,2007,22(2):28-33.

