考虑打滑现象的振动压路机振动轮的滞回响应特性研究
郑书河, 林述温
(1.福建农林大学 机电工程学院,福州 350002;2.福州大学 机械工程及自动化学院,福州 350108)
振动压路机通过振压将振动能传递给被压实物料,减小物料的变形抗力,增加流动性,提高压实程度及效率,广泛用于道路工程、土建等大型基础施工中。诸如拌合土、碎石、沥青混泥土等施工物料,振压过程中均会产生较大的塑性变形,即在周期载荷作用下,物料的滞回恢复力与物料的位移之间形成一个滞回环[1]。振动压路机在水平激振模式下,由于物料在水平方向上产生相同的弹塑性变形,物料的滞回恢复力与物料的变形位移之间形成一个对称的滞回环[2],由于对称滞回特性的影响,使得振动压实系统成为一个复杂的非线性系统,其动态响应也不再具有线性叠加的简单性。随着压实的进行,土壤的密实度增大,当振动轮受到土壤的压实反力超过最大静摩擦力时出现振动轮与土壤脱耦的打滑现象[3],这时必须建立新的动力学模型反映这种变化。
滞回非线性的研究主要集中在建模和求解两个方面,可以采用分段直线、曲线拟合或微分形式建模[4-5],由于微分模型将滞回恢复力与相对变形位移的关系表示为微分形式,不便于系统非线性解析及工程运算,曲线建模则存在模型过于复杂以及参数冗余等缺点[6-7]。本文采用一种仅依据土壤特性参数的对称分段滞回模型,考虑振动轮在水平激振下既水平振动又绕其圆心摆转的运动情形,根据压实力的大小判断振动轮是否发生打滑现象,建立二自由度动力学模型,利用数值仿真分阶段研究压实进程中振动轮的非线性滞回响应特性,为压路机的设计和施工作业中合理配置工作参数提供理论依据。
1 水平对称滞回模型
振动轮在未发生打滑情况下始终与物料保持接触,物料受到周期作用力,忽略参数的慢变,物料的滞回恢复力如图1,在第一周期内,振动轮向右运动,物料进入弹性变形,设初始刚度为k1,达到屈服极限开始塑性变形阶段A-B,由于塑性变形量很小,分析时可忽略,继续加载至右向运动极限点B后,振动轮开始向左运动进入反向卸、加载阶段B-C,反向达到屈服极限点C后,继续加载阶段C-D,当到达反向运动极限点D后,又进入新的加载阶段D-E,由于计算每一个周期内恢复力都以上一个周期反向卸载终止点为下一个周期的起点,且左右方向加、卸载时物料产生相同的弹塑性变形,故恢复力与位移形成封闭的对称滞回环。

图1 双线性对称滞回模型Fig.1 Bilinear symmetrical hysteresismodel
据上述模型,滞回恢复力zh可表示为:
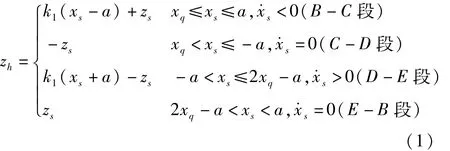
式中,a为振动轮作用下物料的振幅,xs为物料的水平位移,k1、xq依次为物料的屈服刚度系数和屈服极限,zs为物料屈服时产生的滞回力,显然zs=k1xq,xc=a-2xq,xB=a,xD= -a,xE=2xq-a。
2 二自由度动力学模型
智能振动压路机基于水平振动和垂直振动为一体的振动模式,根据道路的不同压实状况调整振动模式,用于各种路基和路面土方的压实。现研究在水平激振模式下,即激振角α=0,由于压路机前后轮激振模式按对称布置,即前后轮水平激振力大小相等,方向相反,机架与驾驶室的振动位移为零可忽略[8],假设振动轮与地面接触不打滑,取静平衡位置为零点,由于振动轮在驱动力矩作用不断向前滚动的,假设振动轮下一次加载时接触的是未发生变形新的土壤,土壤的塑性变形量没有记忆,认为振动轮回到静平衡位置,振动轮受到土壤的滞回力与土壤变形就形成一个滞回环,并可忽略水平驱动推力对振动轮滞回特性的影响,振动轮与物料滞回恢复力采用图1滞回模型,前后振动轮的振动特性基本类似,采用单一振动轮形式,如图2,建立如下动力学方程:
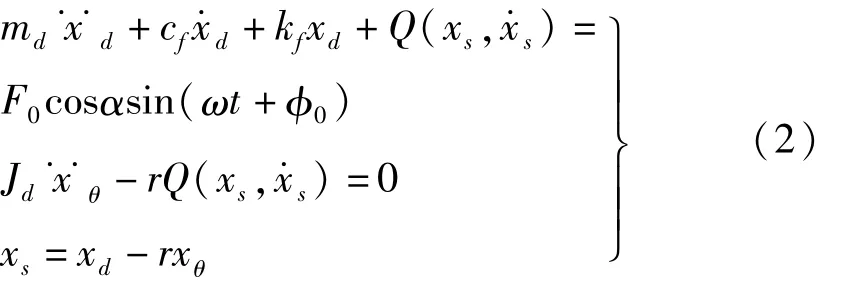
式中,md,Jd依次为振动轮质量和转动惯量,ms为随振物料的质量较小可忽略。xd,xθ依次为振动轮水平、转动位移,kf,cf依次为机架减震器刚度系数和阻尼系数,为物料的作用力,包含瞬时力项滞回力项 qhy(xs),可表示为[9]:
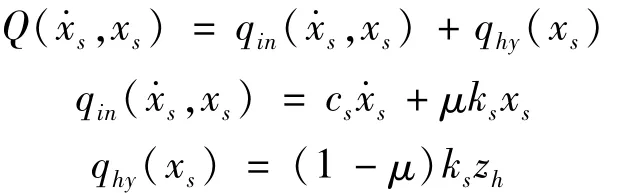
式中:μ为屈服前后物料刚度之比,F0为激振力幅值,ω为激振频率,Ф0为激振力初始相位角,ks,cs依次为压实土壤的瞬时水平刚度系数和阻尼系数。
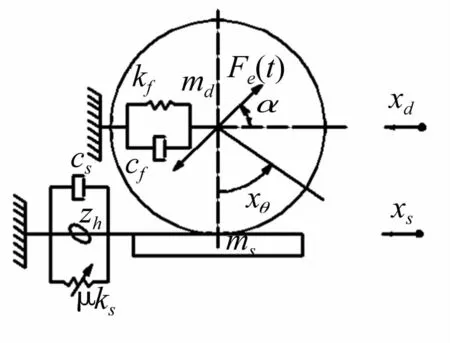
图2 压实系统动力学模型Fig.2 Dynamic model of vibratory compaction system
对于非线性作用力采用等效线性法
表示:

首先假设一次近似解:
例如:在进行准备活动的时候,老师可以使用称为“呼叫动作”的游戏而不是体操,这样比传统的准备活动更加生动有趣。它可以更有效地调动学生参与的激情,从而改善大脑中枢和身体器官的活动水平,提高准备过程的有效性。而体育比赛小游戏在体育热身部分的融入可以改善热身单一化的现状,使学生对体育知识和运动更感兴趣。例如,在教学有关长跑的时候,学生想到1000米、800米等概念,他们就很容易害怕,而且他们的腿会发软。此时,可以使用各种模式快慢跑的组合,快速和慢速跑步以及交替变换的形式,促使学生在生动有趣的游戏中无意识地学习新的运动技能。
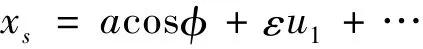
图1中,近似地假设B-C,C-D,D-E,E-B四线段对应的相角的范围为:0~Фc,Фc~π,π~ФE,ФE~2π。其中xC=a-2xq,xE= -a+2xq。则按谐波线性法,非线性作用力的等效阻尼、等效刚度依次为:

方程式(5)在形式上为二自由度线性振动系统,利用线性理论可得稳态解。
由图2可知,振动轮与土壤接触不打滑时,振动轮对土壤水平方向施加的压实力Fs,即摩擦反力可得:

同时,摩擦反力Fs也满足:

式中,fs为振动轮受到土壤面层的摩擦力,取值范围是0~fmax,fmax为最大静摩擦力。压实初期,土壤刚度阻尼系数较小,振动轮施加土壤的压实力较小,满足|Fs|<fmax,振动轮处于接触耦合振压阶段,系统的动力学模型符合式(1)~(5),随着压实的进行,土壤进入半密实状态并逐渐过渡到密实状态,当摩擦反力Fs逐渐增大至fmax时,振动轮与土壤面层发生脱耦,进入打滑阶段。打滑时土壤摩擦力应等于动摩擦力,即摩擦副相对滑动速度的函数。考虑振动轮水平振动的平均速度0.06~0.1 m/s较小,故将打滑摩擦力近似一个常数为最大静摩擦力fmax。因此,打滑阶段振动轮在水平方向受到机架约束力、土壤动摩擦力、激振力的作用下运动,而其摆转方向受到静摩擦力矩的作用,产生一脱耦阶段的加速运动,可列出如下动力学方程:

式中,sign(x)为符号函数,Ф1为振动轮发生打滑时激振力初始相位角。
3 算例仿真
以福州大学与厦工集团三重公司联合研制的XG6133D型智能振动压路机为例,已知:md=3 000 kg,α=0,参考现有压路机实验结果和本机构件的特点,具体选取参数如下:

3.1 土壤刚度及阻尼系数的影响
对于压实初期土壤刚度较小,阻尼较大的情况下取:
随着压实的进程,土壤逐渐密实,土壤刚度增大,阻尼减小,此时土壤只吸收较小的能量,发生较小的塑性变形,压实中期、后期土壤刚度系数分别取6、8 MN·m-1,阻尼系数分别取 80、50 KN·s·m-1,屈服极限依次为0.003、0.005 m,激振力幅和激振频率不变,仿真如图4~5,从图可看出:随土壤逐渐密实,振动轮水平及摆振运动振幅增大,水平运动的谱图开始出现亚谐波共振,当到了压实后期,压实力超过最大静摩擦力时,振动轮与土壤面层发生脱耦打滑,振动轮发生亚、超谐波共振,呈现以基波为主含有明显的各次亚、超谐波成分的频谱,其超谐波频谱中出现较小的明显偶次倍谐波,标志着打滑现象的发生,偶次倍谐波可认为在打滑阶段,由于摆转运动是一依赖初始速度下的脱耦加速运动,从而导致随振土实际的水平位移左右不对称而呈现的非线性滞回特性。Poincare截面图上不动点集从压实初期的点状逐渐发展成条状,表明振动轮水平运动从能量集中的频谱逐渐转变为以基波为主含各倍次能量均匀谐波谱,振动轮作稳定的水平倍周期运动。
3.2 激振力幅和激振频率的影响
考虑振动压路机在工作时可调整激振力幅、激振频率等工作参数,考察工作参数的变化对系统动力学特性的影响,取压实进程的中期,保持土壤的参数、激振力幅不变,增大激振频率,仿真如图6、7。比较图4、6、7图中可得:随着激振频率的增大,阻尼的作用,振动轮水平振动和摆振幅值大幅度下降,频谱呈现以基波为主含明显的各高奇次倍谐波特性,谱能量集中于基波处并沿高奇次倍谐波处延续。

图3 压实初期振动轮响应图Fig.3 Response of vibratory drum in initial compaction stage

图4 压实中期振动轮响应图Fig.4 Response of vibratory drum in middle compaction stage

图5 压实后期振动轮响应图Fig.5 Response of vibratory drum in latter compaction stage

图6 激动频率f=30 Hz时振动轮响应图Fig.6 Response of vibratory drum at30 Hz

图7 激振频率f=40 Hz时振动轮响应图Fig.7 Response of vibratory drum at40 Hz
取压实进程的后期,保持土壤参数、振频不变,设激振力幅F0=50、160 kN两档激振力幅,仿真如图8、9。比较图5、8、9可得:随着激振力振幅的增大,打滑现象加剧,打滑阶段时间加长,频谱呈现不仅明显的偶次倍谐波成分,而且增加了分数倍的亚谐波和超谐波成分,谱能量愈发向各次倍谐波处分散。Poincare截面图上不动点集从条状演化成网状,振动轮水平运动从稳定的倍周期运动进入拟周期运动,但频谱图依然呈现离散谱,系统不进入混沌运动。
可见随着压实的进程,土壤的逐渐密实,振动轮将在压实土壤面上产生脱耦打滑,随着激振力的增大,脱藕打滑阶段提前,打滑程度加剧,振动轮运动愈发复杂,当增大激振频率时,会使振动轮位移响应值减低,减小激振力,一定程度可抑制打滑现象的产生。因此,压实的后期,为了保证压实质量和效率,可采用低幅高频的激振参量,减缓脱耦打滑程度,使得振动轮频谱响应呈现基波为主含各倍次能量均匀谐波谱,振动轮维持稳定的倍周期运动,如仿真图10。

图8 激动力F0=50 kN时振动轮响应图Fig.8 Response of the vibratory drum under 50 kN amplitude of excitation force

图9 激振力F0=160 kN时振动轮响应图Fig.9 Response of the vibratory drum under 160 KN amplitude of excitation force

图10 低振幅高频激振下振动轮响应图Fig.10 Response of the vibratory drum in low excitation force and high excitation frequency
4 结 论
提出一种可以反映压实进程中土壤弹塑性变形的对称滞回模型,并考虑压实进程中振动轮发生脱耦打滑现象,分阶段建立包含对称滞回模型的动力学模型,通过数值仿真分析发现:
(1)土壤弹塑性变形阶段,由于对称滞回力的非线性作用,使得振动轮波形发生畸变,频谱以基波为主仅含高奇次倍谐波分量。
(2)随着土壤刚度和阻尼的变化,压实中期振动轮在土壤面层产生脱耦打滑,振动轮发生亚、超谐波共振,频谱中出现微小的偶次倍谐波,随土壤进一步密实,脱耦打滑加剧,频谱增加了明显的分数倍亚、超谐波,标志了打滑现象的发生,谱能量均匀分散,振动轮从倍周期运动进入复杂的拟周期运动。当增大激振频率时,振动轮的位移响应值减小,振动轮脱耦打滑现象减缓;当增大激振力幅,打滑现象加剧,振动轮愈早进入拟周期运动。
(3)振动轮在土壤面层发生脱耦打滑将影响到压实质量和压实效率,通过减小激振力和增大激振频率,可抑制脱耦打滑现象,避免拟周期运动的产生,这为压路机的设计和施工作业中合理配置工作参数提供理论依据。
[1]Ayoub A.Seismic analysis of wood buiding structures[J].Engineering Structures,2007,29(2):213-223.
[2]SHEN Pei-hui,LIN Shu-wen. Mathematic modeling and characteristic analysis for dynamic system with asymmetrical hysteresis in vibratory compaction[J].Meccanica,2008,43(5):505-515.
[3]孙祖望,卫雪莉,王鹊.振荡压实的动力学过程及其响应特性的研究[J].中国公路学报,1998.4,11(2):117-126.SUN Zu-wang,WEI Xue-li, WANG Que.The dynamic process of oscillatory compaction and its response characteristics[J].China Journal of Highway and Transport,1998,11(2):117-126.
[4]Okuizumi N,Kimura K.Multiple time scale analysis of hysteretic systems subjected to harmonic excitation[J].Journal of Sound and Vibration,2004,272(3-5):675-701.
[5]Jin J D,Zhang Y F,Wei W.Steady-state response of a binon-linear hysteretic system[J].International of Journal of Non-linear Mechanics,2006,41(8):926-935.
[6]Mohamed Husain,Panos Tsopelas.Measures of structural redundancy in reinforced concrete buildings I:redundancy indices[J].Jourmal of Structural Engineering,2004,130(11):1651-1658.
[7]Ma F,Zhang H,Bockstedte A,et al.Parameter analysis of the differential model of hysteresis[J].Journal of Applied Mechanics,2004,71(3):342-349.
[8]郑书河,林述温.模式可调智能振动压路机动力学特性的建模与仿真[J].福建农林大学学报(自然科学版),2011,40(6):657-663.Zheng Shu-he, Lin Shu-wen. Dynamic characteristics modeling and simulation of intelligent vibratory roller with adjustable vibration mode[J].Journal of Fujian Agriculture and Forestry University(Natural Science Edition),2011,40(6):657-663.
[9]Wang C H,Chang S Y.Development and validation of a generalized biaxial hysteresis model[J]. Journal of Engineering Mechanics,2007,133(2):141-152.
[10]韩清凯,闻梆椿.一种不对称滞回受迫振动系统及其分析[J].振动工程学报.1998.9.11(3):291-296.HAN Qin-kai, WEN Bang-chun. Analysis of a forced vibration system with asymmetrical hysteresis[J].Journal of Vibration Engineering,1998,11(30):291-296.

