基于碰撞振动的隔振系统混沌化实验研究

俞 翔，朱石坚，楼京俊

（海军工程大学 科研部，武汉 430033）

针对舰船水下辐射噪声中的低频线谱直接危害舰船安全、制约战斗力且难以消除的问题，朱石坚等［1－9］提出了舰船水下辐射噪声线谱混沌化控制方法，即设计强非线性隔振系统，并通过施加适当控制，使系统处于持续的混沌运动状态。此时混沌系统具有的线谱输入、宽频连续谱输出特性，可实现对水下辐射噪声的频谱重构，有效削弱线谱特征，隐匿线谱所携带的潜艇信息。目前，线谱混沌化控制方法在原理验证、混沌区域计算、隔振性能评估、混沌实验识别、控制算法等方面取得了诸多成果，但在工程应用等方面还存在着若干难点，其中之一就是如何在隔振系统小振幅下实现较宽频率范围内的混沌。针对该难点，本文提出了基于碰撞振动的隔振系统混沌化控制方法，即在线性隔振系统中引入由两碰撞质量块组成的附加子系统，在恰当的参数设置下，碰撞子系统能产生混沌运动，通过子系统与隔振系统之间的耦合，可以使得隔振系统也呈现出混沌运动状态，并且附加子系统的引入能有效抑制被隔振设备的振动和降低传递到基座的线谱强度。碰撞振动具有强非线性特性，呈现出丰富的动力学行为，吸引了大量的学者开展研究［10－13］。本文构建实验系统对该方法进行详细研究，验证了其有效性，并得到系统混沌频率范围及随其它参数变化的若干规律。

1 系统模型

船舶动力机械隔振系统采用的隔振器种类众多且技术成熟，本文在不对隔振系统作过多改动的前提下，引入附加碰撞系统，以期在隔振系统振幅较小的情况下也能在较宽频率范围内产生混沌运动。实验系统如图1（a）所示，1为激振器，它通过顶杆9和连接器与隔振系统负载（板3、10）连接；滑柱2与隔振系统负载（板3、10）的通孔构成滑配，其作用为保证隔振系统只作竖直往复运动；隔振系统负载之下的隔振元件4为4个B3－25型船舶通用隔振器，该型隔振器为线性隔振器，它们通过圆柱形垫块6连接于凹形托架7之上；凹形托架之下为75型橡胶隔振器14，其作用为模拟基础的柔性，要求其刚度远大于隔振系统中隔振元件4的刚度，以使凹形托架7及75型隔振器14可视为隔振系统的柔性基础；工作圆台8通过螺栓与整个实验装置的底座15固连，底座15的质量远大于其上的各个部件，因而可视为刚性底座。

以上为实验装置的线性隔振系统部分，在此基础上，引入了由13碰撞质量块m2、5弦、12碰撞质量块m1、11支柱组成的附加碰撞振动子系统，该子系统的详细结构如图1（b）所示。m2由上下两个平板组成，上下板的内表面构成碰撞面，两板之间的距离D可以调节，m2通过弹簧连接在隔振系统负载板上，该弹簧横向刚度较大，可认为碰撞块m2仅作竖直方向的运动。另一个碰撞块m1位于m2上下两平板之间，由一个两侧面开槽的钢质立方体构成，它通过两根弦连接在两个支柱上，支柱固定连接在隔振系统负载板上，从而可以通过调节支柱间的距离控制弦的预拉力。当隔振系统受到激励时，隔振系统负载板将带动子系统一起振动，若参数设置适当，m1与m2之间便会产生碰撞振动，并引发混沌运动，碰撞产生的力又会通过弹簧和弦作用于隔振系统，从而使得隔振系统呈现出混沌特性。m1与其连接弦为非线性系统，其刚度特性为［7］：式中，S为预拉力，k为弦的拉伸刚度，l为单根弦的长度。在本实验中，通过控制其预拉力S来实现系统在不同频率范围内的碰撞。

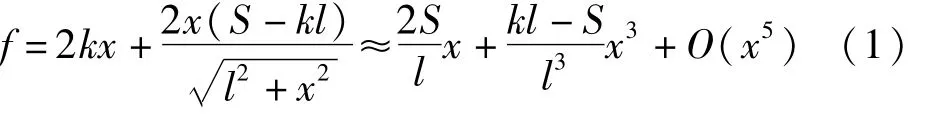
2 实验装置

构建的实际物理实验装置，如图2所示。传感器的布置如图2所示，在隔振系统负载上、基座以及碰撞质量块m2上各布置一个ICP加速度传感器；在激振器顶杆与隔振系统负载之间布置一个压电式力传感器；在碰撞质量块m2下安装一个激光位移传感器。

图2 实验装置与数据采集系统Fig．2 Experimental setup and data acquisition system

对实验装置中的各参数进行了参数识别，具体数值参见表1。本实验研究可以改变的系统参数为激励力频率H、激励力幅值P、碰撞块m2上下板之间的距离D以及弦的预拉力S，因此参数组（H，P，D，S）可以用作实验数据的标识。

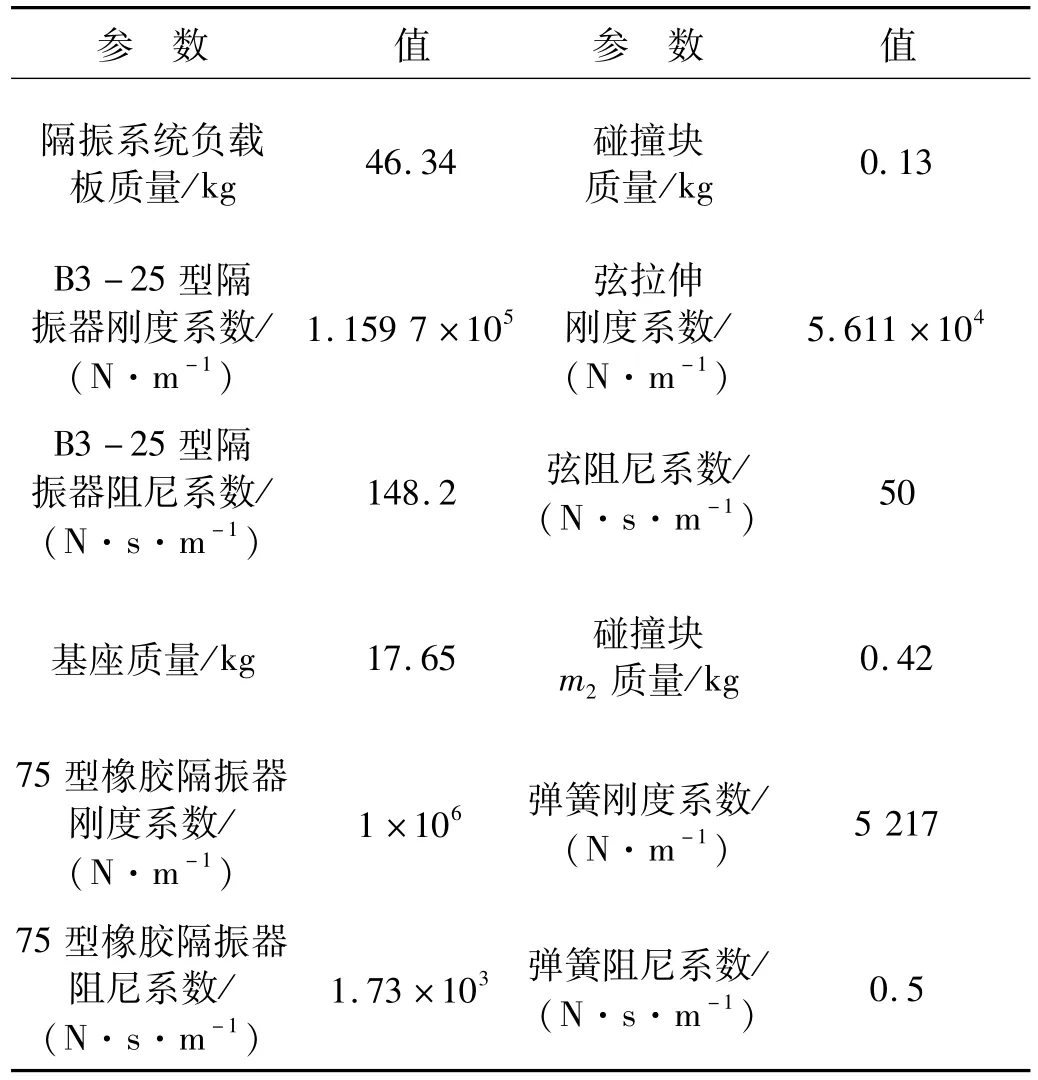
表1 实验系统参数Tab．1 Param eters of the experim ental setup

3 实验步骤

本实验为正弦信号的慢速频率扫描实验，扫频范围为 14 Hz～18．5 Hz，步长为 0．1 Hz，采样频率为 500 Hz，数据采集时长为5 s。

完成各参数组下的频率扫描实验后，对实验数据进行后处理。实验数据的处理基本按照非线性时间序列分析方法来进行，首先需要解决的是实验信号的混沌识别。

4 实验数据与分析

4.1 混沌实验识别

对于振动实验系统，可以利用时间历程图、相图、位移信号功率谱密度图、Poincaré图以及关联维和Lya-punov指数等综合判断一个系统是否处于混沌运动状态［7］。

首先针对2组实验参数：1）P＝60 N，H＝15．5 Hz，D＝36．2 mm，S≈7 0 N；2）P＝60 N，H＝16．1 Hz，D＝36．2 mm，S≈7 0 N下的信号进行识别。图3所示为两组参数下，碰撞块m2竖直方向的位移信号与加速度信号时间历程图、位移信号的功率谱密度图（以1 mm为参考值）、相空间重构吸引子图。并用G－P法［8］计算两组参数下位移信号的关联维数，用Wolf方法［9］计算最大 Lyapunov指数。

从图3（a）上看出每碰撞一次，加速度信号便出现一个脉冲信号，脉冲信号的出现并不呈现周期性，位移信号也找不到任何周期性变化规律，其功率谱为连续谱，重构吸引子相图和Poincaré图也呈现出混沌吸引子典型的相轨迹拉伸、折叠特征。计算得到该参数组下，系统的关联维数为3．309 3，最大 Lyapunov指数为0．030 2，综合上述判据，可以得出参数组1下的系统运动为混沌运动。

从图3（b）上可以看到，加速度信号中脉冲的出现呈现周期性，基本为3个激励周期碰撞两次，位移时间历程曲线及其功率谱密度图、重构吸引子及其Poincaré图也表现为典型的1／3次谐波特征，计算得到该参数组下，系统的关联维数为1．077 3，最大Lyapunov指数为－0．004 7，考虑到实验信号中含有的噪声以及计算误差，可以认为该参数组下对应信号具有整数关联维数1，因此可以判断出该参数组下系统运动为1／3次谐波周期运动。

4.2 分岔特性分析

上小节选取了两组具有代表性的信号进行了混沌识别研究，下面根据上述混沌识别方法对系统分岔特性进行分析，得出系统混沌频率区域随可变参数（P，D，S）的变化规律。Poincaré截面取为 Σ＝｛（xn，…，xn＋mτ）｜xn＋τ＝0，xn＞0｝，根据 Poincaré映射得到分岔图。

图3 碰撞块m2竖直方向的位移、加速度时间历程图、位移功率谱图和重构吸引子图Fig．3 Time histories of the displacements and accelerations，power spectra and reconstructed attractor of the displacements of m2 in gravity direction

图4 系统随激励频率变化的分岔图Fig．4 Bifurcation diagrams varying with the excitation frequency

首先分析P＝60 N，D＝36．2mm，S≈70 N时，系统随激励力频率变化的分岔特性，如图4（a）所示。从图上可以看到，系统在15 Hz至17．8 Hz存在碰撞，其中15～15．5 Hz与 16．2～17．8 Hz为两个碰撞混沌运动区域，而15．6～16．1 Hz为碰撞而产生的次谐周期运动区域。5．1节中的参数组1下的运动即位于第一个混沌区域中，而参数组2处于周期运动区域。

固定P＝40 N，S≈70 N，改变碰撞块m2上下板之间的距离D为39．5 mm和34 mm，分别作系统随激励频率变化的分岔图，如图4（b）、（c）所示。从图上可以看到，当D＝39．5 mm时，系统仅在16～16．5 Hz以及17．7～18．1 Hz之间存在混沌运动，这正对应着碰撞对m1、m2子系统各自的共振频率。而当D＝34 mm时，系统混沌区域显著加大，在14．5～18．2 Hz整个碰撞区域，除了15．5～16 Hz有较小的周期窗口外，其余均为混沌运动区域。

由上述分析可以得到：① 激励力幅值P的增大能加大产生混沌的频率范围；② 碰撞块m2上下板之间的距离D减小有利于增大产生混沌频率范围。

4．3 振动特性分析

还需对隔振系统负载板的振幅进行研究，进而验证碰撞质量块能在隔振系统振幅较小的情况下实现较强的混沌运动。

在实验过程中，由于条件所限，并没有对隔振系统负载板以及基座的位移进行测量，因此只能根据测量得到的加速度信号来估算系统的振幅。对于简谐运动x＝A sin（ωt），其加速度x··也为正弦信号：x··＝B sin（ωt）＝－ω2A sin（ωt），由此可见位移信号幅值与加速度信号均方根值之间的关系为：Arms＝Brms／ω2，该关系式不适用于混沌运动，因此只能估算混沌区域前后周期运动的位移幅值。根据理论分析，混沌运动时，隔振系统负载板的位移幅值处于混沌区域前后周期运动位移幅值之间，因此，也可以大致确定出混沌运动时，隔振系统负载板的位移幅值。

对于P＝60 N，D＝36．2 mm，S≈70 N时的情况，根据图4（a）选取H＝14 Hz计算隔振系统负载板加速度均方根值可得1．30 m／s2，因此可估算得到位移均方根值为：0．17 mm；选取 H＝18．3 Hz计算隔振系统负载板加速度均方根值为0．92 m／s2，估算可得位移均方根值为0．07 mm，由此可见，混沌运动时，隔振系统负载板的位移均方根值应处于0．07～0．17 mm，该振幅已非常小了。

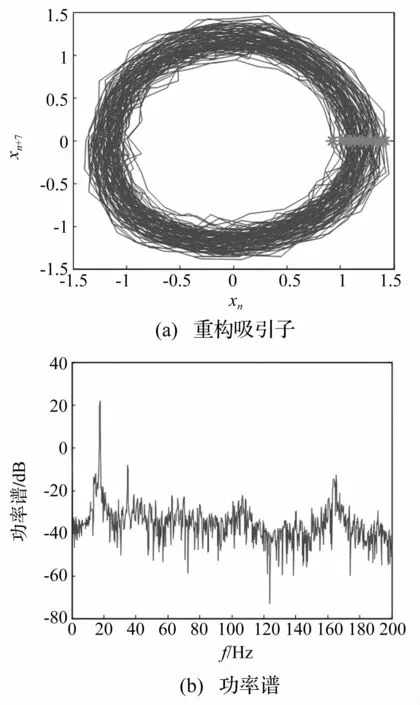
图5 隔振系统负载板的重构吸引子与功率谱图Fig．5 Attractor reconstruction and power spectra of the isolated plates

接下来验证在如此小振幅下，隔振系统仍能呈现出较强的混沌运动。在分岔图4（a）的混沌区域中选择1个典型频率H＝17．5 Hz，图 5为 P＝60 N，D＝36．2 mm，S≈70 N，H＝17．5 Hz时隔振系统负载板的重构吸引子和功率谱，图上“*”为Poincaré映射点。从图上可以看到，在振动幅值相当小的情况下，系统仍然能呈现出显著的混沌运动特征，这进一步说明了基于碰撞质量块的混沌化控制方法的有效性。

4．4 减振性能分析

本实验分析了在图4（a）、（c）情况下，混沌频率范围内系统有无碰撞振动子系统时隔振系统负载板振动加速度情况。如图6所示，图6（a）、（b）分别为激励力幅值P为60 N时负载板的振动加速度均方值与振动减小的相对百分比，图6（c）、（d）为 P等于40 N时的情况，图上实线和虚线分别为有和没有碰撞振动子系统时的曲线。从图6可以看出，当激励力频率小于18 Hz时，附加碰撞振动子系统的引入对隔振系统负载板的振动抑制作用明显，减少的相对量最大可达到了21%。在18～18．5 Hz范围内，碰撞振动子系统的减振作用不明显。而当激励频率大于18．5 Hz时，碰撞振动子系统的引入反而使得隔振系统负载板的振动幅值加大，加剧了被隔振设备的振动。结合分岔图4（a）可以看出，混沌运动区域为14．7～17．9 Hz，因此在混沌运动的绝大部分频率区域中，碰撞子系统的引入均能有效抑制被隔振设备的振动，而在小部分区域振动抑制作用不明显，但也不会加剧其振动。当激励力幅值P为40 N时，也可以得到和P＝60 N类似的结论，如图6（c）、（d）所示。

图6 碰撞振动子系统的减振性能Fig．6 Performance of vibration reduction of the vibro-impact subsystem

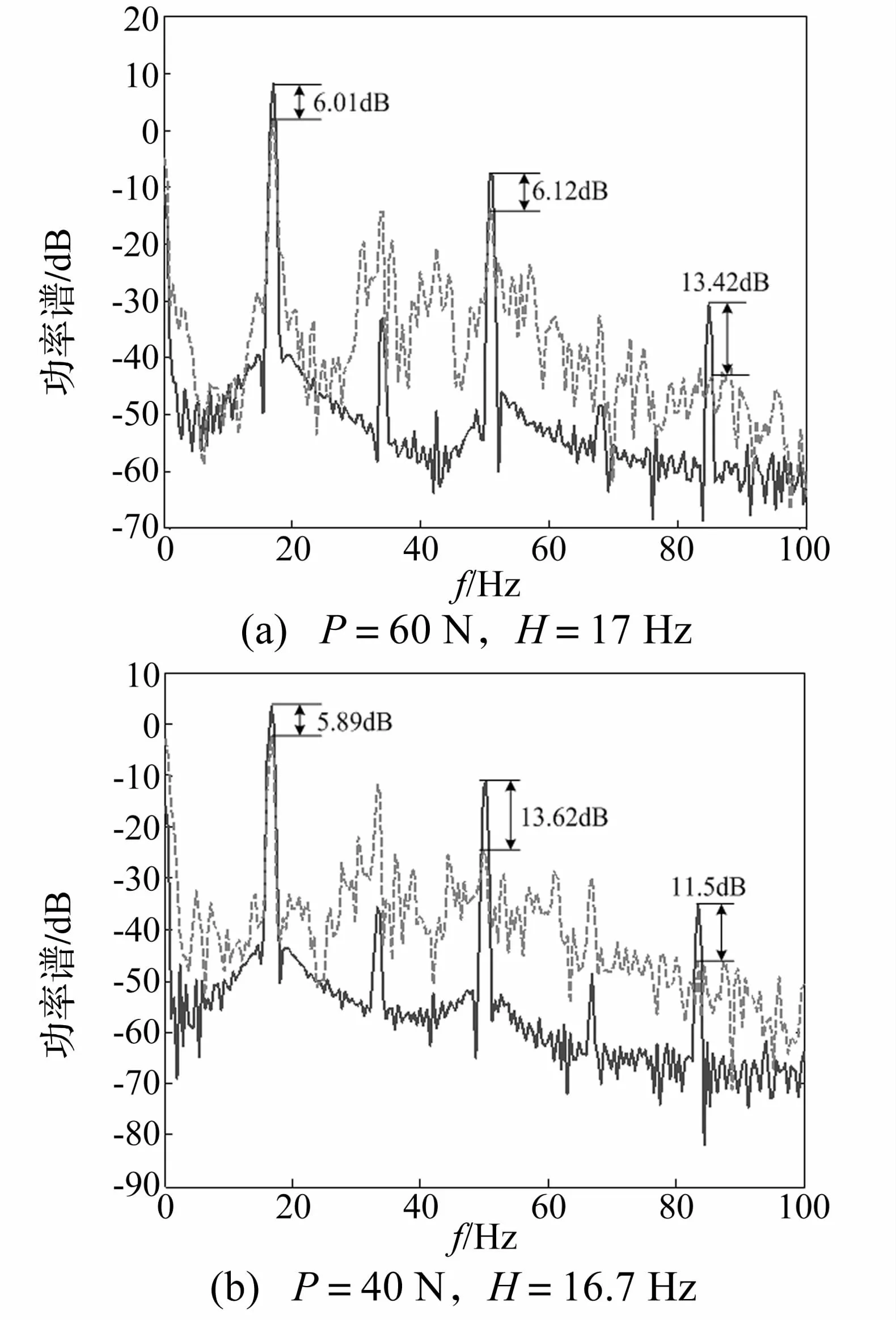
图7 周期运动与混沌运动时基座加速度功率谱Fig．7 Power spectra of the accelerations of the base in periodic and chaotic states

接下来讨论基于碰撞振动的隔振系统混沌化控制方法对线谱的控制效果。图7（a）所示为在P＝60 N，H＝17 Hz的激励情况下，隔振系统周期运动时与引入碰撞振动子系统后使得隔振系统呈现混沌状态时基座加速度功率谱的比较（以1 m／s2为参考值）。实线所示为周期运动时的功率谱图，从图上可以看出，此时系统在激励力频率17 Hz及其倍数51 Hz以及85 Hz处存在较强的线谱成分。虚线为混沌运动状态时的功率谱图，与周期运动的功率谱图比较可以发现，此时三个主要线谱的强度均有不同程度的衰减，其中17 Hz处，线谱降低 6．01 dB，51 Hz处，降低 6．12 dB，而在 85 Hz处，线谱降低幅度达到了13．42 dB。不仅线谱强度得到了降低，整个功率谱的有效值也由于碰撞振动子系统的引入而降低了4．77 dB。

在P＝40 N，H＝16．7 Hz的激励情况下，也可以得到类似的结论，如图7（b）所示，同样实线为周期运动状态下基座的加速度功率谱，而虚线为混沌状态时基座的加速度功率谱（均以1 m／s2为参考值来求得分贝值）。由图上可以看出，16．7 Hz、50．1 Hz以及 83．5 Hz处的三条线谱在混沌状态下分别减少了5．89dB、13．62 dB以及11．5 dB，并且整个功率谱有效值下降了约3 dB。

5 结 论

本文对基于碰撞振动系统的隔振系统混沌化控制进行了实验研究，通过研究表明：在隔振系统中引入碰撞振动子系统，能实现小振幅下较宽频率范围内的混沌运动，并且由于碰撞振动子系统的引入，而能有效抑制被隔振设备的振动。在碰撞混沌发生时，不仅系统传递到基座的线谱强度得到了有效降低，而且其功率谱整体强度有所下降。由此验证了基于碰撞振动的隔振系统混沌化方法的有效性。

［1］朱石坚，姜荣俊，何琳．线谱激励的混沌隔振研究［J］．海军工程大学学报，2003，15（1）：19－22．ZHU Shi-jian，JIANG Rong-jun，HE Lin．Research on the chaos vibration-isolation of line spectra excitation［J］．Journal of Naval University of Engineering，2003，15（1）：19－22．

［2］Lou JJ，Zhu S J，He L，et al．Application of chaosmethod to line spectra reduction［J］．Journal of Sound and Vibration，2005，286（3）：645－652．

［3］俞翔，朱石坚，刘树勇．广义混沌同步中的多稳定同步流形［J］．物理学报，2008，57（5）：2761－2769．YU Xiang， ZHU Shi-jian， LIU Shu-yong． Multi-stable synchronization manifold in general synchronization of chaos［J］．Acta Physica Sinica，2008，57（5）：2761－2769．

［4］俞翔，朱石坚，刘树勇．多自由度非线性隔振系统建模及其非共振响应［J］．振动与冲击，2007，26（7）：69－73．YU Xiang，ZHU Shi-jian，LIU Shu-yong．Dynamic modeling for multi-degree-of-freedom nonlinear vibration isolation system and its nonresonant response［J］．Journal of Vibration and Shock，2007，26（7）：69－73．

［5］楼京俊，朱石坚，何琳．混沌隔振方法研究［J］．船舶力学，2006，10（5）：135－141．LOU Jing-jun，ZHU Shi-jian，HE Lin．Application of chaos method in vibration isolation［J］．Journal of Ship Mechanics，2006，10（5）：135－141．

［6］朱石坚，刘树勇．混沌振动识别的研究［J］．武汉理工大学学报（交通科学与工程版），2003，27（6）：766－769．ZHU Shi-jian，LIU Shu-yong．A study of chaotic vibration identification［J］．Journal ofWuhan University of Technology（Transportation Science＆Engineering），2003，27（6）：766－769．

［7］Li Y L，Xu D L，Fu Y M etal．Stability analysis of vibration isolation floating raft systems for chaotification with time-delayed feedback control［J］．Chaos，2011，21（3）：033115．

［8］Zhang J，Xu D L，Zhou JX，et al．Chaotification of vibration isolation floating raft system via nonlinear time-delay feedback control［J］．Chaos，Solitons＆Fractals，2012，45（9－10）：1255－1265．

［9］Xu D L，Yu Q P，Zhou J X，et al．Theoretical and Experimental Analysis of A Nonlinear Magnetic Vibration Isolator with Quasi-Zero-Stiffness Characteristic［J］．Journal of Sound and Vibration，2013，332（14）：3377－3389．

［10］Babitsky V I．Theory of vibro-impact systems and applications［M］．Berlin：Springer，1998．

［11］金栋平，胡海岩．碰撞振动与控制［M］．北京：科学出版社，2005．

［12］郑小武，谢建华．一类碰撞振动系统的倍周期分岔研究［J］．四川大学学报（工程科学版），2006，38（2）：30－33．ZHENG Xiao-wu，XIE Jian-hua．Study of period-doubling bifurcations of a vibro-impact system［J］．Journal of Sichuan University（Engineering Science Edition），2006，38（2）：30－33．

［13］赵文礼，周晓军．二自由度含间隙碰撞振动系统的分岔与混沌［J］．浙江大学学报（工学版），2006，40（8）：1435－1438．ZHAO Wen-li，ZHOU Xiao-jun．Bifurcation and chaos of impact vibration system with two degrees of freedom and clearance［J］．Journal of Zhejiang University（Engineering Science）：2006，40（8）：1435－1438．

［14］ Grassberger P，Procaccia I．Characterization of strange attractors［J］．Physical Review Letters，1983，50（5）：346－349．

［15］Wolf A，Swift JB，Swinney H L，et al．Determing Lyapunov exponents from a time series［J］．Physica D，1985，16：285－317．