考虑分时电价的多目标批调度问题蚁群算法求解

李小林,张 松,陈华平

（1.中国矿业大学矿业工程学院,江苏徐州 221116；2.中国科学技术大学管理学院,安徽合肥 230026）

考虑分时电价的多目标批调度问题蚁群算法求解

李小林1,张 松2,陈华平2

（1.中国矿业大学矿业工程学院,江苏徐州 221116；2.中国科学技术大学管理学院,安徽合肥 230026）

对同时优化电力成本和制造跨度的多目标批处理机调度问题进行了研究,设计了两种多目标蚁群算法,基于工件序的多目标蚁群算法（J-PACO,Job-based Pareto Ant Colony Optimization）和基于成批的多目标蚁群算法（B-PACO,Batch-based Pareto Ant Colony Optimization）对问题进行求解分析。由于分时电价中电价是时间的函数,因而在传统批调度进行批排序的基础上,需要进一步确定批加工时间点以测定电力成本。提出的两种蚁群算法分别将工件和批与时间线相结合进行调度对此类问题进行求解。通过仿真实验将两种算法对问题的求解进行了比较,仿真实验表明B-PACO算法通过结合FFLPT（First Fit Longest Processing Time）启发式算法先将工件成批再生成最终方案,提高了算法搜索效率,并且在衡量算法搜索非支配解数量的Q指标和衡量非支配集与Pareto边界接近程度的HV指标上,均优于J-PACO算法。

多目标；调度；蚁群算法；批处理机；分时电价

1 引言

批调度问题是调度领域一个重要的研究部分,在现实生产制造环境中有着广泛的应用。如集成电路制造、钢铁生产、货物运输等生产加工过程中[1］,均存在将多个工件作为一批同时进行加工处理的情况。典型的如半导体制造系统中芯片的老化程序,这一过程会将多个工件作为一批同时放在一台测试箱中进行高温预烧,以检验出有潜在缺陷的芯片。此过程中,测试箱即为批处理机器,由于芯片预烧时间必须大于等于预设值,所以一批芯片的加工时间等于所有芯片加工时间的最大值。由于此过程相对其它操作耗时较长（120h相比4-5h）,这使得批处理机的加工成为一个瓶颈环节,对该过程进行优化将有很大的生产意义。

同时,随着“绿色制造”概念的提出,在生产加工过程中考虑能源效率变得愈加重要,通过再造工艺流程、优化生产计划以提高设备利用率、降低能源消耗等也成为研究的重要内容。电能是工业生产中广泛应用的能源,当前很多地区工业用电采用分时电价（TOU,Time of Use）,这让生产过程中合理转移用电负荷、削峰填谷以提高效益、降低能耗提供了可能。

结合分时电价,将批调度过程进行优化,制定合理的分批加工方案,将有效提高生产的经济效益,这也是本文关注的主要内容。

不同于经典调度问题,批调度问题的一个显著特征就是批处理机可以将多个工件作为一批同时进行加工。批调度问题首先由Ikura等[2］提出,其所研究的问题中,工件具有相同尺寸,批容量由其所能容纳的工件个数确定。Uzsoy[3］将问题扩展到工件尺寸不同的情况,对单机情况下最小化Cmax和∑Ci目标函数进行了研究,结合装箱问题证明二者均为NP难的,给出了包含性能较好的FFLPT（First Fit Longest Processing Time）在内的若干启发式算法。在最小化Cmax为目标函数情况下,Dupont等[4-5］提出SKP（Successive Knapsack Problem）和BFLPT（Best Fit Longest Processing Time）两个启发式算法,两者在单机情况下对最小化制造跨度的求解效果优于Uzsoy提出的FFLPT启发式算法。

启发式算法具有实现简单、求解速度快等优点,可以在合理时间内给出可行解,但启发式算法属于贪婪算法,无法预计解的质量。也有研究者使用最优化算法对问题进行求解。Brucker[6］等对以∑wiUi为目标的批调度问题进行了研究,当所有工件具有相同权重时,给出了一个时间复杂度为O（n3）的动态规划算法。Uzsoy等[7］提出了一个分支定界算法求解以最小化总加权完工时间为目标的单机差异工件批调度问题。Dupont等[5］结合FFLPT和BFLPT对最小化制造跨度的单机批调度问题提出一个分支定界算法,取得较好效果。

但由于本文所研究问题是NP难的,最优化的求解方法对大规模的算例求解时会导致难以接受的计算量。Melouk等[8］首先使用元启发式算法对批调度问题进行求解,将所提的模拟退火算法与商业软件CPLEX求解情况做了比较,取得更优的效果。之后又有研究分别采用遗传算法[9-10］、蚁群算法[11-12］和微粒群算法[13］等对该类问题进行了求解和比较,结果均显示元启发式算法在不同规模算例下,均可以在合理时间内稳定的取得较高质量的解。

以上研究在目标函数上均为单目标,在多目标单机批调度问题方面尚没有进行广泛的研究。已有研究中,Kashan等[14］给出两种混合多目标遗传算法BHMOGA和SMOGA对最小化制造跨度和最小化最大延迟这两个目标进行优化,结果显示BHMOGA优于SMOGA。

本文在最小化制造跨度的同时,将能源消耗作为优化目标之一对批调度问题进行求解。将工件加工时间和分时电价结合起来计算的电力成本,作为能源消耗这一目标的计算依据。由于分时电价是时间的函数,具有周期性波动的特点,在确定批加工顺序之后需要进一步得到各批开始加工时间才能对电力成本进行计算。因此,在对问题进行求解时,提出按时间点进行工件和批分配的两种蚂蚁算法对此类多目标问题进行求解。

对于批调度及多目标调度更全面的文献回顾可参见Potts[15］和Lei Deming[16］。

2 问题模型

本文在研究目标上考虑制造跨度和电力成本,是典型的多目标组合优化（MOCO,Multiple-Objective Combinatorial Optimization）问题[17］。一般化的MOCO问题可以描述如下：

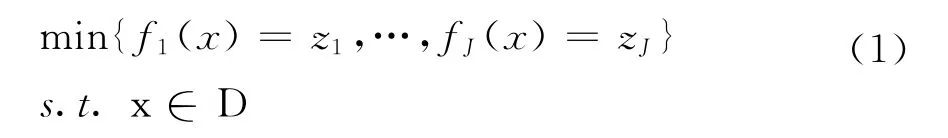
x=[x1,…,xN］为N维离散型决策变量, fi（x）为第i个目标函数,D是可行解集。

如果∀i∈｛1,…,J｝,有fi（x′）≥fi（x）,并且至少在一个目标i上满足fi（x′）＞fi（x）,则称解x支配（dominate）解x′。

在多目标优化算法中,针对其当前在搜索过程中找到的最优个体（即当前最优解）,我们算法搜索到的当前最优解称之为非支配解（Non-Dominated solution）,所有非支配解的集合,称作当前群体的非支配集（Non-Dominated Solutions,NDS）。

如果不存在x′∈D支配解x*,则称解x*为Pareto最优解,所有的Pareto最优解的集合称为Pareto最优解集或Pareto前沿。

本文所研究问题可具体描述如下：

（1）n个工件的集合J=｛1,2,…,n｝,工件i的加工时间为pi,尺寸为si。

（2）机器容量为C,单个工件尺寸si均小于机器容量,每个批中工件尺寸之和不超过机器容量。

（3）同一批工件具有相同的开始、结束加工时间,从一批开始加工直到该批加工完成,整个过程不允许中断,批b的加工时间Pb由该批中加工时间最大的工件决定。所有机器和工件均在0时刻可用。任一批b开始加工时间为Sb,则其完工时间Cb= Sb+Pb。

（4）两个最优化目标分别为最大制造跨度Cmax和电力成本EC。Cmax为最后一批工件的完工时间。用电价函数为f（t）来表示任意时刻t的电价。机器功率恒定记为1,用电价乘以一批工件加工时间来表示该批工件加工的电力成本。总的电力成本EC即为所有批加工的电力成本之和。

（5）一个解方案中所有批的集合用B表示,批可以在任意一个时刻开始加工,但每个时刻最多有一个批在加工。

所研究问题以三参数表示法可表示为1| batch,pi,si≤C|｛Cmax,EC｝其中,batch表示机器为批处理机。pi和si表示工件具有不同加工时间及尺寸。基于上面的假设及符号说明,可建立问题相应数学模型如下：

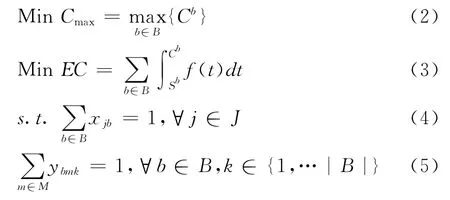
其中：式（2）和式（3）为优化的目标函数制造跨度Cmax和总电力成本EC。式（4）表示一个工件必须且只能属于一个批。式（5）要求一个批只由一台机器在第k位置加工。式（6）表明机器容量约束,一批中所有工件之和应小于等于机器容量。式（7）指批的加工时间由批中加工时间最长的工件决定。式（8）计算任一批的完工时间。式（9）表明,前一批加工完成后,后一个批才能开始加工。式（10）和式（11）约束决策变量只能取0或1。

3 两种蚁群算法

根据信息存储和解的编码的不同,本文给出两种多目标蚁群算法对所研究的多目标批调度问题进行求解,本文考虑的两个目标一个衡量加工时间,另一个衡量在分时电价条件下的电力成本。显然,在单机情况下,各工件开始加工时间不同,会导致不同的最大完工时间,又由于不同时段电价不同,所以,各工件在不同时间点开始加工同样会影响电力成本。当工件序列成批方案确定后,在极端情况下,当所有批连续加工时,可得到最小的最大完工时间,而当所有批避开高电价时段,均在低电价时段加工时,则可得到最小的电力成本,但此时显然会增大最大完工时间。

两种蚁群算法通过将工件序列调整为在不同时间点加工的批来获得最终的解,从而需要先确定将所有工件加工完成所需要的最大时间长度。下面,通过定义所研究问题Cmax目标的上下界,给出将所有工件加工完成需要的时间点数。

定义1 将所有工件加工完成的制造跨度为t,对应电力成本为ECt,如果不存在t+Δt,Δt＞0,使得ECt+Δt＜ECt,则称t为制造跨度上界C。

步骤1将工件集合J中所有工件按加工时间非增序排列；

步骤2每个工件单独成一批,得批序列B；

步骤3从批序列B头部选择一个批b,将其安排在第一个未占用低电价时段开始时间点加工。重复步骤3直至所有批安排加工完成,所得最大完工时间即为制造跨度上界。

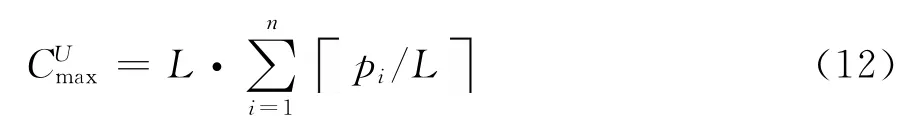
步骤1 将工件集合J中每个工件松弛为si个加工时间为pi的单位尺寸工件,得到工件集合Ju；

步骤2 将工件集合Ju中的工件按加工时间非增序排列；

步骤3 依次将Ju中iC+1～（i+1）C个工件分为一批,其中i=0,1,…,|Ju|/C,x表示小于等于x的最大整数,得批集合B；

步骤4 批集合B中所有批加工时间之和即为制造跨度下界。

用一个时间点表示一个单位的时间,显然将所有工件加工完成所需要的时间点数N,满足C≤N≤C。

在电力成本方面给出如下两个定义,以用于之后对算法的性能分析。

3.1 多目标蚁群算法流程

（1）基于工件序的多目标蚁群算法

基于工件序的多目标蚁群算法（J-PACO,Jobbased Pareto Ant Colony Optimization）构造解的方式为,先将工件安排至时间线的各时间点,再将各时间点上的工件作为一批进行加工。当所有工件成批完成后,即可以确定方案的Cmax及EC,继而根据两个目标函数值分别对各目标的信息素进行更新,循环直至结束条件满足,完成算法对解的搜索。

J-PACO算法对问题求解流程如下：

（2）基于成批的多目标蚁群算法

对于工件尺寸不同的单机批调度问题,Uzsoy[3］结合装箱问题中的FF（First Fit）算法[28］给出了以最小化Makespan为目标,求解批调度问题的BFF（Batch First Fit）算法,并根据初始时工件排序不同给出若干种启发式算法。其实验表明,当初始时工件按加工时间降序排列,再使用BFF算法将工件成批得到的FFLPT（First Fit Longest Processing Time）算法对问题的求解效果优于其它算法。FFLPT算法对单机批调度问题求解流程如下：

FFLPT算法流程：

步骤1 将工件按加工时间降序排列；

步骤2 依次选择工件序列中的工件,并将之放在第一个可以容纳该工件的批中,如果没有批可以容纳该工件,则将该工件放入新批中。重复步骤2直到所有工件分批完成。

基于成批的多目标蚁群算法（B-PACO,Batchbased Pareto Ant Colony Optimization）构造解的方式为,蚁群算法将工件序按FFLPT算法成批,再将批分到时间线进行加工。所有批加工完成后,即完成整个方案的调度。根据Cmax和EC两个目标函数值,对解元素的信息素进行更新,循环算法至终止条件满足,完成解的搜索。

B-PACO算法对问题求解流程如下：

3.2 信息素

多目标蚁群算法中,可将信息保存在一个信息素矩阵中,也可为每个目标设置各自的信息素矩阵。为了使信息素对不同的目标具有区分性,本文采用后者,即对于每个目标k,将信息素保存在不同的信息素矩阵中。当蚁群算法对解的构造方式不同时,信息素的含义也不同。

在算法J-PACO中,算法在每个时间点选择合适的工件进行加工,因而,信息素保存在工件和时间点之间。使用τCmax（i,t）表示在Cmax目标的信息矩

阵中,工件i和时间点t之间的信息素,使用τEC（i, t）表示在EC目标的信息矩阵中,工件i和时间点t之间的信息素。初始信息素为τ0。

而在B-PACO算法中,由于工件序列先通过FFLPT成批,蚁群算法主要将批分配到不同时间点,因而,信息素保存在批与时间点之间。使用τCmax（b,t）表示在Cmax目标的信息矩阵中,批b和时间点t之间的信息素,使用τEC（b,t）表示在EC目标的信息矩阵中,批b和时间点t之间的信息素。

3.3 启发式信息

启发式信息表示蚂蚁在构建解时,选择下一个工件的期望程度,好的启发式信息可以增加蚂蚁找到近优解的速度。

（1）算法J-PACO中启发式信息

在J-PACO算法中,由于将工件分到时间线上后,按时间点对工件成批,即算法将工件成批和将批分配到机器作为一个整体进行处理,所以只需考虑将一个时间点的工件作为一个批进行构造的启发式信息。蚂蚁确定当前未安排工件i,并将之安排在可用时间点集合中合适的时间点来完成解的构造。显然,从工件加工时间考虑,应使一个批中工件加工时间尽量接近,加大批的负载均衡。从工件尺寸考虑,应使批的剩余空间最小,以提高批的利用率。根据这些考虑,给出如下的启发式信息。

（2）算法B-PACO中启发式信息

B-PACO算法对解的构造,主要是将批分配到各时间点,为了降低电力成本,算法应尽量将批安排到低电价时段进行加工。又由于批加工过程不可中断,因而算法在构造解时,应将批分配到剩余时长与批加工时间相近的时间点进行加工。给出如下的启发式信息。

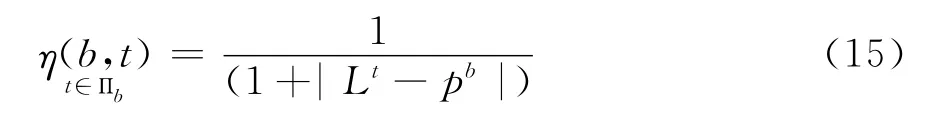
其中,Πb,表示对当前批而言,可安排的时间点集合。Lt表示时间点t所处的电价时段未安排加工的时间长度。

3.4 状态转移概率

蚁群算法构建解的过程就是将工件（J-PACO算法中）或批（B-PACO算法中）安排在各时间点的过程,当所有工件或批安排完成后,即完成了解的构建。本文中设计的两种蚁群算法均是顺次将未安排的工件或批安排在合适时间点上的过程。

在J-PACO算法中,当前可用时间点的确定应满足两个条件a）时间点未被前一批加工所占用；b）当前时间点已经安排工件加工尺寸之和不超过机器容量。而B-PACO算法中,由于成批已经完成,所以,只需要满足条件a）即可。

（1）J-PACO算法中状态转移概率

J-PACO算法中,蚂蚁首先确定当前未安排工件i,继而按式（16）在可用时间点集合Πi中选择时间点t来安排工件i。

其中,q为[0,1）区间产生的随机数,参数q0（0≤q0＜1）事先确定。显然,q0越大,则蚂蚁越易选择当前最优时间点,算法倾向于收敛,q0越小,则算法倾向于按概率选择最优时间点,增加算法对解空间探索能力。参数α和β用来区别信息素和启发式信息的相对重要程度。

（2）B-PACO算法中状态转移概率

与J-PACO算法类似,只需将工件换作批,从可用时间点集合Πb按式（18）选择时间点t进行加工即可。

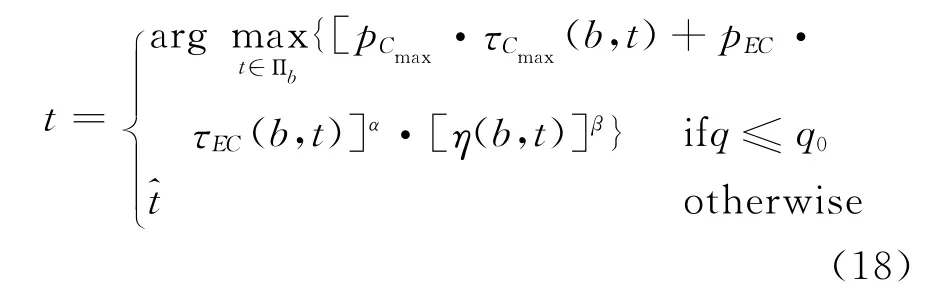
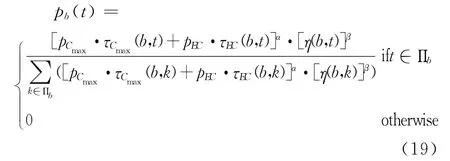
3.5 信息素更新

当所有工件分到时间线上,并成批完成后,即得到一个完整的调度方案,当方案构造完成后,为了增加优秀方案中解元素的信息素浓度,降低劣解元素的信息素浓度来指导蚂蚁的下一步向近优解的搜索。需要对解元素进行信息更新,信息素更新主要包括信息素挥发和信息素释放两部分,记当前迭代中所有蚂蚁在目标k上得到的迭代最优解为,搜索得到的全局最优解为。

J-PACO算法中对各个目标k的信息素更新按式（20）进行。

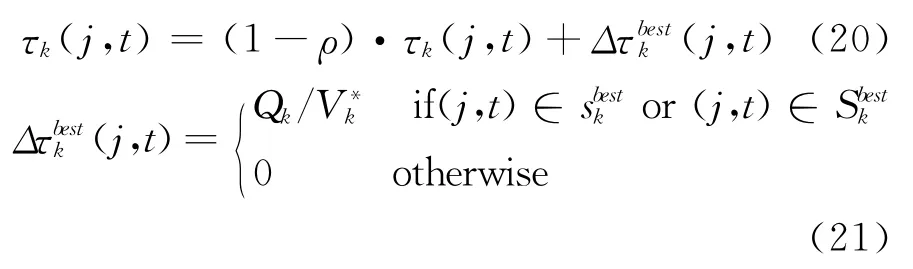
将工件换作批,在B-PACO算法中,对各个目标k的信息素更新按式（22）进行。

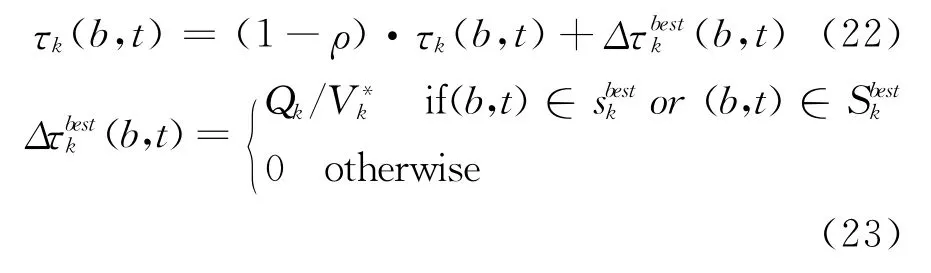
4 仿真实验与分析

4.1 实验设计

本文通过随机生成算例,对所提算法的有效性进行比较。算例的生成,主要考虑工件数量、工件加工时间、工件尺寸、电价时段个数、各电价时段长度、各电价时段价格。简化起见,本文中,考虑电价时段个数为2,即只分为高电价时段和低电价时段,各电价时段时长相同,且高电价时段电价为低电价时段电价2倍。批处理机容量为10。实验中,使用JiPiLk（i=1,2,3；i=1,2；k=1,2）来表示各类实例。各因素的具体取值如表1所示。

表1 算例生成的分类因素及取值

不同于单目标问题,多目标问题中对解质量的衡量不仅涉及解本身数值的好坏,还要考虑所求Pareto解解的数量以及在解空间的分布情况。为了衡量各算法对所研究多目标问题的求解性能,实验中采用数量指标Q和超体积指标（Hypervolume Indicator）[19］对算法求解结果进行比较。

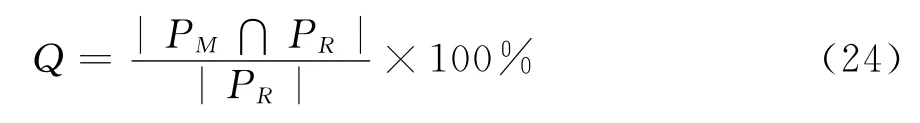
其中,PM表示算法M得到的非支配解集,PR表示所有算法得到的非支配解集。|X|表示集合X中元素个数。显然,Q∈[0,1］,该值越大,说明相应算法可以找到更多的非支配解。

超体积指标（Hypervolume Indicator）是衡量一个非支配集与Pareto边界接近程度的指标[19］,该值通过比较不同算法得到的Pareto解集相对于参考点形成的超体积大小来衡量解的质量。本文设置参考点W=（CUmax,ECU）,用各算法所求非支配解与参考点W所形成的超体积比率,来比较算法之间求解效果[14］。

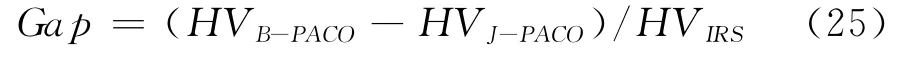
其中,HVX表示算法X所得非支配解相对于参考点W的超体积。取IRS=（CLBmax,ECLB）为理想参考集,则HVIRS表示理想参考集的超体积。Gap值为正时,表示B-PACO算法性能优于J-PACO算法。我们使用HVX/IRS来表示X算法的HV值与理想参考集HV值的比率,即HVX/IRS= HVX/HVIRS×100%,此值越大,则表明算法取得更优的非支配解集。

4.2 参数设置

通过初步实验,对算法J-PACO和B-PACO的参数按表2设置时对问题具有理想的求解效果。将蚁群算法种群规模增大时,算法可找到更优的非支配解集,但运算时间会大幅增加,在本文所测试算例的规模下,综合考虑解的质量和运算时间,将种群规模设置为30。在接下来的实验中,将两个算法运行相同的迭代次数,已使结果更有可比性。

所有算法使用Visual C#语言实现,运行环境为Intel E2200处理器,2GB内存。

4.3 实验结果与分析

表3给出了各算法对问题的求解结果比较,表中第一列为算例分类,第三到五列为J-PACO算法的Q值、HV/IRS值和运行时间数据。第六到八列为B-PACO算法的Q值、HV/IRS值和运行时间数据。最后一列为B-PACO算法相对于J-PACO算法的Gap值。

从Q值可看出,在算法找到的非支配解数目上,B-PACO具有绝对优势,并且随着工作数目的增加,算法B-PACO的Q值优于J-PACO的趋势增加,这说明当问题规模增加时,B-PACO算法更有可能找到更多的非支配解。

表2 算法参数设置

表3 各算法求解结果比较

从HV/IRS值看,随着问题规模的增加,二种算法HV/IRS值均变小,这主要是因为,当问题规模增加时,在本文计算方式下,时间线长度会增加很快,从而导致HVIRS的值迅速增加。但B-PACO算法的HV/IRS值始终大于J-PACO算法的HV/ IRS值,这表明,B-PACO算法在所找到非支配解集的质量上要优于J-PACO算法。从Gap值可看出,两种算法的HV/IRS值差距在缩小,这表明JPACO在解的构造上有优势,这主要是因为,JPACO算法在构造解时由于考虑的是将工件分配到时间点,从而在成批的多样性方面要优于B-PACO算法仅使用FFLPT成批,即J-PACO对于解的多样性搜索能力要优于B-PACO算法。

完成相同的迭代次数,J-PACO算法在运行时间上,要远大于B-PACO算法,这也是因为二者对解的构造方式不同导致。B-PACO算法首先将工件成批,再将批分配到时间线上,这相对于J-PACO直接将工件成批和批分配到时间线结合在一起的方式而言,显然大大缩小了蚁群算法中解元素的数目,从而提高了速度。B-PACO算法对算例求解时间包括将工件成批以及将批分配到时间线两个阶段,但由于将工件成批时使用FFLPT启发式算法完成,这也大大节约了算法的求解时间。另外,加工时间和电价时段长度均会影响时间线长度继而影响蚁群算法解元素个数,从表3中可看出,加工时间和电价时段长度增加时,各算法运行时间均增加。

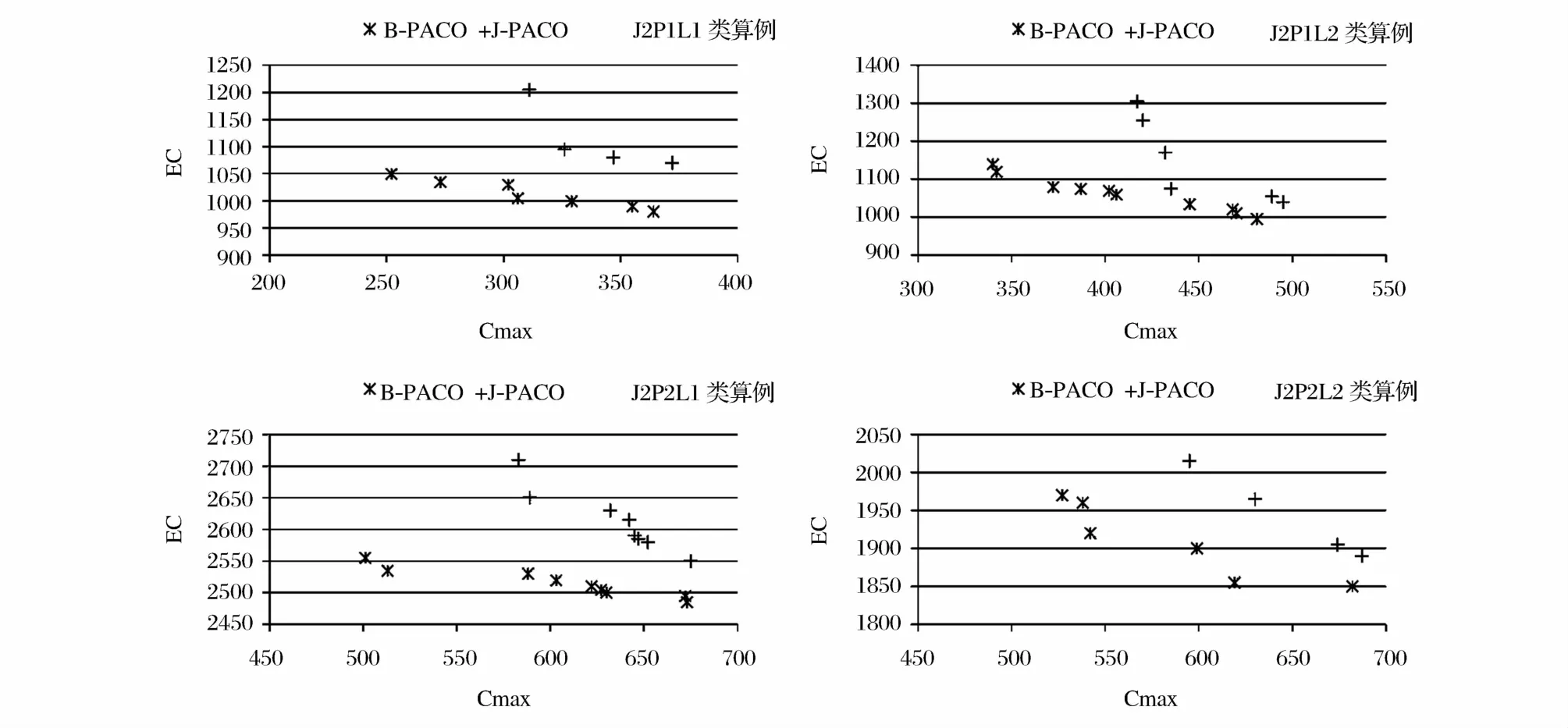
图1 各算法求解J2类算例所得非支配解集

图1显示了算例规模为50时,J-PACO算法和B-PACO算法所解得非支配解集对比情况。由图中易看出,B-PACO算法求解结果普遍优于J-PACO算法,从所搜索的非支配解数目上,B-PACO算法基本优于J-PACO算法的搜索结果。由于问题优化的两个目标均为最小化目标,而B-PACO算法在各个解目标上均优于J-PACO求解效果,所以B-PACO算法所得非支配解集基本分布在J-PACO所得非支配解集的左下方。这里也可以直观的看出前面所定义超体积指标真实的反映了算法对问题的求解效果。从图1的各子图中还可观察到B-PACO的解向Cmax较小方向上分布,这主要是因为J-PACO算法将工件在整个时间线上分布并构造批,而BPACO先使用启发式算法成批,批的利用率较高,从而易于找到Cmax较小的解。

5 结语

本文将批处理机调度问题扩展到多目标范围,在单机环境下,将工件制造跨度以及方案所需电力成本同时进行优化。设计两种蚁群算法J-PACO和B-PACO对此多目标组合优化问题进行了求解,JPACO将工件成批和分配到时间点进行加工作为一个整体进行了考虑,具有较高的算法复杂度,而BPACO算法先使用FFLPT启发式算法将工件成批,之后着重考虑将批分配到不同时间点进行加工,相比之下降低了问题复杂度,提高了批的利用率。通过之后的实验也可看出,B-PACO算法在搜索到非支配解的数量和质量上均优于J-PACO算法。

从实验中也可看出,由于算法设计机制原因,JPACO算法在具有较高复杂度的同时,可以对解的多样性进行更有效的搜索。下一步可以设计更为有效的算法对问题进行求解,同时也可对机器环境等进行扩展,以应用到调度领域的其它问题。

[1］Ahmadi J H,Ahmadi R H,Dasu S,et al.Batching and scheduling jobs on batch and discrete processors[J］. Operations Research,1992,40（4）：750-763.

[2］Ikura Y,Gimple M.Efficient scheduling algorithms for a single batch processing machine[J］.Operations Research Letters,1986,5（2）：61-65.

[3］Uzsoy R.Scheduling a single batch processing machine with nonidentical job sizes[J］.International Journal of Production Research,1994,32（7）：1615-1635.

[4］Dupont L,Ghazvini F J.Minimizing makespan on a single batch processing machine with non-identical job sizes [J］.APII-JESA Journal Europeen des Systemes Automatises,1998,32（4）：431-440.

[5］Dupont L,Dhaenens-Flipo C.Minimizing the makespan on a batch machine with non-identical job sizes：An exact procedure[J］.Computers&Operations Research, 2002,29（7）：807-819.

[6］Brucker P,Kovalyov M Y.Single machine batch scheduling to minimize the weighted number of late jobs[J］. ZOR-Mathematical Methods of Operations Research, 1996,43（1）：1-88.

[7］Uzsoy R,Yang Yaoyu.Minimizing total weighted completion time on a single batch processing machine[J］.Production and Operations Management,1997,6（1）：57-73.

[8］Melouk S,Damodaran P,Chang Pingyu.Minimizing makespan for single machine batch processing with nonidentical job sizes using simulated annealing[J］.International Journal of Production Economics,2004,87（2）：141-147.

[9］Damodaran P,Manjeshwar P K,Srihari K.Minimizing makespan on a batch-processing machine with non-identical job sizes using genetic algorithms[J］.International Journal of Production Economics,2006,103（2）：882-891.

[10］Kashanl A H,Karimi B,Jolai F.Minimizing makespan on a single batch processing machine with non-identical job sizes：A hybrid genetic approach[M］.∥Raidl J G G R.Evolutionary Computation in Combinatorial Optimization.Springer-Verlag Berlin：Berlin, 2006：135-146.

[11］王栓狮,陈华平,程八一,等.一种差异工件单机批调度问题的蚁群优化算法[J］.管理科学学报,2009,12（6）：72-82.

[12］杜冰,陈华平,程八一,等.具有不同到达时间的差异工件批调度问题的蚁群聚类算法[J］.系统工程理论与实践,201030（9）：1701-1709.

[13］程八一,陈华平,王栓狮,基于微粒群算法的单机不同尺寸工件批调度问题求解[J］.中国管理科学, 2008,16（3）：84-88.

[14］Kashan A H,Karimi B,Jolai F.An effective hybrid multi-objective genetic algorithm for bi-criteria scheduling on a single batch processing machine with non-identical job sizes[J］.Engineering Applications of Artificial Intelligence,2010,23（6）：911-922.

[15］Potts C N,Kovalyov M Y.Scheduling with batching：A review[J］.European Journal of Operational Research,2000,120（2）：228-249.

[16］Lei Deming.Multi-objective production scheduling：a survey[J］.International Journal of Advanced Manufacturing Technology,2009,43（9-10）：926-938.

[17］Jaszkiewicz A.Genetic local search for multi-objective combinatorial optimization[J］.European Journal of Operational Research,2002,137（1）：50-71.

[18］Johnson D S,Demers A,Ullman J D,et al.Worst-case performance bounds for simple one-dimensional packing algorithms[J］.SIAM Journal on Computing,1974,3（4）：299-325.

[19］Zitzler E,Thiele L.Multiobjective optimization using evolutionary algorithms-A comparative case study [M］//E：ben A E.Parallel problem solving from nature-Ppsn V.Berlin：Springer-Verlag Berlin,1998：292 -301.

Solving Multi-objective Batch Scheduling Under TOU Price Using Ant Colony Optimization

LI Xiao-lin1,ZHANG Song2,CHEN Hua-ping2

（1.School of Mines,China University of Mining and Technology,Xuzhou 221116,China；2.School of Management,University of Science and Technology of China,Hefei 230026,China）

The problem of scheduling batch processing machines is considered in this study.Batch processing machines are encountered in various manufacturing environment and the study is motivated by burningin operation in semiconductor manufacturing while time-of-use electricity price is considered as well.In the problem under study,jobs seizes are non-identical and machines are batch processing machines which can process several jobs simultaneously as a batch.Since the electricity price is time related,the objectives of electrical cost and makespan is influenced by start processing time of each batch.These two objectives were minimized simultaneously on single batch processing machine with non-identical job sizes.Two pareto ant colony optimization algorithms were designed to solve the problem.One is J-PACO（Job-based Pareto Ant Colony Optimization）algorithm and the other is B-PACO（Batch-based Ant Colony Optimization）algorithm.This problem is different from traditional batch scheduling problems.As the price is related to the time,the start processing time of jobs should be determined after the sequence of batches are fixed.In the two algorithms proposed,jobs and batches are scheduled on time line separately.Random job instances are generated in the simulation experimentation to evaluate the performance of algorithms proposed.The experiment results indicate that B-PACO,which group jobs into batches using FFLPT（First Fit Longest Processing Time）,outperforms J-PACO in computational time,numbers of non-dominated solution and hypervolume.The study will be helpful in the application of ACO involving multi objectives.And,the idea of allocating jobs in a time line before they are grouped into batches can also be used in scheduling batch processing machines.

multi-objective；scheduling；ant colony optimization；batch processing machine；TOU price

TP301

A

1003-207（2014）12-0056-09

2012-03-19；

2013-05-14

创新研究群体科学基金资助项目（70821001）；国家自然基金资助项目（71171184）；中国矿业大学青年科技基金项目（2014QNA48）；国家自然科学青年基金项目（71401164）

李小林（1986-）,男（汉族）,江苏徐州人,中国矿业大学矿业工程学院,讲师,研究方向：智能优化算法、信息系统.