基于孔隙介质模型的散体材料桩复合地基沉降分层总和分析方法*

曹文贵，唐旖旎，王江营

(湖南大学 岩土工程研究所，湖南 长沙 410082)

散体材料桩(如碎石桩、砂石桩等)加固软土地基或路基是一种广泛应用的地基加固处理技术，且散体材料桩复合地基沉降分析是地基加固处理与基础工程设计的重要依据．但是，由于这种地基的明显不均匀性和应力-应变关系复杂性，使得其沉降分析理论及方法研究还需要深化和完善，有必要对此进行更深入地研究.

目前，复合模量法[1-3]是最为广泛的复合地基沉降分析方法之一，其基本思路是采用桩土复合模量代替天然地基压缩模量，再以分层总和法来计算复合地基的沉降，为此，盛崇文[1]利用桩土复合地基的面积置换率，将载荷试验确定的桩土模量进行简单的加权平均处理以获得复合模量；Omine[2]建立了双重介质模型，在考虑桩与土各向异性基础上，利用桩土复合地基面积置换率来确定复合模量，王凤池等[3]考虑了桩长、桩端土性质对复合模量的影响，并利用复合地基桩体承载机理来修正复合模量面积比公式，从而对复合模量进行修正.另外，张定[4]基于碎石桩复合地基变形是竖向变形和横向变形的叠加，提出了一种桩土复合地基沉降分析方法.虽然上述各种方法获得了一定的成果，但是，均未体现附加应力和应力历史对复合地基变形力学参数的影响，而且，须采用压缩试验曲线或静载试验曲线来描述桩土模量的变化，这给实际工程计算带来了不便.于是，曹文贵和刘海涛等[5]基于桩土复合地基沉降变形机理及其非线性特征，考虑荷载作用下桩土变形力学参数的变化，建立了刚性基础下散体材料桩复合地基沉降计算新方法.该方法反映了桩土变形力学参数的变化对复合地基沉降的影响，并且在沉降分析中避免了使用压缩试验曲线或静载试验曲线来描述模量的变化，使沉降计算过程更公式化.但是，这种方法并未反映桩土泊松比变化对复合地基沉降分析的影响，而且，在研究桩土模量变化规律时忽略了高阶变形微量的影响，存在明显的缺陷.如果在此方法的基础上合理地解决桩土模量和泊松比变化对沉降分析的影响，必将获得更为合理的散体材料桩复合地基沉降计算方法，这正是本文研究的核心内容.

为此，本文将考虑散体材料桩复合地基桩与土的孔隙特点，从其变形微观力学机理研究入手，采用孔隙介质力学理论，通过分别研究桩与土变形力学参数(包括模量和泊松比)的变化规律，来探讨散体材料桩复合地基沉降分析新方法，以期完善散体材料桩复合地基沉降分析的理论方法.

1 散体材料桩复合地基沉降分析模型

为了建立散体材料桩复合地基沉降分析模型，首先做如下假定：

1)建筑结构基础为理想刚性基础，因此，桩与土的竖向变形是协调相等的.

2)桩与土界面水平或侧向变形连续.

3)考虑到散体材料桩具有较强的透水性，孔隙水极易排出，因此，不考虑孔隙水压力对地基沉降的影响.

因此，为了分析复合地基沉降，只需求出土体的沉降量.于是，基于文献[5]的研究思路，将散体材料桩复合地基压缩层分为M1层，设第i压缩分层产生的竖向变形为Si，于是，总沉降S可视为各压缩分层竖向变形量之和，即：

(1)

将第i压缩分层所受附加应力分为M2i级，则该层土体竖向变形Si可视为各级附加应力作用产生的竖向变形量的总和，即：

(2)

式中：dsi为第i压缩分层厚度；εszij为第i压缩分层在第j级荷载作用下产生的竖向应变.于是，式(1)亦可改写为：

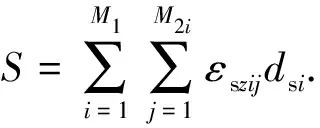
(3)

2 桩或土体孔隙介质力学模型

散体材料桩复合地基的桩和土均为孔隙介质体,在荷载作用下，其中孔隙可以被压缩，即桩或土的体积会发生变化，从而，导致其变形力学参数也会随之而变化，但是，散体材料桩和土颗粒骨架可视为传统固体力学研究对象，其变形力学参数为常数[6]，因此，从孔隙介质微观分析入手，就有可能建立孔隙介质变形力学参数与孔隙介质骨架变形力学参数之间的关系.为此，必须探讨孔隙介质体应力与变形分别与颗粒骨架的应力和变形的关系，前者称为孔隙介质的表观应力和表观变形(文献[6]中称为视应力和视应变)，后者称为孔隙介质骨架的实际应力和实际变形，然后据此可建立孔隙介质力学模型，详细内容如下.

设孔隙介质体(包括桩体与土体)的视应力为σ，孔隙率为n，其颗粒骨架实际应力为σs，由文献[6]可得它们之间的关系为：

(4)

Lsx=(1-n)Lx，

(5)

(6)

如果令：

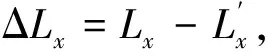
(7)

(8)

Δn=n-n′．

(9)

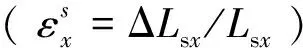
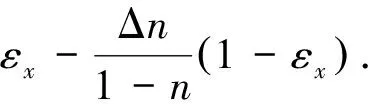
(10)

(11)

(12)

Vs=(1-n)V，

(13)

(14)

如果令：

ΔV=V-V′，

(15)

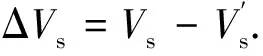
(16)

(17)

式(17)亦可改写为：

(18)

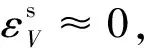
Δn=εV(1-n)/(1-εV)．

(19)

将其代入式(10)～(12)可得：

(20)

(21)

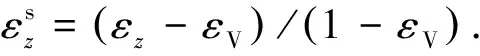
(22)

同时，根据弹性力学理论[7]，孔隙介质表观体应变εV可按式(23)进行计算：

(23)

忽略其中的三阶微量，则式(23)亦可改写为：

(24)

上述即为散体材料桩复合地基孔隙介质力学分析模型，下面将在此基础上探讨桩或土体变形力学参数变化规律.

3 桩与土变形力学参数变化规律

3.1 附加应力作用下桩和土变形力学参数变化规律

1)桩和土泊松比的变化规律

μsij=-εsxij/εszij或μsij=-εsyij/εszij,

(25)

(26)

将式(20)～(22)代入式(26)得：

(27)

再将式(24)及(25)代入式(27)并结合式(26)可得出μsij与νsij之间的关系，即：

(28)

其与文献[6]结果存在较大差别，文献[6]认为土体与其颗粒骨架泊松比是相同的即νsij=μsij，显然不合理，因为它没有反映土体变形力学参数随土体变形而变化的特点，而本文得到的相应关系正反映了变形对土体泊松比的影响，因此，本文得到的相应关系更具合理性.

仿照上述推导过程，可得到在第j-1级附加应力增量的作用下该层土体视泊松比μsi(j-1)与土颗粒骨架实际泊松比νsi(j-1)之间的关系，即：

νsi(j-1)=

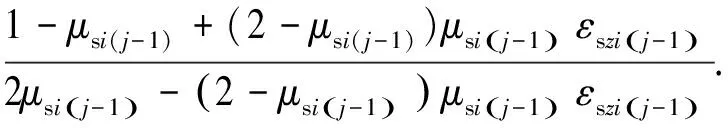
(29)

由于在第j级附加应力增量作用下该层土体变形分析中采用递推方法，故式(29)右端各参量均为已知，于是，νsi(j-1)为已知，另外，认为颗粒骨架变形力学参数不变即νsij=νsi(j-1)，则利用式(28)可得：

(30)

式(30)可转化为关于μsij的一元二次方程，求解该方程并取其合理解可得：

(31)

式中νsi(j-1)采用式(29)计算.式(31)即为附加应力增量作用下第i压缩分层土体视泊松比变化规律，其为一个递推公式，因此，必须用到第i压缩分层土体在附加应力作用之前的初始泊松比μsi0，这将在本文3.2节讨论.

仿照土体视泊松比变化规律的研究过程，设第i压缩分层桩体在第j级附加应力增量作用下产生的竖向和水平向应力增量为σPzij和σPxij，σPyij，相应视应变分别为εPzij和εPxij，εPyij，可推得相应桩体视泊松比μPij的变化规律，即：

μPij=

(32)

其中νPi(j-1)为在第j-1级附加应力增量作用下该层桩体散体材料骨架颗粒实际泊松比，可按式(33)计算：

(33)

式(32)同样为一个递推计算公式，递推计算过程需要的第i压缩分层桩体在附加应力作用之前的桩体视泊松比μPi0，同样将在本文3.2节讨论.

2)桩或土视模量的变化规律

仿照前述方法，首先对第i地基压缩分层土体在第j级竖向附加应力增量作用下进行分析，那么采用增量虎克定律描述其应力应变关系为[7]：

(34)

(35)

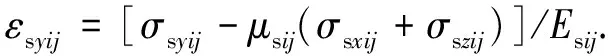
(36)

式中：Esij和μsij分别为第i压缩分层土体在第j级竖向附加应力增量作用过程中变形模量和泊松比的平均值.针对土颗粒骨架采用增量虎克定律[7]得：

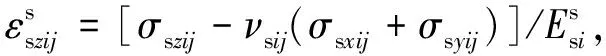
(37)

(38)

(39)

(40)

(41)

(42)

利用式(34)～(42)可得式(43)：

(43)

将式(22)，(25)及(26)代入式(43)，则式(43)可改写为：

(44)

由于假设土颗粒骨架变形模量为常数，可利用式(44)得到第i地基压缩分层土体在第j-1级附加应力增量作用下的变形模量Esi(j-1)的计算公式，即：

(45)

令式(44)和(45)中等式右端分别用符号αsij与αsi(j-1)代替，结合两式可得：

(46)

式(46)即为在附加应力作用下第i压缩分层土体视变形模量的变化规律.可以看出式(46)同样要采用递推方法计算，且需知道视变形模量在附加应力作用之前的初始值Esi0，这将在本文3.2节讨论.

另外，由式(44)和(45)可知，第i压缩分层土体视变形模量的变化会受到土体孔隙率变化的影响，必须讨论该层土体在附加应力增量作用下孔隙率变化规律.为此，结合式(24)与(25)可得第j级竖向附加应力增量作用下该层土体视体积应变的另一个表达形式，即：

(47)

将式(47)代入式(19)可得土体孔隙率变化量，即：

(48)

将式(48)代入式(9)可得第i压缩分层土体在第j级竖向增量附加应力作用后的孔隙率表达式，即：

nsij=

(49)

式(49)也为一个递推计算公式，须用到第i压缩分层土体在附加应力作用之前的孔隙率nsi0，这将在本文3.2节讨论.

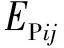
(50)

(51)

式中：nPij为第i压缩分层桩体在第j级竖向附加应力增量作用下的孔隙率.令式(50)及(51)中等号右端项分别用符号αPij和αPi(j-1)代替，可得附加应力作用下第i压缩分层桩体变形模量变化规律，即：

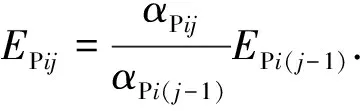
(52)

式(52)同样需采用递推方法进行计算，其初始值EPi0的取值也将在本文3.2节讨论.

附加应力作用下桩体变形模量的变化同样受其孔隙率变化的影响，仿照式(49)方法可得第i压缩分层桩体在第j级竖向附加应力增量作用下孔隙率的变化规律，即：

nPij=nPi(j-1)-

(53)

桩体孔隙率的变化同样需采用递推方法进行计算，其初始值nPi0的取值也将在本文3.2节进一步讨论.

3)桩和土附加应力确定方法

由散体材料桩复合地基沉降分析模型可知，要求得散体材料桩复合地基沉降值，须知道土体所受的应力增量.因为散体材料复合地基中桩与土相互影响，因此，必须从这一力学特点入手，对桩或土体进行受力分析，以求得散体材料桩复合地基的桩土应力比，从而建立散体材料桩复合地基土体所受附加应力的确定方法，具体过程如下.

以土体单元为例探讨桩或土的受力情况.本文参考文献[4,5,8,9]的方法，在第i地基压缩分层取一个土体单元，在第j级附加应力增量作用下，考虑水平向对称的情况，即σsxij=σsyij，并且为了分析方便，将土体单元受力变形分解为只发生水平向应变或竖向应变的两种模型[4,5,8,9]，如图1所示，于是，各模型应力应变关系如下：

σszij=σszija+σszijb，

(54)

σsxij=σsxija+σsxijb，

(55)

εszij=εszija+εszijb，

(56)

εsxij=εsxija+εsxijb．

(57)

图1 土体单元受力分析

利用两种模型分别结合增量虎克定律对土体单元进行分析，根据式(54)，(55)可得土体单元竖向及水平向应力与应变的关系[5]，即：

σszij=Esij[2μsijεsxij+(1-μsij)εszij]/[(1+

μsij)(1-2μsij)]，

(58)

σsxij=Esij(εsxij+μsijεszij)/[(1+μsij)(1-2μsij)]．

(59)

取相应桩体单元进行分析，利用上述方法可得桩体单元竖向及水平向应力与应变关系为[5]：

σPzij=EPij[2μPijεPxij+(1-μPij)εPzij]/[(1+

μPij)(1-2μPij)]

(60)

σPxij=EPij(εPxij+μPijεPzij)/[(1+μPij)(1-

2μPij)]．

(61)

由于散体材料桩复合地基土体所受应力必须考虑桩土相互作用，因此，下面将考虑桩与土所分担应力的不同，讨论土体附加应力的确定方法.设散体材料桩复合地基面积置换率为m，第i压缩分层在第j级附加应力增量作用下桩与土应力比为Nij(即σPzij/σszij)，根据文献[4]可得：

εsxij=[m/(m-1)]εPxij．

(62)

刚性基础下桩与土竖向变形协调相等，即

εPzij=εszij．

(63)

利用式(63)和文献[4]中桩体横向变形系数kεij(即-εPxij/εPzij)，式(62)可变为：

εsxij=-kεijεszijm/(m-1)．

(64)

根据文献[5]结果可推算出土体竖向应变εszij及水平向应变εsxij分别与地基竖向附加应力增量σzij之间的关系，即：

εszij=

(65)

εszij=

(66)

式中：σzij可利用布辛奈斯克解[10]计算得到.由式(65)与(66)可知，散体材料桩复合地基沉降与桩土应力比Nij及桩体横向变形系数kεij有关，因此，有必要探讨Nij与kεij的确定方法.

首先，根据桩土边界水平向应力连续性可得：

σPxij=σsxij．

(67)

基于桩土模量比KEij(即EPij/Esij)的物理意义[4]，可利用式(46)及(52)求得：

KEij=KEi(j-1)αPijαsi(j-1)/[αsijαPi(j-1)]．

(68)

然后，将式(59)及(61)代入式(67)，并结合KEij的定义，可得：

Fij/KEij=(εPxij+μPijεPzij)/(εsxij+μsijεszij)．

(69)

式中：

Fij=(1+μPij)(1-2μPij)/[(1+μsij)(1-

2μsij)]．

(70)

将式(64)代入式(69)，并考虑kεij定义可得：

kεij=(1-m)(KEijμPij-μsijFij)/[KEij(1-m)

+Fijm]．

(71)

再根据桩土应力比Nij的定义，并利用式(58)和(60)可得：

Nij=KEi(j-1)[2μPijεPxij+(1-

μPij)εPzij]/{Fij[2μsijεsxij+(1-μsij)εszij]}．

(72)

利用式(66)和(67)并考虑kεij定义，化简式(72)可得：

1-μsij)]．

(73)

可见，利用式(73)可求得相应的桩土附加应力比.

由前述可知，计算复合地基沉降必须求解一系列非线性方程，且须进行反复迭代，下面介绍具体迭代方法.

4)变形参数及最终沉降的求解方法

(ⅰ)首先，设定第i地基压缩层桩与土在第j级增量荷载作用下的变形力学参数的初始值，其为该层桩土体在第j-1级增量荷载作用下的变形力学参数，同时，桩体横向变形系数kεij及桩土应力比Nij取该层桩土体在第j-1级增量荷载作用下的kεi(j-1)及Ni(j-1)，即：

(74)

(75)

(76)

(77)

(ⅳ)散体材料桩复合地基沉降计算

确定第i地基压缩分层在第j级荷载作用下竖向增量应变εszij之后，即可根据式(65)及沉降分析模型求得最终沉降，计算公式为：

(78)

3.2 不同埋深桩和土初始变形力学参数变化规律

一般情况下，散体材料桩复合地基中桩或土的初始变形力学参数可通过室内试验确定[10]，但是，此时的变形力学参数未考虑不同压缩分层已完成固结变形的不同，即未考虑地基应力历史或初始地应力对变形力学参数的影响，因此，必须建立散体材料桩复合地基桩或土初始变形力学参数的确定方法.

(79)

(80)

(81)

(82)

(83)

式中，

(84)

(85)

(86)

由式(81)～(86)可以看出，计算初始变形力学参数是一个递推计算过程，这里可参照本文3.1节求解方法得到第i地基压缩分层土体所受初始地应力加载完毕时初始变形力学参数，即：

(87)

(88)

(89)

按照上述思路，同样可得到考虑初始地应力影响下各压缩分层桩体初始变形力学参数的确定方法.

4 工程实例分析与验证

4.1 工程实例1

天津塘沽长芦盐厂载荷板试验资料[11]：载荷板面积为3 m×3 m，下压四根碎石桩，桩径0.8 m，桩长9 m，面积置换率m=0.223，桩和土体变形模量分别为4.528 MPa，0.716 8 MPa，桩体泊松比与孔隙率分别为0.25，0.07，土体泊松比与孔隙率分别为0.4，0.58，桩体重度为25 kN/m3，土体重度为18 kN/m3.试验荷载为88.2 kPa时压板实测最大沉降为82.0 mm.

计算深度按照规范[12]要求取7 m，可将地基压缩层分为7层,每层厚度为1 m，将附加荷载及自重荷载均分为20级加载.按3.2节方法计算考虑应力历史影响后的初始模量Esi0，EPi0，初始泊松比μsi0，μPi0，初始孔隙率nsi0，nPi0，计算结果见表1.将表1中初始变形力学参数代入3.1节，按3.1节方法和式(78)计算地基最终沉降量，同时采用现有其他方法计算，计算结果见表2.

表1 桩土变形模量初始值(1)

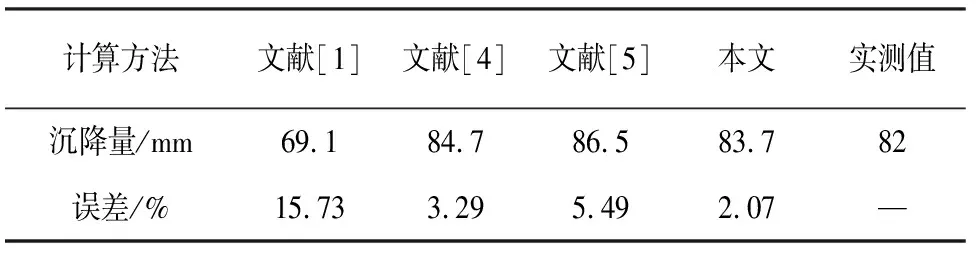
表2 复合地基沉降计算结果的比较(1)

4.2 工程实例2

某水库拦河大坝[13]所在的河床有较深的第4纪冲击层分布，用振冲碎石桩对地基加固.选取现场试验中BC-1组载荷试验曲线进行计算，该载荷板尺寸为1.8 m×1.8 m，桩体直径为1 m，长度为9 m，按正三角形布桩，面积置换率m=0.24.桩和土变形模量分别为3.5 MPa，1.5 MPa，重度分别为25 kN/m3，20 kN/m3.桩泊松比与孔隙率分别为0.25,0.07，土泊松比与孔隙率分别为0.40，0.52.试验荷载为108 kPa时压板实测最大沉降为42.0 mm.

计算深度按照规范[12]要求取9 m，将地基压缩层分为9层,每层厚度为1 m，将附加荷载及自重荷载均分为20级加载.按实例一计算过程，得桩土变形力学参数初始值见表3，沉降计算结果见表4.

表3 桩土变形模量初始值(2)

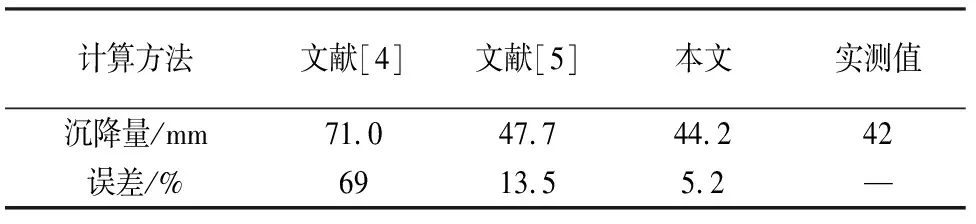
表4 复合地基沉降计算结果的比较(2)

从上述工程实例分析的过程和结果可以看出，采用本文方法计算的沉降值更接近地基沉降的实际观测值，表明本文方法具有较强的合理性和可行性.虽然本文方法与其他方法相比，计算精度虽然没有明显提高，但避免了地基土压缩试验曲线和经验系数的使用，还全面考虑了桩土变形力学参数变化对沉降的影响，因而具有明显的优越性.

5 结 论

1)从桩土受力与微观变形研究入手，建立了反映桩土表观变形力学参数与颗粒骨架实际变形力学参数之间关系的孔隙介质模型，较现有相关模型具有更广泛地应用范围.

2)考虑刚性基础下散体材料桩复合地基沉降特点，运用上述孔隙介质分析模型，引进分级加载思想，建立了附加应力和初始地应力对桩土变形力学参数的影响模型.

3)建立了反映桩土变形力学参数非线性变化特征的改进分层总和分析方法，其不仅反映了桩土变形力学参数随埋深和附加应力变化的特征，而且还能避免压缩试验曲线的使用.

[1] 盛崇文. 碎石桩复合地基的沉降计算[J]. 土木工程学报，1986,19(1):72-80．

SHENG Chong-wen. Estimation of settlement of composite ground reinforced by stone golunns [J]. China Civil Engneering Jounal, 1986,19(1): 72-80. (In Chinese)

[2] OMINE K, OHNO S. Deformation analysis of composite ground by homogenization method [C]//Proceedings of the Fourteenth International Conference on Soil Mechanics and Foundation Engineering.Rotterdam: Balkema A A,1997：719-722.

[3] 王凤池，朱浮声，王晓初. 复合地基复合模量的理论修正[J].东北大学学报，2003，24(5)：491-494.

WANG Feng-chi，ZHU Fu-sheng，WANG Xiao-chu. Theoretical analysis of the modulus of construction composite foundation[J]. Journal of Northeastern University，2003，24(5)：491-494．(In Chinese)

[4] 张定. 碎石桩复合地基的作用机理分析及沉降计算[J]. 岩土力学，1999，20(2)：81-86.

ZHANG Ding. Functional mechanism analysis and settlement computation on composite foundation of gravel pile [J].Rock and Soil Mechanics, 1999，20(2)：81-86 .(In Chinese)

[5] 曹文贵, 刘海涛, 张永杰. 散体材料桩复合地基沉降计算的分层总和法探讨[J]. 水利学报, 2010, 41(8): 984-990.

CAO Wen-gui, LIU Hai-tao ,ZHANG Yong-jie. Study on layer-wise summation method of settlement computation for composite foundation with friable material piles[J]. Journal of Hydraulic Engineering, 2010, 41(8): 984-990. (In Chinese)

[6] 卲龙潭,孙益振. 考虑孔隙变形的孔隙介质本构关系初探[J].岩土力学,2006,27(4):561-565．

SHAO Long-tan, SUN Yi-zhen. Primary tudy of stress-strain constitutive relation for porous media[J]. Rock and SoilMechanics,2006,27(4):561-565．(In Chinese)

[7] 徐芝纶.弹性力学[M].北京：高等教育出版社,2006：197-204．

XU Zhi-lun. Elastic mechanics [M]. Beijing: Higher Education Press, 2006：197-204．(In Chinese)

[8] 曹文贵,刘海涛, 张永杰.散体材料桩复合地基桩土应力比计算新方法[J]. 湖南大学学报:自然科学版, 2009, 36(7): 1-5.

CAO Wen-gui, LIU Hai-tao, ZHANG Yong-jie. A new pile-soil stress ratio calculation method of composite foundation with friable material piles[J]. Journal of Hunan University:Natural Sciences, 2009, 36 (7): 1-5. (In Chinese)

[9] 刘杰，赵明华，何杰. 碎石桩复合地基承载及变形性状研究[J]. 湖南大学学报:自然科学版, 2007, 34(5): 15-19.

LIU Jie, ZHAO Ming-hua, HE Jie. Research on bearing and deformation characters of composite foundation with granular columns[J]. Journal of Hunan University:Natural Sciences, 2007,34(5):15-19.(In Chinese)

[10]赵明华，俞晓,王怡荪. 土力学与基础工程[M]. 武汉: 武汉理工大学出版社, 2003:50-66．

ZHAO Ming-hua, YU Xiao, WANG Yi-sun. Soil mechanics and foundation engineering[M]. Wuhan: Wuhan University of Technology Press, 2003:50-66(In Chinese)

[11]方永凯,张鲁年,孟广训,等.振冲法加固塘沽软粘土地基[C]//软基加固新技术——振动水冲法．北京:水利电力出版社,1986.158-174.

FANG Yong-kai， ZHANG Lu-nian，MENG Guang-xun，etal. Vibrapunehing method reinforcement of soft clay foundation in Tanggu [C]//Soft Soil of New Technology-Vibration Jetting. Beijing: Water Power Press, 1986.158 -174. (In Chinese)

[12]GB 50007-2011建筑地基基础设计规范 [S].北京：中国建筑工业出版社，2011:54-55．

GB 50007-2011 Code for design of building foundation [S].Beijing: China Architecture and Building Press, 2011:54-55.(In Chinese)

[13]顿志林，高家美.弹性力学及其在岩土工程中的应用[M].北京：煤炭工业出版社，2003:295-370.

DUN Zhi-lin , GAO Jia-mei. Elastic mechanics and its application in the geotechnical engineering [M]. Beijing: Coal Industry Press, 2003:295-370.(In Chinese)