多级缸起竖系统运动可靠性评估的可视化方法

龙勇，袁静，高钦和，魏玉淼

(第二炮兵工程大学导弹发射与定向瞄准军队重点实验室，陕西西安710025)

复杂机械的可视化仿真作为一类传统而不断进步的研究领域，正向着高精密化和高自动化的方向发展。在液压系统传统的可靠性研究中，对液压系统的可靠性分析一般是指结构可靠性，主要是考虑机械结构的强度以及由于载荷的影响使之疲劳、磨损和断裂等引起的失效;而对于同样重要的机构运动可靠性则往往被忽略［1－2］。

机构可靠性要求在满足强度和刚度的可靠性要求基础之上，主要考虑机构在动作过程中由于运动学缺陷而引起的故障［3］;而机构运动可靠性是指机构精确、及时、协调地完成规定机械动作运动的能力，用概率表示就是机构运动可靠度。与一般可靠度定义略有差别的是，强调了精确、及时、协调，即强调了机构动作在几何空间中运动的精确度、在时间域内的准确性以及构件间的协调性、同步性要求［4］。

对于此类问题，采用传统的可靠性理论其分析和算法均比较麻烦。而且虽然目前国内外也有不少这方面的研究成果发表，但是其相关研究还没有达到系统而全面的程度［5－6］。以某大型液压起竖系统为例，提出一种基于可视化技术的运动可靠性仿真方法。

1 多级缸起竖系统概况

该起竖系统安装于某型发射平台的拖挂列车上，用于在有限时间内完成将负载由水平状态到垂直状态的起竖过程，同时避免对负载产生过大冲击。发射平台对液压起竖系统的设计提出了近乎苛刻的要求，表现在:(1)安装空间有限。整个系统留给液压油缸的安装空间非常狭小;(2)长行程。起竖系统的运动行程对相对安装空间来说，是后者的数倍;(3)变载荷。在整个时间区间内，负载是一个一阶导数连续时变的曲线;(4)由于负载对运动加速度较敏感，要求运动尽量平稳，但是战术指标要求起竖过程尽可能地快速。这一对矛盾对液压起竖系统的设计和安装造成了较大的困难。

很明显，首先要解决的是头两个困难，即狭小空间内的安装问题。为此设计了液压工程中较为少见的两组五级高速倒立液压油缸，于车体的两侧中部对称安装，下支点固定于车架，上支点与负载相连。如图1所示。油缸全部收缩时缸长符合第一点的空间限制，而五级缸体全部展开又能满足第二点的行程要求。起竖系统工作时，液压系统在程序控制下向两组油缸供应液压油，其流量是一组分段区间内连续的时变函数。油缸运动过程中，各级活塞杆依次伸出，并通过相邻两级相互间的碰撞来实现限位和换级，从而将负载起竖到设定角度。

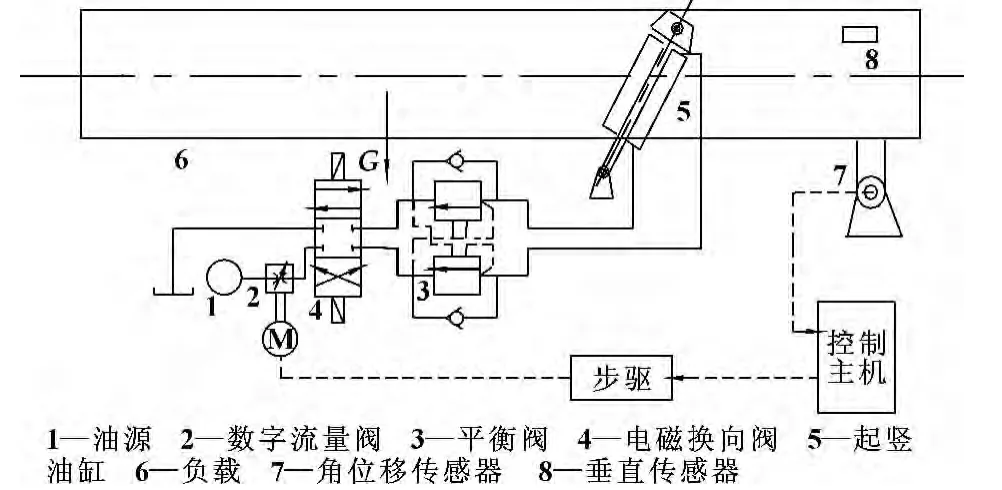
图1 液压起竖系统原理图

2 运动可靠性的可视化建模算法

双五级缸起竖系统的设计和制造非常复杂，如何确保它在不同负载情况下安全地工作，即起竖系统机构运动的可靠性是至关重要的，其中最重要的是液压油缸、负载和底盘三者构成的三角形在运动过程中是否保持良好的刚性铰接，不会因为某一边的长度变化产生脱胶现象。对此传统的液压系统可靠性领域有已经有了比较完整的一套理论，但大多侧重于从数值仿真的角度来计算空间内的位置超差，理论和算法都比较复杂。文中则引入可视化方法来仿真起竖过程，考察运动过程中的可靠性。假设油缸－底盘铰点和筒－底盘铰点固定，需要考察的是油缸－筒铰点的位置是否满足可靠性要求，具体算法如下:

步骤1，考虑到系统结构和运动规律以车体纵轴成对称分布，对其进行合理假设使之从空间模型简化为二维模型，为后续分析做准备。

步骤2，从相关文献直接引入起竖油缸的载荷－时间函数，作为第3、4步的源函数。

步骤3，从力学角度对简化后的机构模型进行受力分析，假定负载和底盘刚性铰接，推导出油缸载荷和筒旋转角度之间的函数关系。

步骤4，从运动学角度对简化后的机构模型进行运动关系推导，假定起竖油缸和底盘刚性铰接，推导出油缸载荷和油缸运动 (包括旋转角度、展长变化和子油缸换级)之间的函数关系。

步骤5，根据系统的几何尺寸和装配关系，对系统进行精确的可视化建模并生成视景。

步骤6，根据第3步得出的函数建立视景中的负载的旋转方程和初始铰点的坐标采样方程;根据第4步得出的函数建立视景中的油缸的运动方程 (包括旋转、展长和换级)和上铰点的坐标采样方程;

步骤7，设定时间同步点后启动仿真，设置合适的视角和分辨率，从视觉角度考察运动过程中油缸和负载的铰接情况。同时计算运动过程中油缸的上铰点和负载初始铰点二维坐标差值，从数学角度分析铰点是否超差。通过此两种手段来考察系统运动的可靠性。

3 系统运动模型建模

3.1 起竖系统模型的简化

起竖这一过程中有很多的变量，而作者所关心的是仅仅是起竖的运动学特性，为此必须做出适当简化:

(1)两个油缸各性能指标完全相同，液压系统在任意时刻对其泵入相同的流量。液压油对压力无形变，由此得出由四点支撑组成的四边形在任何时刻都是一个二维空间内的矩形，其两长边 (即油缸长度)L是唯一变量，是流量和缸体活塞面积的函数。

(2)两个油缸负载在任意时刻相同，且只承受轴向压 (拉)力。结合上面假设，可以把这一模型简化为二维平面内单油缸对1/2负载的作用过程。

3.2 油缸载荷－负载角度建模

首先从力学角度，直接分析和推导油缸载荷和负载角度之间函数关系。设负载质心为G，坐标为(x，y)，系统受力分析如图2，几何模型简化如图3所示［7］。

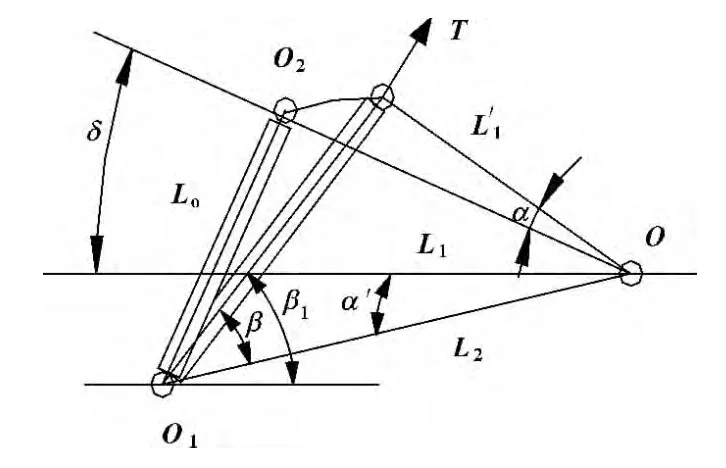
图2 系统的受力分析

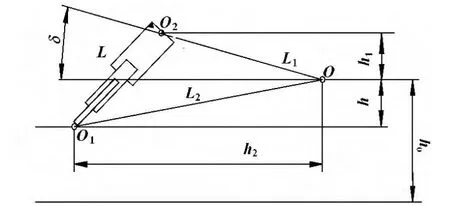
图3 起竖系统的几何结构简化

图中，油缸上下铰点为O1、O2，筒回转铰点为O，O1O2长度为L(初始长度为L0，全部伸出长度为Lm)，OO2长度为L1，OO1长度为L2。α为起竖角度，δ为OO2与水平的夹角 (起竖角)。α'为OO1与水平的夹角。其中T为油缸最终载荷函数，风载荷F则是与起竖角相关的随机函数，在此直接引用文献 ［7］内容。

在任一起竖角度α时，起竖油缸的受力应满足:

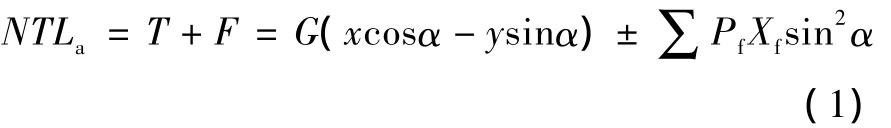
式中:N为起竖油缸的数量 (对于此例取N=2)，T为每个起竖油缸的受力，La为弹筒回转中心点O到起竖油缸的垂直距离，亦即液压缸受力的力臂。由三角形△O1OO2边角关系及正弦定理求得:

式中:L为起竖角α时油缸的长度，由余弦定理:

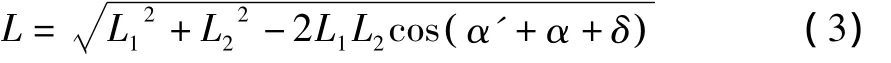
由式 (2)得:

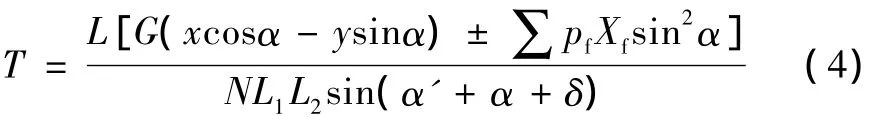
由式 (4)可得出起竖油缸的载荷T与起竖角α之间的函数关系，反映到可视化仿真中即可实现空载、配重弹、实弹等不同载荷时的起竖规律。

3.3 负载角度－起竖油缸参数建模

以下从运动学角度分析和推导负载和起竖油缸角度和展长之间的函数关系。具体而言，是以负载角度为自变量，分析起竖油缸的伸出长度、旋转角度和级数变化规律。

由于发射油缸是五级筒倒置安装，起竖时需要依次伸出四级筒，因此需要根据负载角度来控制当前级数及每级伸出长度。图3表示了起竖系统二维的三铰点式简化图，其中，下铰点O1到回转铰点O的距离为L2，水平距离为h2，设起竖油缸的初始长度为L0，全部伸出后的长度为Lm，根据此节开始的假设可知，在任何时候L1、L2、h0、h1、h2和α'都是不变的，而L和α则存在着单一的函数关系。

3.3.1 确定上铰点位置

设δi为油缸－筒铰点确定前的初始δ，可得油缸长度的两个极值L0和Lm为:

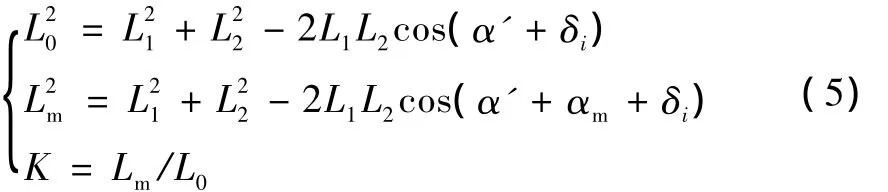
式中:αm为导弹垂直发射时的最大起竖角900，K为伸缩比。化简得:

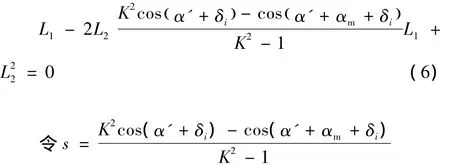
解方程求出满足伸缩比的O2的位置:

上式中，前支式油缸的s＞1，取正号，后支式起竖油缸的s＜1，取负号。由于系统为后支式起竖油缸，故。式中s含有未知量δi，求L1必须先对 δi赋值，而求得 L1后，根据式(6)求得δi:

一般情况下，先对δi角赋值，由式 (7)求出L1，再由式 (8)求出δ，两者是不等的。只要两者差值的绝对值小于给定的计算精度ε，此时求出的L1便是需要的L1，即满足|δ－δi|≤ε条件。起竖机构的三铰点位置得到后，用δ代替δi，由式 (5)就可以确定起竖油缸的初始长度Lo和全部伸出后的长度Lm。

3.3.2 根据负载T得到负载起竖角度α

至此，采用已知的起竖油缸负载的时变方程T=f(t)，联立如下方程得到T与α之间的函数关系:

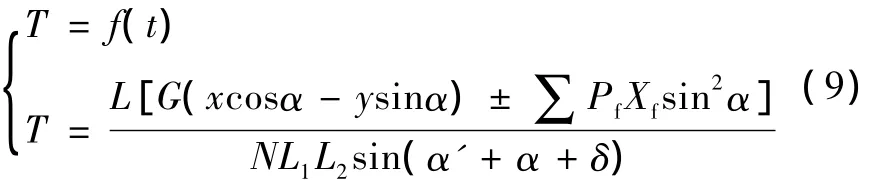
3.3.3 油缸总长度L－负载角度α方程

根据角度α得到任意时刻油缸长度L和角度α的关系为:

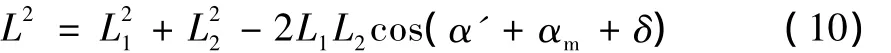
3.3.4 油缸的旋转角度β1－油缸总长度L方程

根据起竖油缸长度L得到起竖油缸的旋转方程为:

3.3.5 求取各级子油缸的运动方程和时序函数

根据起竖油缸各级的动作时序放程和长度L得到各级缸体的运动方程，由于在四级缸体是按照4－3－2－1的顺序依次伸出，油缸的换级是通过判断当前级是否伸展到为标准的，因此只需将第3.3.3节得出的油缸总长度L与当前级的当前长度和上一级的到位长度相比较，如果相等则作为当前级到位并下一级伸出的条件即可，据此可以得出油缸的换级时序函数，在此不加以展开，仅给出部分的VC程序如下:

4 系统的可视化建模

液压起竖系统的可视化能够更加直观地验证液压起竖系统的运动可靠性，主要包括以下步骤:

步骤1，分别建立底盘、油缸组和负载精确的三维CAD模型，其他附属模型和贴图则采用Creator建模。

步骤2，按照第3.1节定义的空间关系给出的起竖前初始姿态，计算三个铰接点的空间坐标，在CAD内进行精确的虚拟装配。

步骤3，通过专门工具将CAD模型转化为OPENFLIGHT格式模型，并载入到可视化引擎VEGA中进行仿真，这时图3中平台、油缸和负载形成了三角形OO1O2，其中平台、油缸在点O1铰接，负载、平台在点O铰接，而油缸、负载在点O2则没有铰接，并将仿真前负载上与点O2相对应的点设为O'2。

步骤4，在VC中编制可视化驱动程序，其中负载的运动规律依据第3.3.2节中给出的负载－筒体旋转角度方程执行，而液压油缸的运动规律则按照第3.3.3节和第3.3.4节执行。

步骤5，通过以上过程，利用外部输入的负载函数来驱动整个系统的可视化模型，执行负载起竖过程。调整合适的观察分辨率，考察在运动过程中，油缸、负载在较直观的视觉尺度上是否在O、O1和O2三点产生脱铰现象，更进一步地，计算O2和O'2在运动时空间坐标误差，从而在数学尺度上进一步验证系统的运动可靠性。

基于以上步骤，进行了某起竖系统的数学建模及可视化仿真。实际运行证明:该液压系统的运动安全性在视觉尺度上令人满意，没有出现铰点脱铰现象。图4给出了起竖到60°时的状态截图。

图4 发射筒－起竖油缸的运动可视化仿真截图

5 结语

针对复杂系统的运动可靠性仿真问题，将可视化仿真引入可靠性分析技术中，提出一种基于可视化仿真的复杂机械系统的运动可靠性分析方法。以统一的原始模型为起点，分别从力学角度和几何学角度分析系统的运动规律，并将所得模型引入可视化仿真中，从视觉角度直观地考察系统的运动状态及其可靠性。该方法为复杂机械和液压系统的可靠性分析技术提供了一种新的方法，对于其他系统的可靠性分析也具有一定的借鉴意义。

【1】孙志礼，陈良玉．实用机械可靠性设计理论与方法［M］．北京:科学出版社，2003．

【2】李锋．某系统的动态建模与优化研究［D］．西安:第二炮兵工程学院，2004．

【3】高钦和，黄先祥．多级缸起竖系统运动过程的建模与仿真［J］．系统仿真学报，2005，17(7):1563 －1566．

【4】沈海军，郭万林．结构疲劳寿命、可靠性可视化技术与虚拟疲劳设计［J］．机械设计，2003，20(3):20 －22．

【5】胡启国，刘依路．考虑中介状态和失效相关时机械系统的可靠性分析［C］//Proceedings of 2012(Shenyang)International Colloquium on Safety Science and Technology，2012:36－42．

【6】杨腾达，孙川．机械系统可靠性模糊预计的可视化设计［J］．黄石理工学院学报，2011，27(4):18 －23．

【7】袁锦虎，邓虹，黄毅勇．三维可视化水工设计的系统框架和集成研究［J］．水利与建筑工程学报，2009，7(1):84－92．