风洞模型支撑装置驱动油缸位置和速度的精确控制研究
刘念,王帆,褚卫华,李树成
(中国空气动力研究与发展中心空气动力学国家重点实验室,四川绵阳621000)
在风洞试验中,模型支撑装置用以支撑试验模型,实现姿态的调节,模拟实际运动时的运动学与动力学特征,从而获得重要的试验数据,其性能的好坏直接关系到试验的质量。
随着风洞尺寸和马赫数的增加,模型支撑装置的负载也随之增大。电液伺服系统综合了电气和液压两方面的优点,特别适合于模型支撑装置负载质量大、要求响应速度快的特点,因此在风洞中得到广泛的应用。风洞模型支撑装置电液伺服系统常采用阀控非对称缸形式[1],通过电液流量伺服阀控制非对称液压缸,驱动机构实现模型姿态的调节。
众所周知,模型支撑装置角度机构的调节方式分为步进式和连续式两种[2]。以迎角机构为例,步进变迎角要求驱动油缸能阶梯精确定位于任意位置,在定位过程中,油缸速度没有精度要求;连续变迎角要保证迎角以某一恒角速度连续变化。一般情况下,液压缸活塞位置和速度与模型姿态角度和角速度之间是非线性关系,要实现连续变姿态角,必须精确控制油缸的非线性速度。由于液压系统存在驱动对象惯性大、油液具有压缩性等固有特点,要实现油缸速度的精确控制很难。
针对上述特点,作者搭建了模拟风洞模型支撑装置的简易杆支撑机构电液伺服控制系统,并采用速度位置复合控制策略,通过仿真和试验研究,实现了驱动油缸位置和速度的同时精确控制。
1 系统组成
杆支撑机构电液伺服控制系统组成如图1所示,主要由油源、驱动油缸、杆支撑机构、电液流量伺服阀、压力传感器、磁致伸缩位置/速度传感器、伺服放大器、NI PXI嵌入式实时控制系统和上位工控机组成。驱动液压缸缸径φ100 mm,活塞杆径φ50 mm,行程1 000 mm。电液流量伺服阀型号为FF106-63,单边压差10.5 MPa时,额定流量为63 L/min,额定电流15 mA。伺服放大器型号为MOOG G122-824-2 PI,输入控制电压-10~+10 V,输出电流增益可调。位移传感器型号为MTS RPS-1000M-R10-1-A01-0005,带位置和速度双输出,位置分辨率0.015 mm,速度分辨率0.1 mm/s。
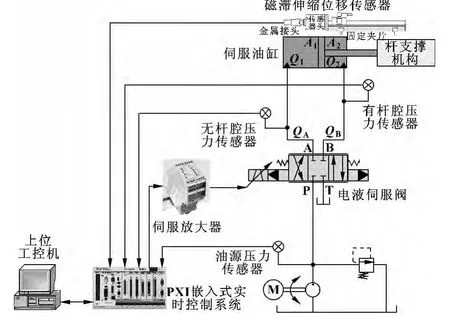
图1 系统组成
杆支撑机构见图2(a),伺服油缸驱动支杆绕支杆座旋转,模拟风洞中最常见、控制精度要求较高的迎角机构。杆支撑机构运动关系示意图如图2(b)所示。
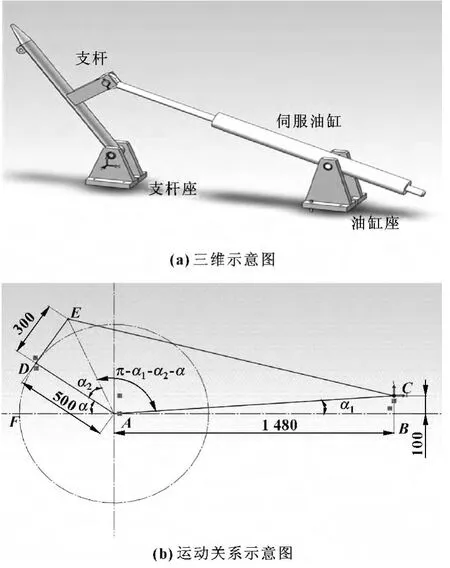
图2 杆支撑机构
油缸中部耳轴中心与活塞杆端部单耳环中心距离CE满足下式
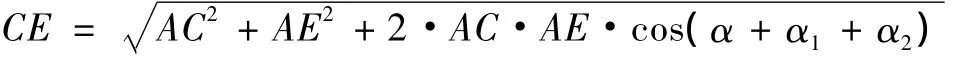
其中:AB=1 480 mm,BC=100 mm,AD=500 mm,DE=300 mm;α为迎角,油缸活塞杆收回时角度增大,单位 (°)。
记 AC=a,AE=b,α1+α2=α0,则
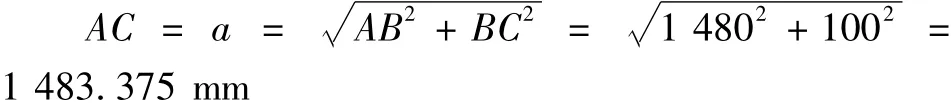

当油缸活塞杆完全收回时,CE=1 000 mm。设油缸活塞位置 (即油缸活塞杆伸出长度)为x,则α与x有如下关系
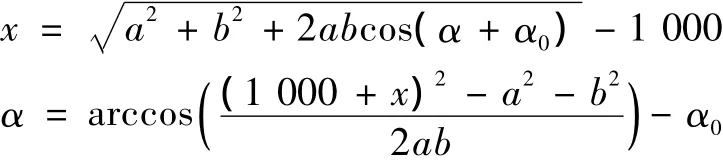
图3示出了迎角α与活塞位置x的关系曲线。可见:迎角范围约为-2°~118°。
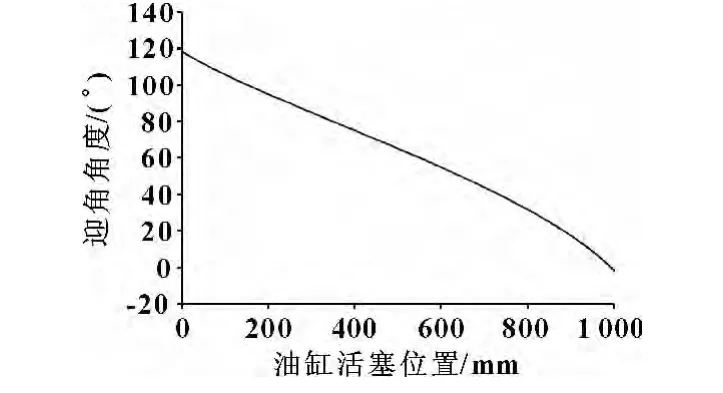
图3 迎角与油缸活塞位置关系曲线
迎角增量dα与活塞位置增量dx的关系为
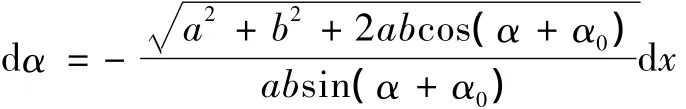
令dα=0.02°,可得活塞定位精度曲线,如图4所示。可见:要保证迎角0.02°的定位精度指标,极限情况下,活塞的定位精度需达到0.08 mm。极限位置出现在活塞位置x=1 000 mm处,即油缸活塞杆完全伸出时。
进一步,迎角角速度dα/dt与油缸速度dx/dt的关系为
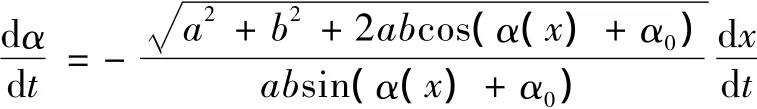
从图5可以看出迎角角速度与活塞速度和位置呈非线性关系,要保证迎角以恒角速度连续变化,就必须精确控制油缸非匀速连续变化。
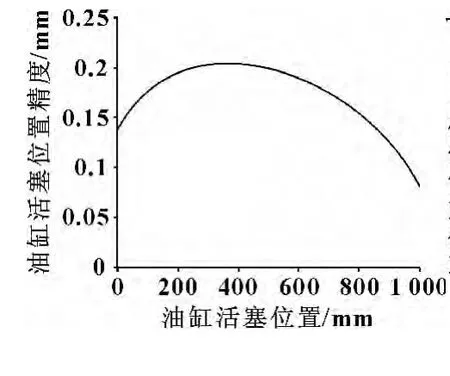
图4 对应0.02°时油缸活塞定位精度曲线
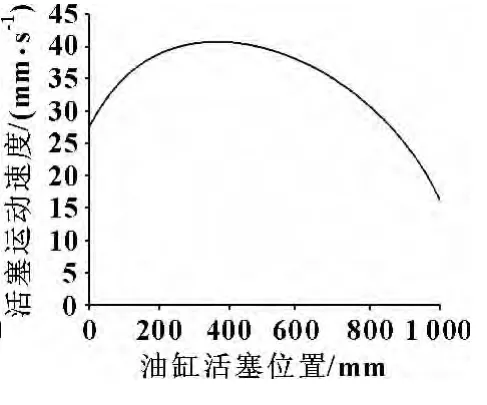
图5 4°/s连续变迎角时迎角角速度与活塞速度和位置关系
2 速度/位置复合控制策略
为了实现驱动油缸位置和速度的同时精确控制,采用速度前馈和位置反馈复合控制方法,即在位置反馈的基础上,增加速度前馈,将期望速度对应的控制信号叠加在伺服阀控制信号上[3]。
速度前馈和位置反馈复合控制原理图速度/位置反馈复合控制系统框图如图6所示。图中,速度/位移信号发生器根据初始迎角、目标迎角、工作曲线类型及运动参数生成油缸期望的速度曲线vr和位移曲线yr;速度前馈计算模型根据期望速度曲线vr和系统实际压力pA、pB、pS计算出相应的前馈控制量Uv;Kv为速度前馈系数;位置反馈采用比例控制,Kp为位置反馈系数,输出为Up;UvKv与Up之和Uc为伺服阀总的控制信号;pA、pB分别为伺服阀A口和B口压力,pS为油源压力。
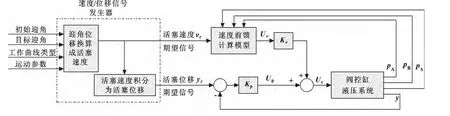
图6 速度前馈和位置反馈复合控制原理图
2.1 速度前馈计算模型
约定单伸杆液压缸活塞杆伸出为正方向,下面推导油缸正向运动时速度前馈量计算模型。
假定伺服阀A口与液压缸无杆腔相连。用Q1表示液压缸无杆腔吸入或排出的流量,QA表示伺服阀A口的流量。为了用公式统一表达,流量符号作如下约定:油液由伺服阀P口流向A口时,无杆腔进油,此时Q1和QA为正;反之,油液由A口流向T口时无杆腔排油,此时Q1和QA为负。这样有

在上述约定下,并忽略液压缸的泄漏,液压缸无杆腔流量和活塞杆的速度关系可表示为

式中:Q1为液压缸无杆腔流量,L/min;
v为液压缸活塞杆速度,m/s;
A1为液压缸无杆腔活塞面积,mm2。
根据产品手册,伺服阀在控制信号为额定电流Ia(单位mA)时,若单边额定压差ΔpN时的额定流量为QN,则压差为Δp时的流量为

设伺服阀控制电流信号为xIa,x(-1≤x≤1)为伺服阀控制信号相对值。忽略伺服阀的零位泄漏,并假设流量曲线为线性,则x>0时,活塞杆的运动为正向 (v>0),由式 (3)得出此时A口流量计算公式为

令速度前馈控制量Uv=x,并将式 (2)— (4)代入式 (1)并整理,得
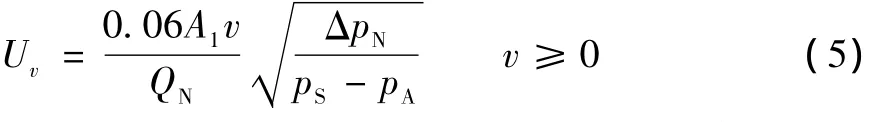
同理,可以得出活塞杆反向运动时速度前馈控制量Uv计算公式
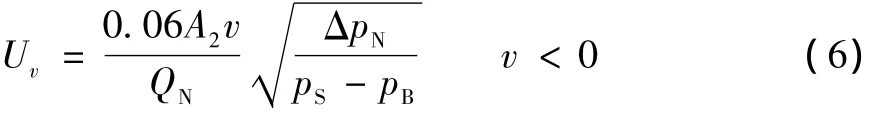
式中:A2为液压缸有杆腔活塞面积,mm2。
结合式 (5)和 (6),并用期望速度vr代替其中的速度v,即得到速度前馈控制量Uv计算模型
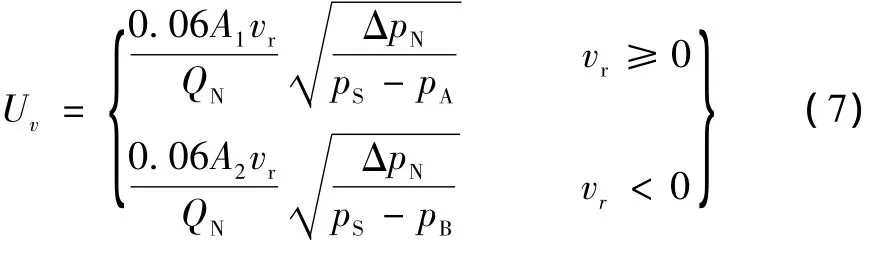
在上述速度前馈模型中,pS-pA和pS-pB包含了力负载的信息:负载相同时期望速度不同,则前馈控制量Uv不同;负载变化时,即使期望速度vr相同,前馈控制量Uv也不同,自动适应负载的变化。
电液伺服系统中,伺服放大器一般为深度电流负反馈型,其输入电压 (单位V)和输出电流 (单位mA)成比例关系,传递函数为
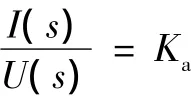
式中:Ka为电压电流转换系数,即功率放大增益,mA/V。
由原理图6可知,在位移反馈系数Kp=0,仅有速度前馈控制时,下式应成立
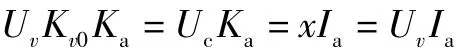
此时速度前馈系数Kv0满足

位置反馈和速度前馈同时工作时,Kv应略小于Kv0,以防止速度存在过冲现象。
2.2 速度位移信号发生器
在速度/位置复合控制系统中,速度前馈在动态运行过程中起主要作用,位置反馈在期望位置附近起主要作用,二者的无扰切换通过合理设计速度和位移给定曲线实现。
由于实际液压执行机构运动时,其工作过程可分为3个步骤:启动过程、中间运行过程、制动定位过程。为此设计了两种工作曲线:梯形速度曲线和抛物形速度曲线[4]。
梯形速度曲线以加速度am和最大速度 (稳速)vmax为运动参数。加速启动过程加速度为常数,稳速过程加速度为零,运动始末速度为零,如图7所示。
抛物线型速度曲线以加速时间ta和最大速度(稳速)vmax为运动参数。加速度在加减速过程中为三角形变化,加速度变化率为常数,如图8所示。
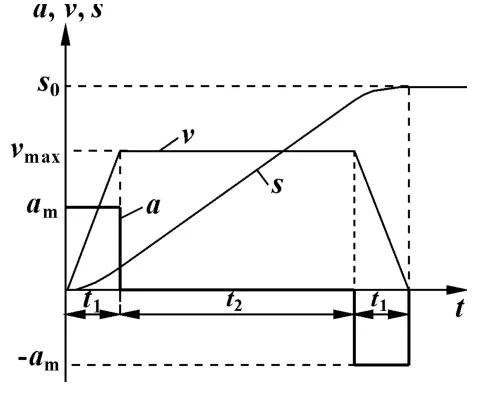
图7 梯形速度曲线
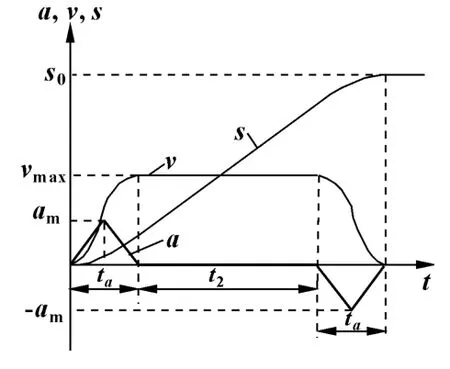
图8 抛物形速度曲线
如果直接以期望位置作为位置反馈的给定输入信号,则在动态运行过程中位置误差较大,从而使位置反馈回路控制输出较大,与速度前馈控制同时起作用,无法实现运行速度的控制。以速度给定信号的积分作为位移给定信号,使整个动态运行过程中位置误差都较小,保证速度前馈控制起主要作用,从而控制运行速度。
由给出的期望速度曲线计算速度前馈控制量,由位移给定值和位移传感器反馈回的实际位移值计算运动偏差进行补偿。在整个运行过程中,前馈控制量由零逐渐增大,再逐渐减为零,实现了与位置环控制的无扰切换。
3 机电液联合仿真研究
杆支撑机构电液伺服系统是典型的机电液一体化复合系统。采用AMESim/Motion联合仿真技术,借助AMESim和Motion分别创建系统的电液控制模型和机械运动模型,并利用两软件间的接口交互位置、速度和力信息,可以实现机电液系统的联合仿真[5-6]。
利用AMESim/Motion创建杆支撑机构电液伺服系统的机、电、液仿真模型如图9所示。根据系统实际数据设定相关参数,油源工作压力8 MPa。
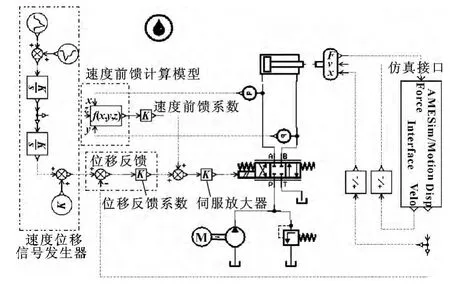
图9 杆支撑机构电液伺服系统联合仿真模型
由式 (7)可得,速度前馈量计算公式为
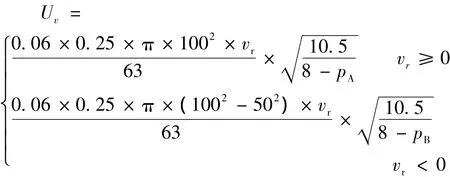
设定伺服放大器功率增益Ka=1.5,由式 (8)可得:在仅有速度前馈时,Kv0=Ia/Ka=10。图10示出了采用梯形速度曲线,am=10 mm/s2,vmax=20 mm/s,不同Kv、Kp下,油缸阶梯定位的仿真结果。
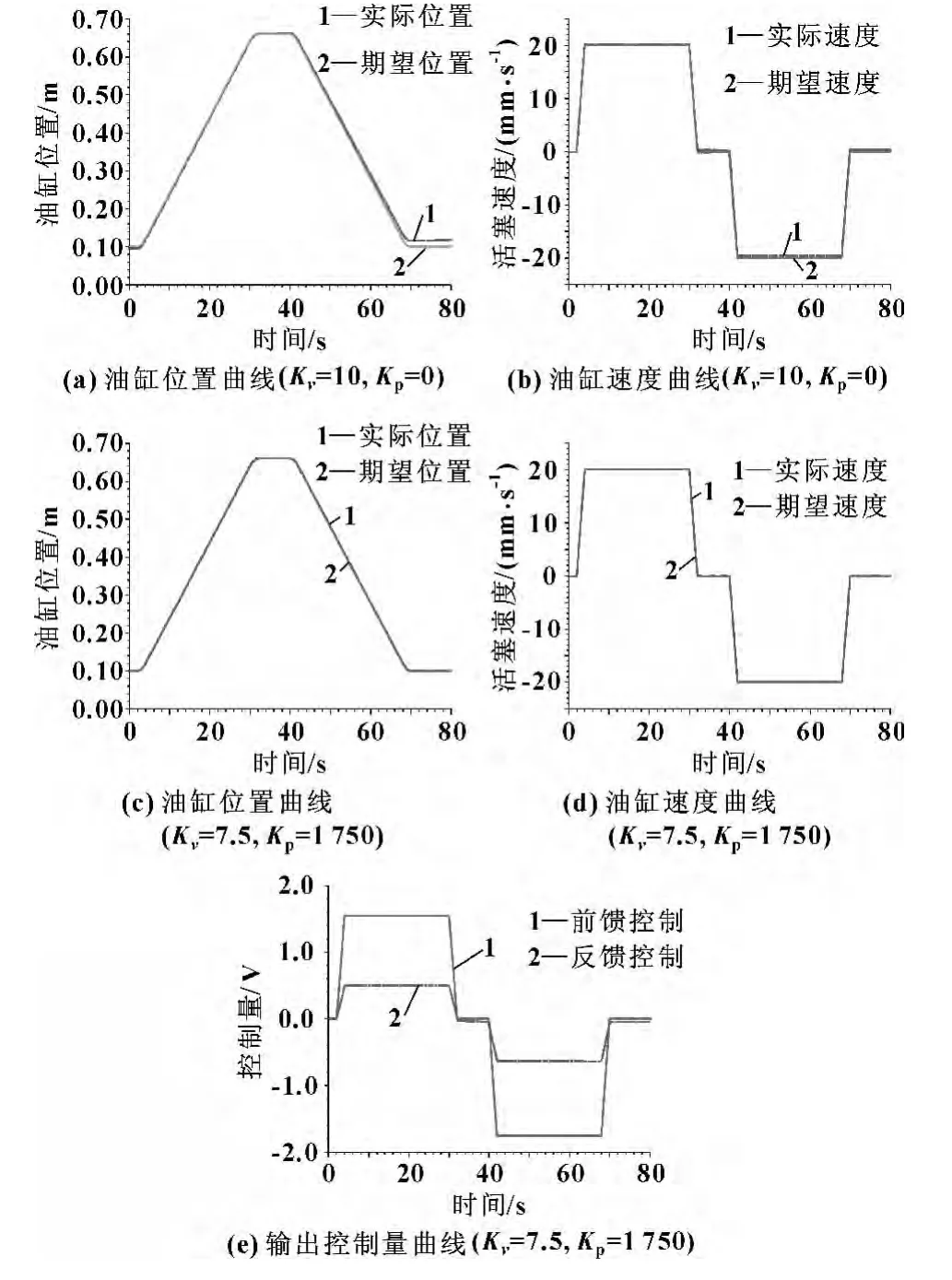
图10 仿真结果
分析如下:
(1)Kv=10,Kp=0时,系统仅有速度前馈,属于开环控制。由图10(a)与图10(b)可以看出:若令Kv=Kv0=10,仅采用速度前馈控制,即可大致实现油缸位置和速度的跟随,但由于各种干扰,跟随误差会被累积,且无法消除。
(2)Kv=7.5,Kp=1 750时,速度前馈和位置反馈同时工作,由图10(c)至图10(e)可以看出,油缸位置和速度响应曲线与期望曲线基本重合。在油缸动态运行过程中,速度前馈部分控制量起主要作用,实现油缸位置和速度的快速跟随,此时位置反馈控制量起修正位置和速度偏差的作用;在定位过程中,前馈控制部分输出为零,反馈控制部分输出起作用,用于油缸的精确定位。
(3)采用速度/位置复合控制策略,在变负载下,对于正反向,采用相同的控制参数,速度和位置控制都能达到很好的性能,证明了速度前馈量计算模型的合理性和有效性。
4 试验研究
试验中设定油源压力为8 MPa。由于没有安装编码器,以下所有迎角值均通过活塞实际位移值计算得出。
针对梯形速度曲线,图11示出了机构迎角从15°运动到80°时的试验结果,其中 am=10 mm/s2,vmax=20 mm/s,Kv=7.5,Kp=1 750。由图可见:油缸匀速运行阶段,位置动态跟随误差小于0.08 mm,对应迎角跟随误差小于0.02°,油缸稳态速度控制精度小于1%,此时速度前馈起主要作用,负责油缸位置的快速跟随;油缸定位阶段,稳态位置偏差小于0.04 mm,对应迎角定位偏差小于0.004°,此时速度前馈量为零,位置反馈起主要作用,负责油缸的精确定位。
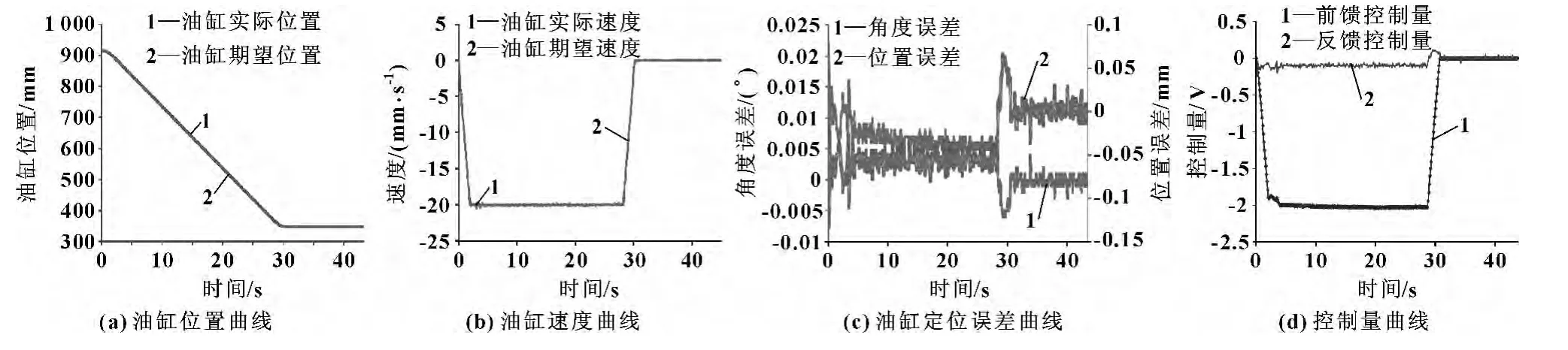
图11 梯形速度曲线阶梯定位试验结果
图12给出了Kp=2 000时,不同Kv下油缸位置跟随效果。由图可见:
(1)无速度前馈时 (即Kv=0,此时仅有位置反馈),油缸位置动态跟随误差达1.1 mm,当Kv=7.5时 (此时速度前馈起主要作用),油缸位置动态跟随误差小于0.04 mm。这表明,与仅采用位置反馈相比,采用速度前馈加位置反馈策略可以实现油缸位置的“精确”跟随。
(2)位置反馈系数固定不变时,存在一个最优的速度前馈系数值,使得油缸位置动态跟随误差最小。
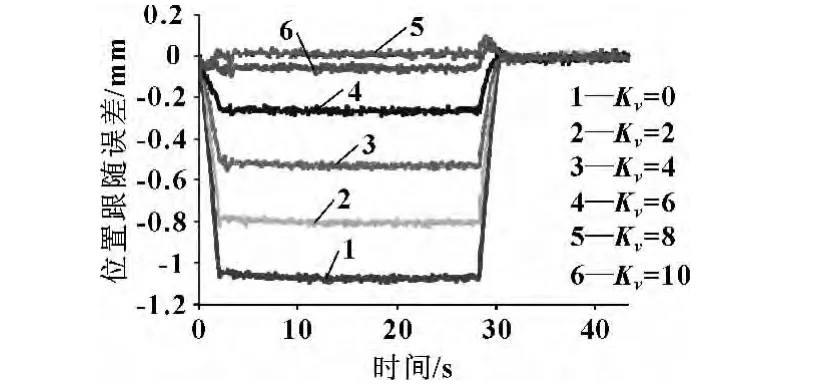
图12 不同Kv下油缸位置跟随效果 (Kp=2 000)
针对抛物形速度曲线,图13示出了机构迎角从80°运动到10°时的试验结果,其中ta=5 s,vmax=50 mm/s,Kv=7.5,Kp=2 000。由图可见:油缸匀速运行阶段,位置动态跟随误差小于0.3 mm,对应迎角跟随误差小于0.04°;定位阶段,稳态位置偏差小于0.05 mm,对应迎角定位偏差小于0.01°。油缸实际速度基本与期望速度重合,稳态控制精度优于1% 。
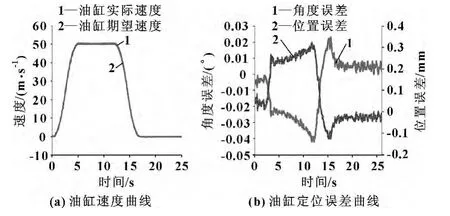
图13 抛物形速度曲线阶梯定位试验结果
图14示出了机构以4°/s匀角速度从80°运动到10°连续变迎角时的试验结果,其中角速度采用梯形曲线,角加速度d2α/dt2=2°/s2,角速度 (dα/dt)max=4°/s,Kv=9.5,Kp=2 000。由图可见:连续变迎角时,采用速度位置复合控制策略,油缸实际速度基本与非线性的期望速度重合,速度控制精度小于0.4 mm/s,对应迎角角速度控制精度优于1%,可以满足风洞迎角机构连续变迎角试验的需要。
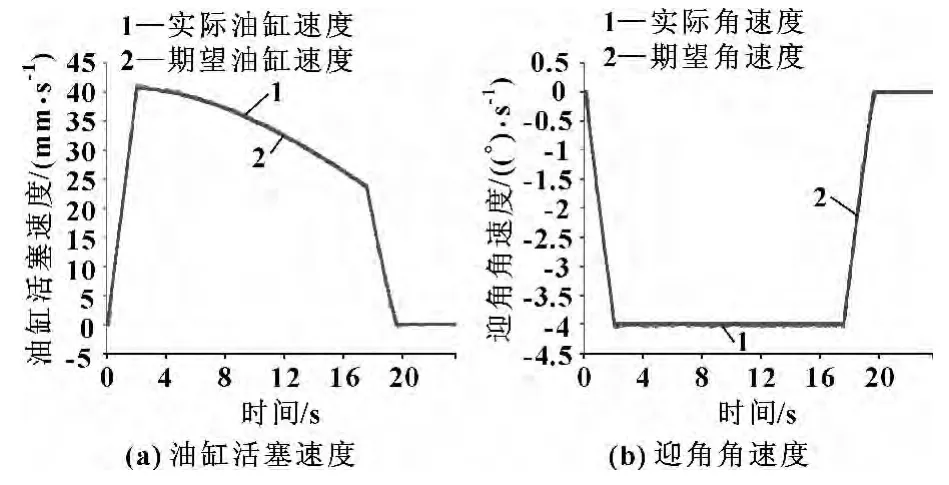
图14 连续变迎角试验结果
5 结束语
针对风洞模型支撑装置驱动油缸要求位置和速度同时精确控制的特点,搭建了简易的杆支撑机构电液伺服系统。采用速度前馈和位置反馈复合控制策略,详细推导了速度前馈计算模型,并设计了两种合理的速度曲线,通过速度位移信号发生器,实现了速度前馈控制和位置反馈控制的无扰切换。借助AMESim/Motion联合仿真技术,创建了杆支撑机构电液伺服系统的机电液仿真模型。理论推导、仿真研究与试验结果相互印证,证实了速度前馈和位置反馈复合控制策略的有效性,可以实现油缸位置和速度的同时精确控制。所采用的控制策略简单,容易实现,具有重要的工程应用价值,可以广泛用于风洞模型支撑装置步进和连续变姿态角控制中。
【1】王帆,周平,葛思华,等.一种新型快速位置系统的研究[J].机床与液压,1996(2):13 -14.
【2】孙海生,祝明红.φ3.2 m风洞战斗机大迎角试验关键技术研究[J].实验流体力学,2011(3):52-57.
【3】柏艳红,权龙.电液位置速度复合伺服系统控制策略[J].机械工程学报,2010(24):150 -155.
【4】徐格宁,胡增嵘.电梯速度曲线、行程及时间综合分析[J].中国工程机械学报,2004(4):413 -416.
【5】付永领,祁晓野.LMS Imagine.LabAMESim系统建模和仿真:参考手册[M].北京:北京航天航空大学出版社,2011.
【6】刘念,李树成,王帆.基于Motion/AMESim的某风洞迎角机构建模与仿真研究[J].机床与液压,2012,40(11):135-137.

