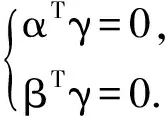关于矩阵对角化的探讨

张立卓

(对外经济贸易大学 统计学院，北京 100029)

众所周知，在复数域C上，若设n阶矩阵A的不同的特征值为λ1,λ2,…,λt，其重数分别为ki(i=1,2,…,t)，则k1+k2+…+kt=n.关于矩阵A与对角矩阵相似有下列等价命题：

(i)n阶矩阵A与对角矩阵相似(即A可对角化)的充分必要条件是A有n个线性无关的特征向量.

(ii)n阶矩阵A与对角矩阵相似的充分必要条件是A的对应于特征值λi(i=1,2,…,t)的线性无关特征向量的个数都恰好等于其重数ki.

(iii)n阶矩阵A与对角矩阵相似的充分必要条件是A的对应于ki重特征值λi(i=1,2,…,t)，秩r(λiE-A)=n-ki.

下面通过示例介绍上述关于矩阵对角化的判别方法在具体问题中的使用.

例1设实数域上n维向量空间n(n≥3)中的向量α，且αTα=a，矩阵A=ααT，求可逆矩阵P，使P-1AP=Λ，并写出该对角矩阵Λ.

分析 要找出A的n个线性无关的特征向量，可先考查α，再考查与α正交的向量.

解由题设，AT=(ααT)T=ααT=A，A为实对称矩阵，必相似于对角矩阵.

(i) 如果αTα=a=0，即α=0，则A=ααT=O. 于是取任一n阶可逆矩阵P，有

(ii) 如果αTα=a>0，即α≠0，则

Aα=(ααT)α=α(αTα)=aα，

所以λ1=a为A的一个特征值，α为对应λ1=a的线性无关的特征向量.设β=(x1,x2,…,xn)T∈n，建立齐次线性方程组，

αTβ=0.

因r(αT)=1可知，其基础解系应含n-1个解向量，设其分别为β2,β3,…,βn，满足

αTβ2=αTβ3=…=αTβn=0，

从而

Aβi=(ααT)βi=α(αTβi)=0=0βi(i=2,3,…,n)，

所以λ2=0为A的又一特征值，β2,β3,…,βn为对应λ2=0的线性无关的特征向量，因此特征值λ2=0的重数应为n-1.又因为矩阵的属于不同特征值的线性无关特征向量必线性无关，即α,β2,β3,…,βn线性无关，令矩阵P=(α，β2，β3，…，βn)，则P为n阶可逆矩阵，且使

拓展 如果设矩阵B=kE+lA=kE+lααT，E为n阶单位矩阵，k,l为任意非零实常数，αTα=a(a>0)，则同理可推得B可对角化，且

P1为本例所求的可逆矩阵.

注 事实上，若n阶矩阵A相似于对角矩阵，即存在一个可逆矩阵P，使

A的多项式为φ(A)=a0Am+a1Am-1+…+am-1A+amE(m为正整数)，则矩阵φ(A)可对角化，且

这是因为

其中k=1,2,…,m. 于是

P-1φ(A)P=P-1(a0Am+a1Am-1+…+am-1A+amE)P

=a0P-1AmP+a1P-1Am-1P+…+am-1P-1AP+amP-1EP

=a0Λm+a1Λm-1+…+am-1Λ+amE

这表明若n阶矩阵A可对角化，则A的多项式φ(A)也可对角化.

例2设向量空间n(n≥3)的向量α与β正交，且αTα=a,βTβ=b，矩阵A=ααT+ββT，求可逆矩阵P，使P-1AP=Λ，并写出该对角矩阵Λ.

分析 可验证α与β是特征向量. 再由|A|=0，求出A的其余线性无关的特征向量.

证由题设，AT=(ααT+ββT)T=ααT+ββT=A，A为实对称矩阵，必相似于对角矩阵，

(i) 如果αTα=a=0,βTβ=b=0，即α=0,β=0，则A=O. 于是取任一n阶可逆矩阵P，有

(ii) 如果αTα=a≠0,βTβ=b=0，即α≠0,β=0，则A=ααT. 据上例结论，存在n阶可逆矩阵P1，使

(iii) 如果αTα=a=0,βTβ=b≠0，即α=0,β≠0，则A=ββT. 同理存在n阶可逆矩阵P2，使

(iv) 如果αTα=a≠0,βTβ=b≠0，即α≠0,β≠0. 由已知αTβ=0=βTα，于是

Aα=(ααT+ββT)α=aα.

所以λ1=a是A的一个特征值，α为对应的线性无关的特征向量，

Aβ=(ααT+ββT)β=bβ，

λ2=b是A的又一个特征值，β为对应的线性无关的特征向量. 又因为

r(A)=r(ααT+ββT)≤r(ααT)+r(ββT)≤r(α)+r(β)=1+1=2

Aγi=(ααT+ββT)γi=O=0γi(i=3,4,…,n)，

即γ3,γ4,…,γn为A的对应于特征值λ3=0的线性无关的特征值向量，于是特征值λ3=0的重数应为n-2，且α,β,γ3,γ4,…,γn线性无关. 令矩阵P3=(αβγ3γ4…γn)，则P3为n阶可逆矩阵，使

拓展 如果设矩阵B=kE+lααT+mββT，E为n阶单位矩阵，k为任意实常数，l,m为任意非零实常数，αTα=a>0,βTβ=b>0，则同理可推得B可对角化，且

P3为本例所求的可逆矩阵.

例3设向量空间n(n≥3)的非零向量α,β，矩阵A=βαT，问A是否可对角化？如果A可对角化？求出可逆矩阵P，使P-1AP为对角矩阵，并写出对角矩阵.

分析 可依α与β是否正交分别讨论.

解(i) 若αTβ=0，则A2=(βαT)(βαT)=β(αTβ)αT=O，A为幂零矩阵. 设λ为A的特征值，则

Aγ=λγ(γ≠0),A2γ=λ2γ=0，λ=0，

即幂零矩阵A的特征值全为零. 又α,β是非零向量，即A=βαT≠O，r(A)≥1，同时r(A)=r(βαT)≤r(β)=1，即r(A)=1，于是方程组AX=0的基础解系含n-1个解向量，表明矩阵A没有n个线性无关的特征向量，故A不可对角化.

(ii) 若αTβ=a≠0，由题设，β≠0，

Aβ=(βαT)β=β(αTβ)=aβ，

λ1=a是A的特征值，β为对应λ1=a的线性无关的特征向量.由(1)知，r(A)=1，于是方程组AX=0的基础解系含n-1个解向量，设其为β2,β3,…,βn，满足

Aβi=0=0βi(i=2,3,…,n)，

β2,β3,…,βn为A的属于特征值λ2=0的线性无关的特征向量，因此特征值λ2=0重数应为n-1，且β,β2,β3,…,βn线性无关，即A有n个线性无关的特征向量，故A可对角化.令矩阵P=(β，β2，β3，…，βn)，则P为n阶可逆矩阵，使

拓展 如果设矩阵B=kE+lA=kE+lβαT，E为n阶单位矩阵，k,l为任意实常数，αTα=a>0，则同理可推得B可对角化，且

P为本例所求的可逆矩阵.

例4设向量空间n(n≥3)的向量α与β正交，且αTα=a,βTβ=b，矩阵A=αβT+βαT，求可逆矩阵P，使P-1AP=Λ，并写出该对角矩阵Λ.

分析 若α,β之一为零向量，则A=O.若α,β均不为零向量，则可验证α-β，α+β是特征向量，再由r(A)=2求出其余线性无关的特征向量.

证因为AT=(αβT+βαT)T=βαT+αβT=A，所以A为实对称矩阵，必可相似于对角矩阵，

(i) 如果αTα=a=0=βTβ，即α=0，β=0，此时A=O. 于是取任一n阶可逆矩阵P，有

(ii) 如果αTα=a≠0且βTβ=a≠0，即α≠0,β≠0. 由已知α,β是正交向量组，α与β必线性无关，因此α+β≠0,α-β≠0，

Aα=(αβT+βαT)α=aβ，Aβ=(αβT+βαT)β=aα，

A(α-β)=aβ-aα=-a(α-β)，

所以λ1=-a为A的一个特征值，α-β为λ1=-a对应的线性无关的特征向量，

A(α+β)=aβ+aα=a(α+β)，

所以λ2=a为A的又一个特征值，α+β为λ2=a对应的线性无关的特征向量. 又因为A可对角化，所以A的秩等于A的非零特征值的个数，因此r(A)≥2. 又

r(A)=r(αβT+βαT)≤r(αβT)+r(βαT)≤r(α)+r(β)=1+1=2，

于是r(A)=2，即|A|=0=|0E-A|，λ3=0为A的特征值，方程组AX=0的基础解系应含有n-2个解向量，设其为γ3,γ4,…,γn，满足

Aγi=0=0γi(i=3,4,…,n)，

即γ3,γ4,…,γn为A的对应于特征值λ3=0的线性无关的特征值向量. 因此特征值λ3=0的重数为n-2，且α-β,α+β,γ3,γ4,…,γn线性无关，令矩阵P=(α-β,α+β,γ3,γ4,…,γn)，则P为n阶可逆矩阵，使

拓展 如果设矩阵B=kE+l(αβT+βαT)，E为n阶单位矩阵，k,l为任意非零实常数,αTα=βTβ=a>0，则同理可推得B可对角化，且

P为本例所求的可逆矩阵.

[参 考 文 献]

[1] 丘维声. 高等代数(上册)[M].北京:清华大学出版社，2013: 282-292.

[2] 陈维新,等. 线性代数学习指导和习题剖析[M]. 北京:科学出版社，2011: 120-140.

[3] 丘维声. 高等代数学习指导书(上册)[M].北京:清华大学出版社，2005: 332-343.

[4] 陈维新. 线性代数[M].2版. 北京:科学出版社，2007: 202-207.

[5] 胡金德,王飞燕. 线性代数辅导[M]. 3版.北京:清华大学出版社，2003: 336-371.

[6] 许甫华. 线性代数典型题精讲[M]. 3版.大连:大连理工大学出版社，2003: 237-278.