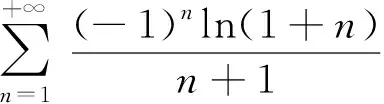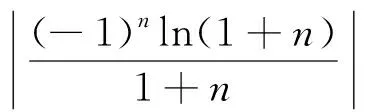对数函数与幂函数的序关系及其应用
宋明娟, 朱思宇
(黑龙江科技大学理学院,哈尔滨150022)
1 引 言
对数函数作为科学技术中的常用函数,经常出现在反常积分表达式和无穷级数的一般项中,要判定反常积分和无穷级数的敛散性目前有比较判别法、比较判别法的极限形式、阿贝尔判别法及狄利克雷判别法、对数判别法,比值判别法和拉贝判别法等[1-4]. 但最常用的方法还是比较审敛法,即将待判定函数与幂为-p的幂函数比较大小,视p与1的序关系来判定其敛散性,这就需要知道对数函数在不同的定义域内与何种幂函数有确定的序关系.到目前为止这种序关系还没有在文献及教材中查到,人们解决这类问题,还只能用试探的方式去寻找,这既影响了解题速度,也加大了解题难度.为此本文给出并证明了对数函数与幂函数的七种序关系.并应用这些序关系判别了6种被积函数中含有对数因子的反常积分的敛散性和1个一般项含有对数函数的无穷级数的敛散性.
实践表明,依据对数函数的定义域很容易就能在这些序关系中找到合适的幂函数做比较对象,从而能准确地为含有对数函数因子的反常积分或无穷级数的敛散性做出判断.
2 对数函数与幂函数的序关系
命题若0<λ≤e, 则对数函数与幂函数有以下序关系:
(i)λlnx≤x(x>0).

(iii) lnx≤x-1/λ(0 lnx≤x-2/5(0 (iv) ln(a-x)≤(a-x)-1/λ(0 (v) ln(1+x)≤x(x≥0). (vi) lnx≤x-1(x≥1). 证(i) 设f(x)=λlnx-x(x>0), 则有 显然x=λ是f(x)的唯一驻点且f″(x)<0,于是x=λ是f(x)的最大值点. 因为 当0<λ≤e时, 从而有 f(x)≤f(λ)≤0 (x>0). 即序关系 (i)λlnx≤x(x>0)成立. 令λ=2,λ=2.5,则分别有 取λ=2,λ=2.5,则分别有 lnx≤x-2/5(0 (iv) 当0 (vi) 当x≥1时,由序关系(v)有 lnx=ln(1+(x-1))≤x-1. 即序关系(vi)成立. 例1判别下列反常积分的敛散性 (5) 该瑕积分的瑕点为x=0和x=1. 因为 所以 (6) 该积分为无穷积分. 当x≥1时, [参 考 文 献] [1] 华东师范大学数学系.数学分析[M].4版.北京:高等教育出版社,2010. [2] 裴礼文. 数学分析的典型问题与方法[M].北京 高等教育出版社,1993. [3] 徐晶.一种反常积分和正项级数收敛的判别法[J].高等数学研究,2005,8(3):25—26. [4] 龙爱芳.两种反常积分敛散性的判别方法[J].大学数学,2012,28(4):140-143.
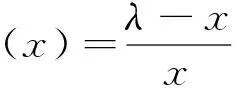
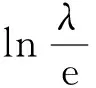
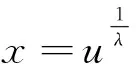




3 对数函数与幂函数的序关系在判别反常积分收敛性中的应用



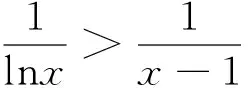
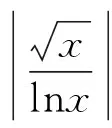
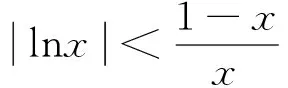
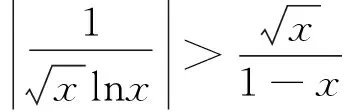
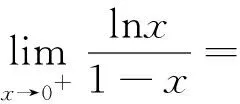
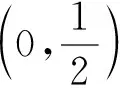
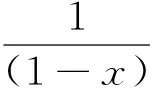
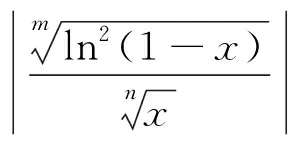
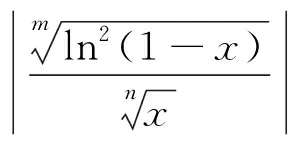
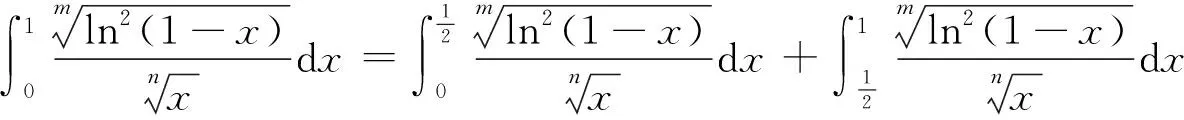
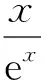

4 对数函数与幂函数的序关系在判别级数收敛性中的应用