实分析中关于Lipschitz条件的一个充要条件

林植林

(华南师范大学数学科学学院,广东广州510631)

在实分析中,Lipschitz条件和实函数往往会有着十分紧密的联系，例如有限实函数f(x)在[a,b]上满足Lipschitz条件的充要条件为f(x)是[a,b]上某个有界可积函数的不定积分[1].因此,对Lipschitz条件成立时充要条件的分析,对于研究实函数的某些性质则具有深远意义.

1 Lipschitz条件及相关引理

定义设f(x)是定义在[a,b]上的实函数.若存在一个常数M,使得对于∀x,y∈[a,b],都有f(x)-fy≤Mx-y成立,则称f(x)在[a,b]上满足Lipschitz条件.

引理1设f(x)为定义在[a,b]上的有限函数.若f(x)在每一点的导出数均为正数,则f(x)是[a,b]的严格增函数.

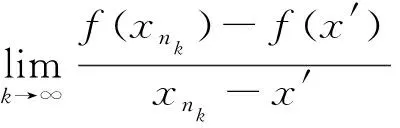
这表明f(x)在x′处有Dfx′≤0,与f(x)在每一点的导出数均为正数矛盾,故假设不成立,从而f(x)是[a,b]的严格增函数.

由引理1,可得到以下的引理2.

引理2设f(x)为定义在[a,b]上的有限函数.若f(x)在每一点的导出数均为非负数,则f(x)是[a,b]的增函数.

证取fμ(x)=f(x)+μx,其中μ>0,则有

Dfμ(x)=Df(x)+μ≥0+μ=μ>0.

由引理1可断言,fμ(x)在[a,b]上关于x严格单调递增.从而,当y>x,x,y∈[a,b]时,有

fy+μy=fμy>fμ(x)=f(x)+μx.

令μ→0+,可得

fy>f(x),

这表明f(x)为[a,b]的增函数.

2 Lipschitz条件成立的充要条件

定理f(x)在[a,b]上满足Lipschitz条件的充要条件是f(x)的所有导出数满足|Df(x)|≤M, ∀x∈[a,b].

证先证必要性.假定f(x)为在[a,b]上满足Lipschitz条件的实函数,则对于∀x1,x2∈[a,b],有

fx1-fx2≤Mx1-x2.

f(xn)-f(x0)≤Mxn-x0,

即

由x0的任意性知，f(x)的所有导出数满足Df(x)≤M.

下证充分性.先证f(x)为[a,b]上的连续函数.若不然,不妨设x′∈[a,b]为其不连续点,则存在ε0>0,存在αn→0n→∞,αn≠0,使得

fx′+αn-fx′≥ε0,

故有

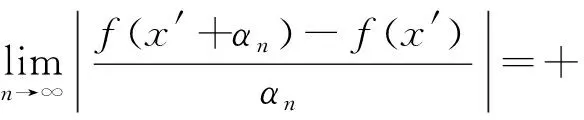
这与f(x)的所有导出数满足Df(x)≤M矛盾,故f(x)必为[a,b]上的连续函数.

现构造函数

g1(x)=Mx+f(x),g2(x)=Mx-f(x).

注意到Df(x)≤M,则有

Dg1(x)=M+Df(x)≥0,

Dg2(x)=M-Df(x)≥0.

由引理2知g1(x)与g2(x)均为[a,b]的增函数，故当x,y∈[a,b],且当y>x时,有

My+fy=g1y≥g1(x)=Mx+f(x),

My-fy=g2y≥g2(x)=Mx-f(x),

从而有

-My-x≤fy-f(x)≤My-x,

即

f(x)-fy≤Mx-y.

这表明f(x)在[a,b]上满足Lipschitz条件.

[参 考 文 献]

[1] 程其襄,等.实变函数与泛函分析基础[M].北京:高等教育出版社,2003:97-175.

[2] 周民强.实变函数论[M].北京:北京大学出版社,2001:149-270.

[3] 曹广福.实变函数论与泛函分析(上册)[M].3版 .北京:高等教育出版社,2011:96-139.

[4] Aliprantis C D.Principles of real analysis[M].北京:世界图书出版公司,2008:161-254.