答非所问的速度改变辨析

，

(1.天津渤海职业技术学院，天津 300221；2.天津商务职业学院，天津 300221)

一、 关于加速与减速

需要明确的是：加速(等价速率|v|变大)还是减速(等价速率|v|变小)是对速率|v|改变而言，而非对速度v改变而言。下面以较熟悉的竖直上抛物体的运动来说明之。

以初速度v0竖直上抛物体的运动速度公式为v(t)=v0-gt(1)

实际上需考虑方向，即考虑上升(正方向)与下降(反方向)两种情形：

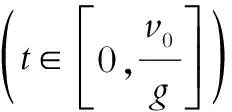
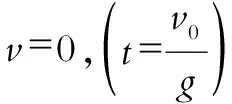
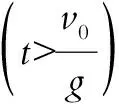
v逐渐减小的事实可以用初等数学方法说明：直线v(t)=v0-gt的斜率-g<0，说明物体运动速度单调v减少；

v逐渐减小的事实还可以用高等数学方法进一步证实：由(1)式求导得v′(t)=-g<0，套用函数单调性判定定理，说明物体运动速度v单调减少。

v逐渐减小的事实见图1即可一目了然。

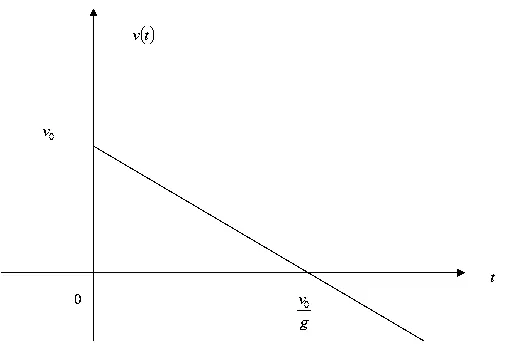
图1 竖直上抛运动速度图

二、 例的答案为答非所问

下面例及解均是[1]书在77-78页上的例4及解[1]。

解 由于故当时v′(t)=3t3-21t2+30t=3t(t-2)(t-5)，故当02时，v′(t)>0，即运动是加速的；当20，即运动又是加速的。

当一中明确加速还是减速是对速率|v|的改变而言后，自然而然地会知道，例问的问题是运动速度v的改变情况怎样，而例给出的答案是运动速率|v|的改变情况怎样，故例的答案为答非所问。

三、 例的答案为答为所问(运动速度的改变情况)的判定研究

由于例未弄清加速还是减速是对速率|v|改变而言，而非对速度v改变而言，即对速率改变与速度改变未区分好，导致答案为答非所问，故需要修改例的答案。

根据函数单调性的判定定理，我们可以直接v′(t)用符号研究v的单调性，即当00，说明运动速度v单调增加；当20，说明运动速度v又单调增加。

四、 运动速率的改变情况的判定研究

虽然三中借助函数单调性判定定理，澄清用v′(t)的符号判定的是速度改变，而非判定速率改变，但未解决速率改变判定的问题。下面进一步解决如何用构造τ′(t)(τ=|v|)的的符号判定速率改变的问题。

受竖直上抛运动的启发，上升时，τ>0(τ=|v|)，用τ′的符号研究τ=|v|加速还是减速正确；下降时，v=0，取τ=-(v0-gt)(τ=|v|)，再用τ′的符号研究τ=|v|加速还是减速也正确，见图2。

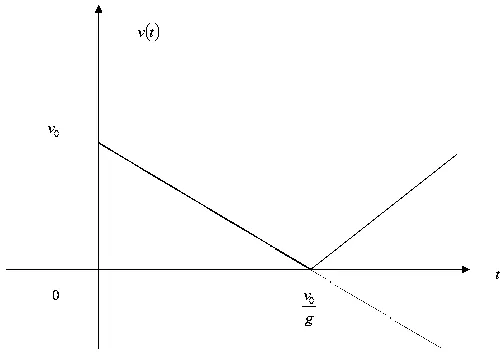
图2 竖直上抛运动速率图

一般地，用v(t)=0的时间t把整个时间分成若干部分，在每个部分区间上v(t)>0或v(t)<0。与函数单调性判定定理的用法类似：

当v(t)>0时，用τ′的符号研究τ=|v|加速还是减速；

当v(t)<0时，用τ′的符号研究τ=|v|加速还是减速。

五、有意思的加、减速与数学中关于正(或负)号美

最后需要进一步澄清：加速可能是速度单增，如正方向上的速度变大，还可能是速度单减，如图1的下降过程；同样，减速可能是速度单增，如反方向上的刹车过程，还可能是速度单减，如图1的上升过程。关键问题是，“+”号表示“正方向”，“-”号表示“反方向”，在此也可以体会到数学中关于正(或负)号美。

参考文献：

[1]上海师范大学数学系，中山大学力学系，上海师范学院数学系合编. 高等数学[M].北京：高等教育出版社，1991.