基于遗传算法的控制分配在飞艇中的应用
贾瑞, 吴梅
(西北工业大学 自动化学院, 陕西 西安 710129)
0 引言
飞艇在低速飞行或定点盘旋时,舵面效率不足会导致操纵性能下降;因此单一执行机构的控制已无法满足需求,利用推力矢量和舵面进行复合控制是一种有效的方式。复合控制中同时参与控制的执行机构不是唯一的,合理分配操纵指令以满足性能需求,就需要研究控制分配问题。对比现有的控制分配方法,非线性规划中带约束条件的二次规划能够很好地描述控制分配问题[1],物理意义直观明显,且更加贴近实际;但是传统的二次规划解法比较复杂且效率低,很难达到实时应用的目的。遗传算法具有覆盖面大和全局寻优等诸多优点,所以在处理非线性规划等问题方面有很大的潜质。
本文提出了将遗传算法和二次规划相结合的思路,将控制分配问题数学化为约束二次规划问题,然后对飞艇纵向的控制分配问题采用遗传算法进行求解,最后仿真验证了该方法的可行性。
1 推力矢量模型
推力矢量能增加飞艇的控制余度,在飞艇起降、定点等特殊飞行状态下,对改善飞艇的机动性能有巨大作用。本文研究的飞艇安装两台涵道式螺旋桨发动机,位于吊舱下方、左右对称分布,带推力矢量飞艇侧视图如图1所示。图中,δe为升降舵角;δTL为推力矢量偏角。
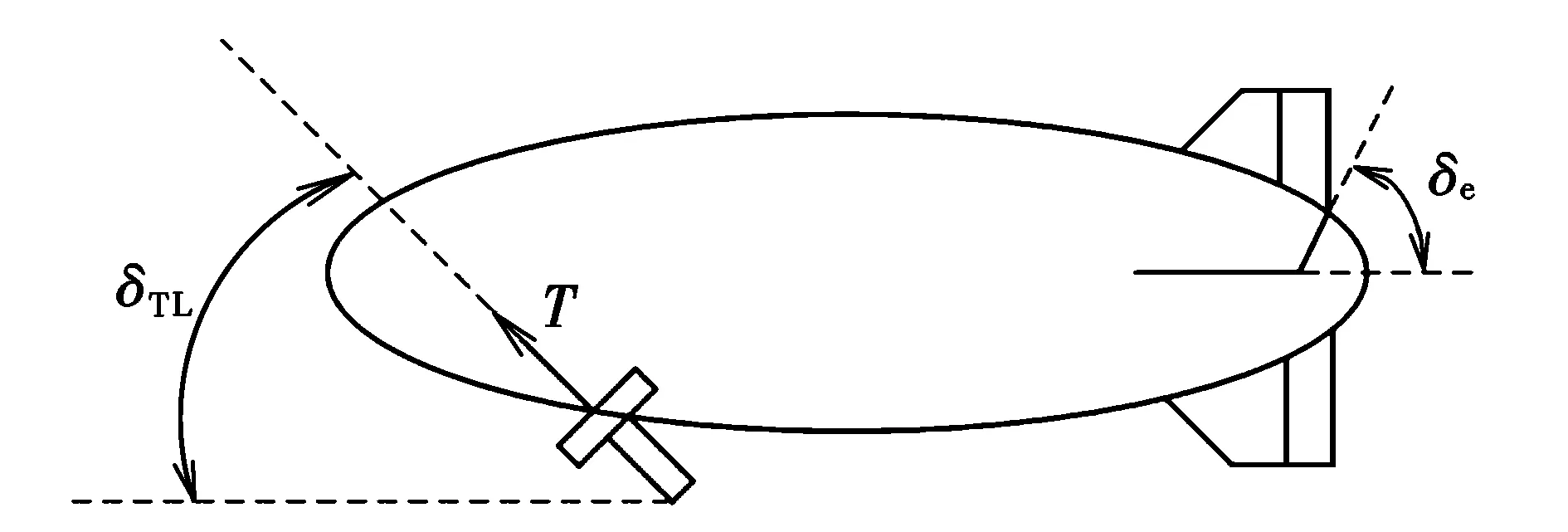
图1 推力矢量飞艇Fig.1 Airship with thrust vector
图2描述了推力矢量的原理,坐标系Oxyz为飞艇艇体坐标系。
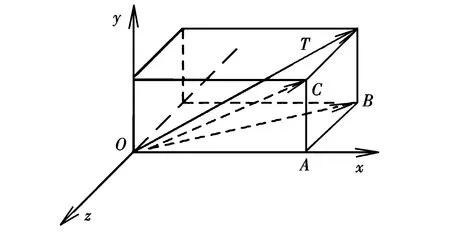
图2 推力矢量原理图Fig.2 Thrust vector schematic diagram
假设某时刻发动机偏转角度在图中T位置,经过投影可以求得发动机推力在飞艇艇体坐标系下的分量表达式为:
(1)
式中,δy,δz对应图2中∠AOB和∠AOC。设推力作用线到飞艇体积中心的矢径为:
(2)
则单台发动机的推力产生的力矩为:
M=R×T
(3)
为了方便控制,两台推力发动机同时偏转。本文研究飞艇纵向的控制分配问题,所以只考虑推力发动机上下偏转的情况。
2 控制分配问题
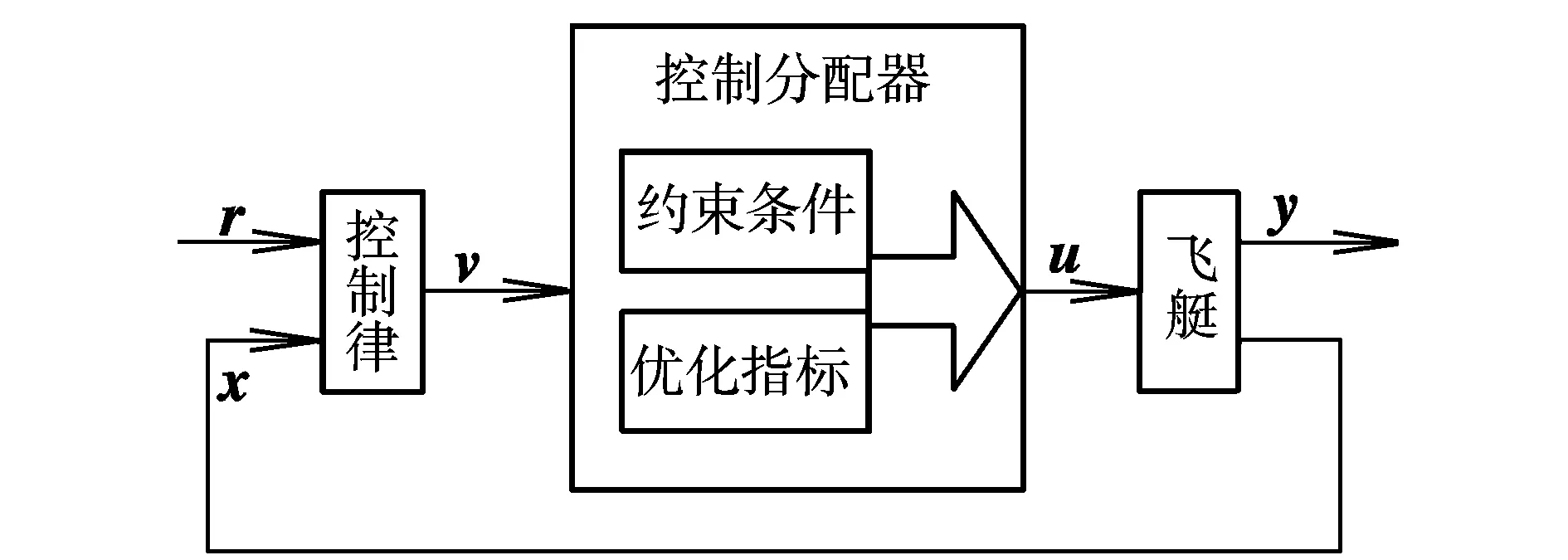
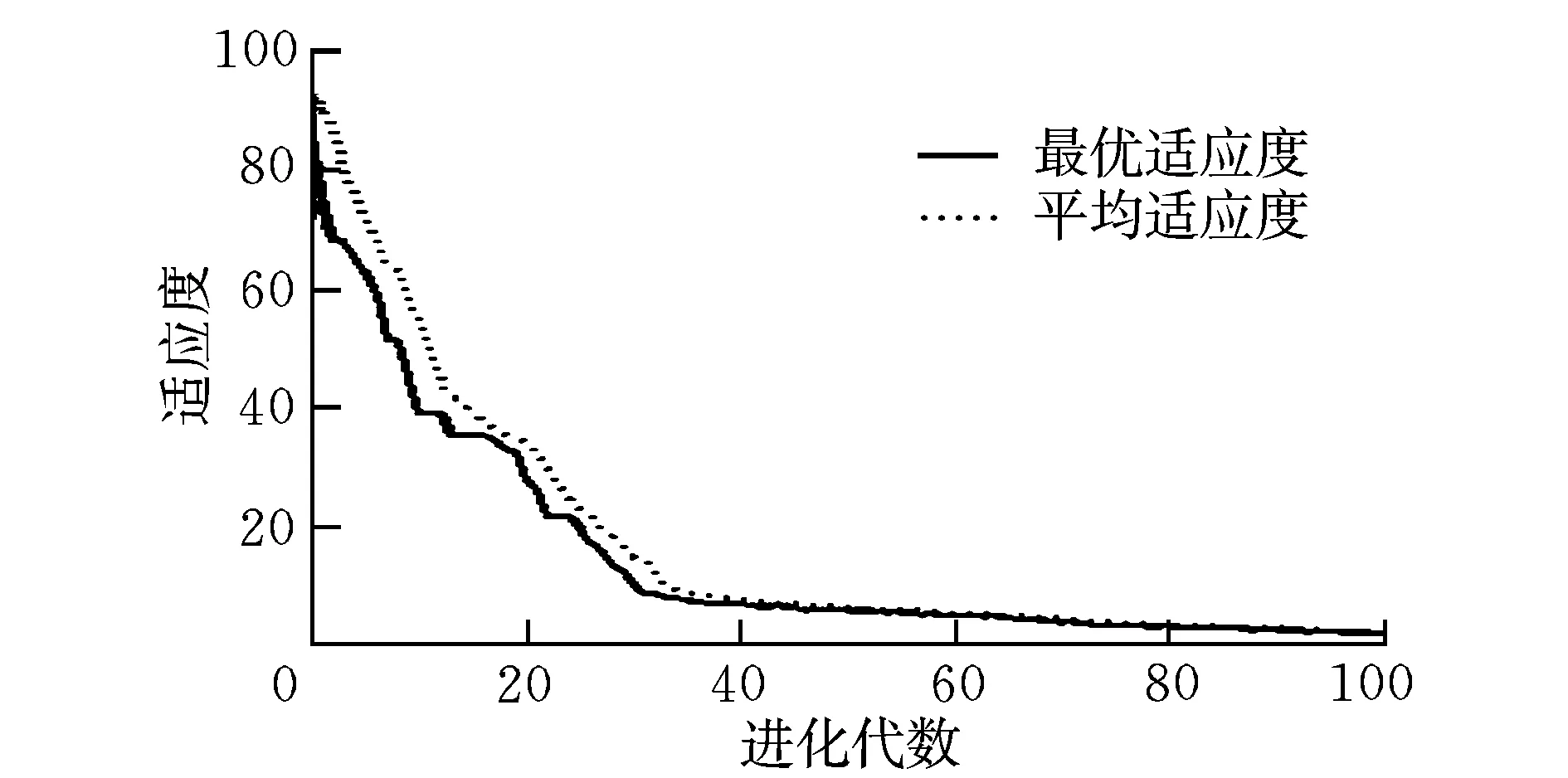
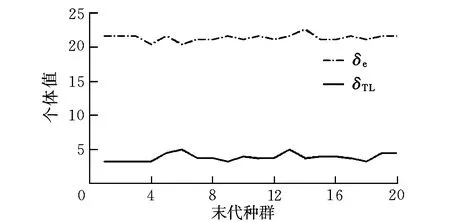
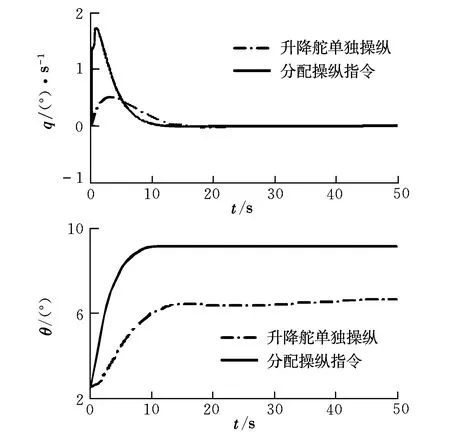
在飞行控制中,控制分配的目的是通过一定的规则给不同的执行机构分配操纵指令,产生期望的滚转、俯仰或偏航力矩。假定通过控制律解算出的期望力矩v(t)∈Rm,执行机构的偏转量u(t)∈Rn,其中m Bu(t)=v(t) (4) 式中,B∈Rn×m为控制效率矩阵。 执行机构位置和速度的约束表示如下: (5) (6) 综合式(5)、式(6),单个采样周期内的执行机构约束可写为: u1(t)≤u(t)≤u2(t) (7) 式(7)左右两端的变量可通过下式求得[3]: (8) 所以,带约束条件的控制分配问题的数学模型可以描述为如下标准形式: {Bu(t)=v(t)|u1(t)≤u(t)≤u2(t)} (9) 实际期望的力矩v(t)不一定是可达的,即便可达,其解也不一定唯一。如果解不唯一,另一个目的是对控制输入产生的代价进行优化。结合以上两点,采用混合优化指标[4],将控制分配问题描述为约束二次规划问题的优化指标函数为: 传统的教学模式是老师教、学生学,但老师教的如何、学生掌握的如何,以及学生对各项运动项目的掌握已经达到什么等级,没有一个客观的评价标准。《标准》的出台,有效解决了如何评价体育运动技能掌握情况,一是让政策落地实施,找到了可靠的抓手,进而使政策发挥出效力;二是打破了理论与实际之间的界限,以政策为指导,使实践焕发无限活力! (10) 式中,‖·‖2为二范数;φ(u)为执行机构偏转的代价函数。当推力发动机偏转后需要增加推力来保持原来的速度,因此必须考虑推力矢量的能耗。通过选择混合优化指标,兼顾了力矩误差和输入能耗,其中λ为权值,用于调整在优化时先满足哪个目标,λ一般取较小值。引入控制分配后飞艇的飞行控制律框图如图3所示。 图3 带控制分配器的飞行控制Fig.3 Flight control with control allocator 本文采用遗传算法寻找满足执行机构约束的控制输入。控制分配的目的是求解满足期望指标J的多个执行机构的输入,即: J=f(u1,u2,L,un) (11) 因此,控制分配问题的解是不同执行机构的输入,采用有利于处理优化问题的实数编码表示个体,将多个执行机构的输入表示为遗传个体x=[x1,x2,…,xn]。 具体操作步骤为: (1)初始化。初始化就是确定执行机构输入组合的个数,即种群规模N以及交叉和变异的概率Pc和Pm,最后确定终止种群进化的规则。本文指定种群进化到100代时终止。 (2)个体选择[5]。个体选择采用比例选择方式。设个体适应度为fi,则个体被选择的概率为: (12) (3)种群进化。种群的进化是通过交叉和变异操作来完成的,通过交叉和变异可以产生新的个体。交叉是随机选择两个用于繁殖下一代的不同个体的相同基因位置,按交叉概率Pc在选中的位置进行交换。变异是对个体的某些基因位置按变异概率Pm执行异向转化。 对于带推力矢量操纵机构的飞艇,推力发动机的偏转使得推力在速度方向的分量大幅变化,对飞艇速度产生较大影响,因此对飞艇设计速度保持控制律至关重要。本文采用PID方法设计了飞艇速度保持控制律,其原理框图如图4所示。 图4 速度保持原理Fig.4 Speed keep principle 控制律表达式为: (13) 由于飞艇推力矢量控制具有明显的非线性,所以采用飞艇的非线性模型进行仿真,只考虑纵向,飞艇初始状态为水平平飞,状态参数为:H=3 000 m,V=20 m/s;纵向的控制输入为u=[δe,δTL]T。在该飞行状态下,执行机构的约束和效率特性见表1。 仿真中飞艇跟踪俯仰角θg=10°的给定值。首先根据俯仰跟踪指令解算出期望力矩v(t),连同表1的已知数据对分配指标和式(5)的相应变量进行赋值;然后采用遗传寻优方法寻找满足约束条件和使得代价函数最小的控制输入。 为了提高遗传算法效率,并且防止遗传算法早熟而进入局部收敛,经过反复试验,选择种群规模N=20,交叉概率Pc=0.7,变异概率Pm=0.25,对推力发动机偏转产生的代价加以考虑,选择权值λ=0.05,得到遗传算法寻优进程如图5所示。 图5 遗传算法进程Fig.5 Process of genetic algorithm 从图5适应度的收敛情况可以看出,实际优化进程在种群进化到40代左右时已经找到并收敛到最优值。 末代种群个体值见图6。可以看出,末代种群的所有个体值已经收敛,达到了较平稳的状态,收敛结果为[21.725,3.706 3]。 图6 末代种群个体值Fig.6 Individual value of the last population 用分配结果对飞艇的俯仰跟踪进行复合控制,并得到俯仰角速度、俯仰角的变化曲线,与单独采用升降舵操纵时相应参数的变化曲线进行对比的结果如图7所示。 由图7仿真结果可以看出,升降舵单独操纵时,50 s时θ<7°,这是由于速度较低时升降舵的效率大幅下降造成的。控制分配后纵向的操纵性能明显提升,θ在10 s左右时已超过8°,但是终值并未达到10°,因为在代价函数中,兼顾了推力发动机偏转的代价,没有优化到使Bu和Vd严格相等。如果对实现期望指令的需求比较严格,可以置λ=0,不考虑推力发动机的能耗。综上所述,控制分配取得了较好的效果。 图7 仿真结果Fig.7 Simulation results 本文建立了控制分配问题的约束二次规划模型,然后利用遗传算法进行寻优求解。遗传算法有效地解决了约束二次规划的求解问题,给出了合理的控制分配方案,为控制分配问题提供了新的解决思路。该方法也可以在舵面故障等条件下,通过更改约束条件和控制效率矩阵实现重构。 参考文献: [1] 马建军,李文强,李鹏,等.飞行器控制分配技术研究现状与展望[J].飞行力学,2009,27(3):1-5. [2] 占正勇,刘林.控制分配在复杂飞行控制系统中的应用设计[J].飞行力学,2006,24(2):73-76. [3] 陈怀民,徐奎,马松辉,等.控制分配技术在无尾飞机纵向控制系统中的应用研究[J].西北工业大学学报,2007,25(2):199-203. [4] Petersen J A M,Bodson M.Constrained quadratic programming techniques for control allocation [J].Control Systems Technology, IEEE Transactions on,2006,14(1):91-98. [5] 何光宇,周军,呼卫军.基于遗传算法的多执行机构控制分配策略[J].西北工业大学学报,2010,28(1):23-26.
3 控制分配算法
4 速度保持模块

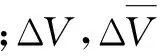
5 仿真及结果分析
6 结束语

