基于物理的波浪实时模拟方法

张志毅，吕之华

(西北农林科技大学信息工程学院，陕西 杨凌 712100)

基于物理的波浪实时模拟方法

张志毅，吕之华

(西北农林科技大学信息工程学院，陕西 杨凌 712100)

为解决广域范围内波浪状态的实时计算和可视化问题，结合无粘滞流体力学的物理模型，提出了一种以三角形为控制单元的有限体积简化算法。该算法的优点在于：以不规则边界区域的非规则三角网格为基础，通过简化通量向量分裂方法获得三角形控制单元的边界数值通量，能快速逼近二维浅水方程的解进而模拟非规则边界浅水的实时流动。实验结果显示，所提方法能在符合现实世界物理规律的前提下较好地实现大规模波浪的实时可视化模拟。

浅水方程;限定Delaunay三角剖分;有限体积法;通量向量分裂法

1 引言

水以其在自然与社会中的不可或缺及其本身所拥有的丰富特性和行为，一直以来都是人们的重点研究对象。近年来，因实时水流仿真在现实应用中的迫切需求，已吸引了众多学者对其展开相关研究。Navier-Stokes方程是描述流体运动的基本方程，但其数学表达和求解复杂且困难，在通常情况下甚至不可能求得解析解。当求其数值解时，常因所选择的方法导致耗时极长。对于海啸模拟演化、洪水破坏预测、计算机动画等实时性较强的应用程序来说，模拟水流需要极快的速度。严格来说，水的流动是三维的，但为满足快速计算的需要可将其降为二维问题，即将水体看成在某一个平面上的高度域，并使用“浅水”[1]条件简化Navier-Stokes方程获得双曲型偏微分方程组，用于描述水流的表面信息。对满足“浅水”条件的流体，可通过计算流体力学方法求得浅水方程的数值解。主要方法有三种：有限差分法、有限元法和有限体积法。有限差分法FDM(Finite Difference Method)[2]简单易于理解，速度快，但精度不高。有限元法FEM(Finite Element Method)常用于固体力学，用于流体力学方面还有待改善。有限体积法FVM(Finite Volume Method)[3～5]的基本思路是将计算区域划分为一系列不重复的控制体，并使每个网格点周围有一个控制体，将待解的微分方程对每一个控制体积分，得出一组离散方程。使用FVM是对推导原始微分方程所用控制体途径的回归，其数值逼近的物理意义更直接明晰。

综上所述，FVM能像FEM一样适用于任意不规则网格，着眼于控制体上的逼近，具有守恒性，其处理效率与FDM相近，远高于FEM。也就是说，FVM集FEM的几何灵活性和FDM的高效率于一体，因此常用于解决流体方面的问题。

2 有限体积法解浅水方程

浅水方程[6,7]的守恒形式可表示为：

(1)

其中，

式中，h是水深，u是x方向的速度，v是y方向的速度，g是重力加速度。B(U)是源项。浅水方程是一个非线性偏微分方程组，得不到解析解，需数值方法求解。本文使用有限体积法解浅水方程。

2.1 控制体的选择与生成

使用有限体积法时，需先选择适合的控制体作为计算区域中的最小单元[8]。本文选择三角形作为基本控制体。对于非规则边界的区域，通常可用限定Delaunay 三角剖分CDT(Constrained Delaunay Triangulation)方法[9～11]来生成高质量的非规则网格。

为实现数值离散方法[12～14]和通量向量分裂方法的快速精确求解，通常有两种方法来选择控制体： 格子中心式CC(Cell-Centered)和格子顶点式VC(Vertex-Centered)。以三角形网格为例来表达这两种格式的区别是：CC 的每一个控制体是一个三角形，三角形中各物理量被认为是常数；VC 的每一个控制体是以某一顶点为中心，以其周围的三角形的形心/外心连线为边界构成的多边形。本文选用三角形的CC作为控制体。

2.2 数值离散

当选用格子中心式的三角形为基本控制体时，如图1所示，n是边的法向量，θ是n与x轴的夹角。对式(1)积分，可得式(2)。

Figure 1 Schematic diagram of control unit图1 控制单元示意图

(2)

每个控制体单元中的U以常数近似，即当U的值均相同时，左端第一项可表示为：

(3)

其中，A是控制体的面积。

对于式(2)中左端第二项，由格林公式可得：

(4)

式(2)右端可表达为：

(5)

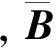
(6)

对于时间项，采用前向差分格式：

(7)

对于式(6)的左端第二项，若令：

E=Fcosθ+Gsinθ

(8)

则(6)式的左端第二项可表示为：

(9)

将式(7)和式(9)代入式(6)，可得到式(10)和式(11)：

(10)

(11)

因欧拉方程具有旋转不变性[15]，而浅水方程的数学形式和欧拉方程是相同的，于是有：

F(U)cosθ+G(U)sinθ=T(θ)-1F(T(θ)U)

(12)

其中，

(13)

由式(12)和式(13)可得：

(14)

其中，

(15)

则式(11)可化为式(16)：

(16)

2.3 通量向量分裂法解黎曼问题

当水流在空间或时间域产生不连续变化时，凡在单元交界面上发生的下述现象均属于黎曼问题：由初始间断的左右状态，确定t>0时的波态、波强度及波间的流动特性的问题。黎曼问题是解决不连续物理问题的数学描述方程，是设计高解析度数值方法的核心。其微分方程形式为双曲守恒律方程组：

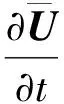
(17)

其初值条件为：

(18)

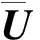
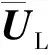
(19)

其中J是雅克比矩阵。J可以表示为：

J=PΛP-1

(20)

其中Λ=diag(λi)，P是J的右特征向量构成的矩阵。根据λi的符号不同，J可表示为：

J=PΛP-1=P(Λ++Λ-)P-1=J++J-

(21)

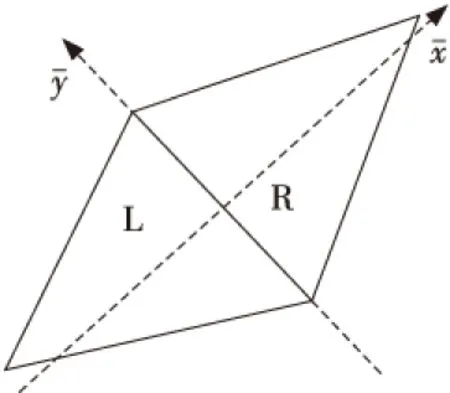
Figure 2 Schematic diagram of Riemann problem图2 黎曼问题示意图

由式(19)～式(21)可得：

(22)

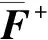
(23)

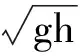
(24)

其中，

(25)

(26)

通过式(16)、式(26)和给出的边界条件，即可求解浅水方程。

2.4 边界条件

水域的边界分为两种情况：开边界和闭边界。如图2所示，对于边界情况，L是存在的，R是不存在的。现假设一个虚拟的R，然后给它赋值。

对于开边界，法向的值可表示为：

(27)

对于闭边界，法向的值可表示为：

(28)

基于上述理论，水面的高低变化可精确计算。尚存在的问题如图3所示：C1至C5的高度能计算，但V点的高度不能。这是因为选取的控制体为三角形，而V并不是属于某一个控制体内的物理量。然而为了模拟水流的边界情况，V点是必需的。考虑到剖分结果中的三角形都趋近于正三角形，当其尺寸很小时，V点高度可近似用式(29)计算。

(29)

其中，n是V点周围三角形的数量。当三角形尺寸很小时，用平均法计算V点高度，对于建立实时水流动画来说，可以取得速度和精度的平衡。

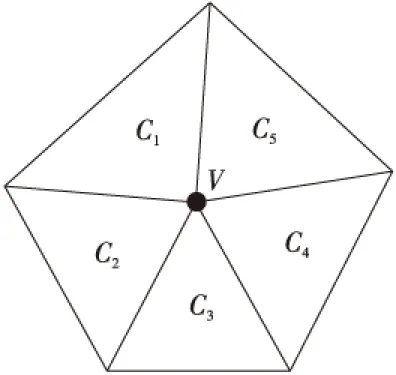
Figure 3 Obtain the water height in point V图3 获取V点的水高

3 实验结果

实验结果如图4和图5所示。本实验程序在Visual Studio 2010下开发，图形库使用OpenGL。程序运行于Intel Pentium(R) Dual-Core CPU T4300，2.10 GHz，内存为2 GB，显卡为NVIDIA GeForce G210M。

图4显示对一组真实地形数据进行三角剖分的结果。该数据来源于陕西省某天然湖面的边界线，湖面长约4.8 km，宽约2.8 km，非规则边界线约长17.2 km，原始数据为精度50 m的DEM数据。图4a中每个三角形外接圆半径都小于14 m。图4b中每个三角形外接圆半径都小于7 m。结果显示，本三角剖分算法效果良好，且易于控制三角形尺寸和质量。在实际使用中，三角形尺寸要根据情况选定，考虑到精度，建议外接圆半径小于3 m。

图5显示如图4所示地形的模拟结果。图5中，三角形外接圆半径取为1 m，三角剖分产生的三角形为56 046个，运行时状态间的时间间隔为Δt=30 ms，即每秒可实现至少33帧精细图像，达到了实时模拟计算。图5a～图5d分别为激波后2 280 ms、5 460 ms、7 950 ms和12 810 ms时刻湖面状态的模拟结果。因地形中有“湾”存在，数值计算结果和可视化结果均显示：当水流进入“湾”后，因流量固定，受地形挤压，其水面高度会高于宽阔“湖面”上的波高，且水流速度也较快。这真实地反映了波浪运动遵循伯努利流体方程的实际情况。

Figure 4 Triangulation results of a real terrain boundary region图4 真实地形边界区域的三角剖分结果

Figure 5 Wave simulation results corresponding to Figure 4 terrain图5 对应于图4中地形的波浪模拟结果

表1显示了本方法与其它三种方法耗时对比结果。比较时所用的数据均为如图4所示的相同数据，所生成的图像分辨率均为1 024×768像素。其中差分逼近法是采用文献[17]的方法实现；余弦波叠加法采用文献[18]的方法实现；Perlin 噪声法是采用文献[19]的方法实现。本文所用方法和差分逼近法及余弦波叠加法均是以物理模型为基础的仿真计算，而Perlin噪声法仅是为满足视觉效果而做的虚拟现实处理。从实验结果可以看出，本文所提的方法能真正满足较大水域内波浪的实时模拟。

Table 1 Time-consuming comparison among the present method and other methods

因本文所提方法简化了流体内部的摩擦损耗，模拟结果与实际水流波浪相比较，运动速度略快，且在波的干涉现象表现上尚有不足。

4 结束语

本文提供了一种模拟非规则边界水流运动的方法。简单来说分为两部分：三角剖分和浅水方程的数值计算。为获得良好的计算区域，本文使用了高效的限定Delaunay三角剖分算法，并进行尺寸控制和质量控制，使得三角剖分足够密且更趋近于正三角形。接着使用有限体积法解偏微分方程，为了解决控制体边界上的数值通量问题，使用了通量向量分裂法(FVS)。实验结果表明，本方法简单稳定且速度很快，能满足实时性要求。

本文主要侧重于水流模拟的理论研究，因此在水流的渲染上还有待提高。此后的工作重点是水流的渲染，主要包括粒子生成和光照影响。

[1] Tan Wei-yan. Computational shallow water hydrodynamics—the application of the finite volume method[M]. Beijing:Tsinghua University Press, 1998.(in Chinese)

[2] Causon D M, Mingham C G. Introductory finite difference methods for PDEs[EB/OL].[2010-05-16]. http://bookboon.methods-for-pdes-ebook.

[3] Li Ren-xian.The basis of finite volume method[M]. Beijing:National Defence Industry Press, 2008.(in Chinese)

[4] Versyeeg H K,Malalasekera W.An introduction to computational fluid dynamics[M]. England:Longman Group Ltd, 1995.

[5] Bowyer A. Computing dirichlet tessellations[J]. The Computer Journal, 1980,24(2):162-166.

[6] Chippada S, Dawson C N，Martinet M L, et al. Compute methods appL[J]. Mech Eng，1998,151(1-2):105-129.

[7] Rogers B M, Fujihara M, Borthwick A G L. Adaptive Q-tree Godunov-type scheme for shadow water equation[J]. International Journal for Numerical Methods in Fluids, 2001, 35(3):247-280.

[8] Pan C, Dai S, Chen S. Numerical simulation for 2D shallow water equations by using Godunov-type scheme with unstructured mesh[J]. Journal of Hydrodynamics, 2005,18(4):475-480.

[9] Yang Qin. Constrained Delaunay triangulation mesh generation technology[M]. Beijing:Publishing House of Electronics Industry, 2005.(in Chinese)

[10] Du Min. Unstructured triangulation grid generation and its application in 2D hydrodynamics model[D]. Tianjin:Tianjin University, 2005.(in Chinese)

[11] Zhang Zhi-yi, Konno K, Tokuyama Y. Curve mesh reconstruction based on mountain contours [J]. Journal of the Institute of Image Information and Television Engineers, 2006, 60(11):1803-1810.

[12] Zhao Di-hua, Yao Qi, Jiang Yan, et al. FVS scheme in 2D depth-averaged flow-pollutants modeling[J]. Advances In Water Science, 2002, 13(6):701-705.(in Chinese)

[13] Zhang Li-qiong,Cui Guang-bai,Yang Jue.Flux vector splitting and finite volume method in the application of hydraulic modeling[J]. Water Resources and Hydropower Engineering, 2001,8(32):8-11.(in Chinese)

[14] Roshandel A,Hedayat N,Kiamanesh H.Simulation of dam break using finite volume method[J]. World Academy of Science, Engineering and Technology, 2010,48(4):112-115.

[15] Spekerijse S P. Second order accurate upwind solutions of the 2D steady Euler equations by the use of a defect correction method[C]∥Proc of the 2nd European Conference on Multigrid Method, 1986:285-300.

[16] Steger J L, Warming R. Flux vector splitting of the inviscid gasdynamic equations with application to finite difference methods[J]. Journal of Computational Physics, 1981, 40(2):263-293.

[17] Pang Ming-yong. The real time dynamic simulation method of two dimensional water waves based on the discrete model[J]. Shuili Xuebao, 2007,38(11):1358-1363.(in Chinese)

[18] Gao Zhi-yi, Yu Fu-jiang, Xu Fu-xiang. Preparing 3-D animation of sea wave forecasting[J]. Marine Science Bulletin, 2011,30(2):173-178.(in Chinese)

[19] Li Yun-fei,Cheng Tian-tian,He Wei.Simulation method for lake surface wave[J]. Journal of System Simulation,2009,21(23):7507-7510.(in Chinese)

附中文参考文献：

[1] 谭维炎. 计算浅水动力学—有限体积法的应用[M]．北京：清华大学出版社, 1998.

[3] 李人宪. 有限体积法基础 [M]. 北京：国防工业出版社, 2008.

[9] 杨钦. 限定Delaunay三角网格剖分技术[M]. 北京：电子工业出版社,2005.

[10] 杜敏. 非结构三角网格生成及其在二维水动力学模型中的应用[D]. 天津：天津大学, 2005.

[12] 赵棣华, 姚琪, 蒋艳, 等. 通量向量分裂格式的二维水流-水质模拟 [J]. 水科学进展, 2002, 13(6):701-705.

[13] 张丽琼, 崔广柏, 杨珏. 通量向量分裂格式及有限体积法在水流模拟中的应用 [J]. 水利水电技术,2001,8(32):8-11.

[17] 庞明勇. 基于离散模型的二维水波实时动态模拟方法 [J]. 水利学报, 2007,38(11):1358-1363.

[18] 高志一，于福江，许富祥. 海浪预报三维动画计算原理与制作方法 [J]. 海洋通报, 2011,30(2):173-178.

[19] 李云飞，程甜甜，何伟. 一种湖面波浪模拟的方法 [J]. 系统仿真学报, 2009,21(23):7507-7510.

ZHANG Zhi-yi,born in 1974,PhD,associate professor,his research interest includes computer graphics.

A method of real time wave simulation based on physical

ZHANG Zhi-yi,LÜ Zhi-hua
(College of Information Engineering,Northwest A&F University,Yangling 712100,China)

In order to solve the real-time computation and visualization of the wave state in the wide area, by combining the physical model of non-viscous fluid dynamics, a simplified finite volume algorithm is proposed, which uses triangle as control unit. The advantage of the proposed algorithm is that: Based on irregular triangular mesh of irregular boundary area, the boundaries' numerical flux of triangles can be obtained by simplifying flux-vector splitting method. Then shallow water flow with irregular boundary can be real-time simulated by fast approaching the solution of the two-dimensional shallow water equations. Experimental results show that the real-time visual simulation of the wave can be better achieved by using this method in the physical laws of the real world under the premise.

shallow water equations;constrained Delaunay triangulation;finite volume method;flux-vector splitting method

2012-09-20;

2012-12-19

教育部留学回国人员科研启动基金资助项目(K314020901)；中央高校基本科研业务费专项基金资助项目(Z109021004)

1007-130X(2014)03-0508-05

TP391.41

A

10.3969/j.issn.1007-130X.2014.03.023

张志毅(1974-),男,山西夏县人，博士，副教授，研究方向为计算机图形学。E-mail:815802490@qq.com

通信地址：712100 陕西省杨凌市西农路22号西北农林科技大学信息工程学院

Address:College of Information Engineering,Northwest A&F University,22 Xinong Rd,Yangling 712100,Shaanxi,P.R.China