一种求解最小双费用流问题的算法

马宇斌，谢 政，陈 挚

(国防科学技术大学理学院，湖南 长沙 410073)

一种求解最小双费用流问题的算法

马宇斌，谢 政，陈 挚

(国防科学技术大学理学院，湖南 长沙 410073)

多目标优化是网络最优化的一个重要子问题。通过实际应用案例，抽象出一种带容量限制的双费用权网络模型，并由此提出了相应的最小双费用流问题。之后，借鉴网络分层的思想，根据双费用权网络的特点设计出一个求解该问题的双层原始对偶算法，并严谨地证明了算法的正确性，估计出算法的复杂度为O(n2v0)。此外，对算法进行了推广改进，使其能求解一般k费用权网络中的最小k费用流问题。最后，通过一个实例来演示算法的执行。

双费用权网络；最小双费用流；双层原始对偶算法；复杂度

1 引言

网络多目标优化问题作为组合最优化和网络图论的一个交叉问题，一直以来在工程规划、地理信息系统、通信网络和交通运输等领域有着十分广泛的应用。尤其是近年来，随着通信和航天技术的发展，各国都在大力研发天基信息网络系统，以争取在海、陆、空、天等领域取得自主控制权；而对天基信息网络的研究归根到底就是求解一个多权网络最优化问题，其求解目标会因研究侧重点或分析方法的不同而不同。若将网络链路上的信息通行代价和丢包率这两个重要参数看成是特殊的“费用”，再辅以链路带宽约束，则问题就变成一个带容量限制的双费用权问题。对于双费用权问题，传统的网络流算法[1～4]已经不再奏效。王焕雄等[5]从不同角度讨论了含有弧容量和弧费用的双权有向网络，给出了计算两个节点间的使费用与容量之比最小的路径的多项式算法，但这种“双权”包括了容量，实质仍是单费用网络；Zhu De-tong[6]针对广义多品种最小费用流问题，提出一种对偶理论，将问题转化成一对含有内、外层问题的双水平规划，并导出相应的Kuhn-Tucker条件，但未给出具体算法及复杂性分析；孙小军等[7]提出了单费用运输网络中的最少时间最小费用路问题，即要求找出通行时间最短的最小费用路，并给出了一个求解算法；Coello[8]于2006年针对双目标综合优化问题提出了基于计算效率的进化算法，使运算时间大幅下降，但在理论上无法保证算法收敛；敖友云等[9]对综合优化问题提出了一种差分进化算法，通过引进Paretoε-支配关系来控制进化策略和参数范围，提高了求解的成功率；吴润秀[10]对双权网络最优化求解提出一种基于粒计算的分层算法，通过将双权复杂网络映射成一个分层网络，得到数据分布优化的满意解。

本文在对带容量限制的网络双费用权问题进行分析和探讨的基础上，结合文献[6]和原始对偶算法的思想，针对双费用权分主次的情况，提出了一种能有效求解此类最小双费用流问题的算法。

2 数学模型建立

对于天基信息网络，如果把卫星抽象成节点，把星际链路抽象成有向弧，将信息通行代价记为主单位费用w1，将丢包率记为次单位费用w2，那么该实际问题可以抽象成以下一般的数学网络模型，本文称之为最小双费用流问题：

其中，{fij}为关于w1的最小费用流，即{fij}为下面线性规划模型的最优解：

由于最小双费用流问题涉及两个费用权w1和w2，因此也称之为最小(w1,w2)费用流问题。本文将重点研究求解最小双费用流问题的方法，并提出一种双层原始对偶算法。

在本文中所使用的概念和记号除特别声明外，均见文献[1]。另外，不失一般性，假设文中所涉及的网络均是简单的。

3 双层原始对偶算法

3.1 预备知识

由假设知，D是简单网络，即D中任意一对节点间只有一条弧，故A+(f)∩A-(f)=∅，记A(f)=A+(f)∪A-(f)。并且对∀(vi,vj)∈A(f)，令:

其中，k=1,2。

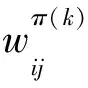
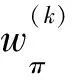
3.2 双层原始对偶算法的思想与步骤

步骤2 若v0=v(f)，结束，f为网络D中的最小(w1,w2)费用流；否则，转步骤3。

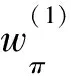
步骤6 沿由步骤5确定的P对f增广，其中增广的流值δ=min{c(P),v0-v(f)}，转步骤2。

3.3 算法正确性分析

下面的两个定理保证了双层原始对偶算法的正确性。

(2)G′(π(2))中任意一条(vs,vt)路都是D(f)中的最小(w1,w2)费用路。

证明

□

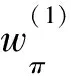
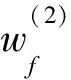
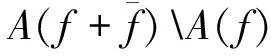
综上有定理得证。

□

定理3 如果双费用权网络D中存在双费用都可以达到最小的可行流，那么运用双层原始对偶算法求出的解必定也是两种费用都达到最小的。

□

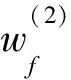
事实上，一旦在一个双费用权网络中确定了费用的主次，即可运用上述的双层原始对偶算法来求解出最小双费用流及其费用值。

3.4 算法复杂性分析

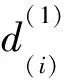
3.5 算法的进一步推广

上文分析的是在带容量限制的双费用权网络中求解最小双费用流的问题。类似地，如果将问题推广到带容量限制的k费用权网络中，要求解最小k费用流问题，那么只需将上述算法稍作改进。首先求出只由第一主费用的最小费用路构成的子网络G；然后在G基础上求出只由第二主费用的最小费用路构成的子网络G′，再在G′的基础上求出只由第三主费用的最小费用路构成的子网络G″…，依此类推，一直求到由第k主费用的最小费用路构成的子网络G*；最后将流值沿G*上的(vs,vt)路增广到v0即可。可以看到，本文的算法具有巨大的应用价值。

4 算例

求解图1所示网络D中流值为6的最小双费用流。其中每条弧旁三个参数由前往后分别是弧容量、主单位费用和次单位费用。

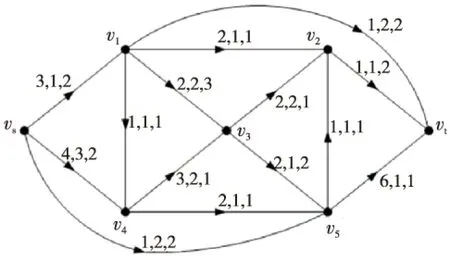
Figure 1 Netwok D图1 网络D

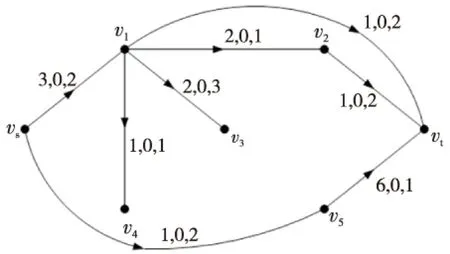
Figure 2 D′(f,π(1))图2 D′(f,π(1))

Figure 3 G′(π(2)) before augmentation图3 未增广时的G′(π(2))

接下来，类似地重复上述操作计算。由于G′(π(2))每条弧的参数中主单位费用和次单位费用均为0，为简便起见，在后面的作图中对图G′(π(2))的弧的参数只保留弧容量一项。

分别求出D′(f,π(1))和G′(π(2))，G′(π(2))如图4所示，可找到增广路P=vsv1vt，沿其增广流值1，此时，v(f)=2<6，返回步骤2继续执行算法；再次分别求出D′(f,π(1))和G′(π(2))，G′(π(2))如图5所示，可找到增广路P=vsv1v2vt，沿其增广流值1，此时，v(f)=3<6，返回步骤2继续执行算法。

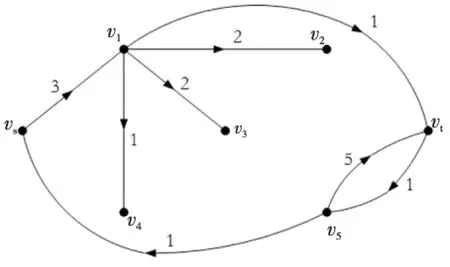
Figure 4 G′(π(2)) after the 1st augmentation图4 增广1次后的G′(π(2))

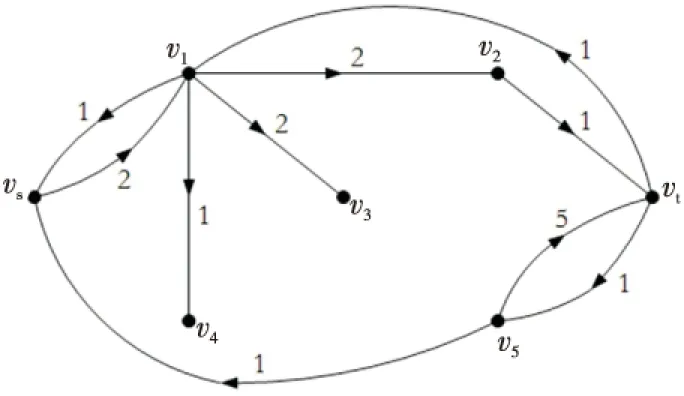
Figure 5 G′(π(2)) after the 2nd augmentation图5 增广2次后的G′(π(2))

分别求出D′(f,π(1))和G′(π(2))，G′(π(2))如图6所示，可找到增广路P=vsv1v4v5vt，沿其增广流值1，此时，v(f)=4<6，返回步骤2继续执行算法；继续分别求出D′(f,π(1))和G′(π(2))，G′(π(2))如图7所示，可找到增广路P=vsv4v5vt，沿其增广流值1，此时，v(f)=5<6，返回步骤2继续执行算法。

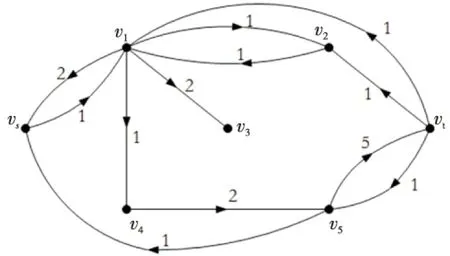
Figure 6 G′(π(2)) after the 3rd augmentation图6 增广3次后的G′(π(2))

Figure 7 G′(π(2)) after the 4th augmentation图7 增广4次后的G′(π(2))

再次分别求出D′(f,π(1))和G′(π(2))，G′(π(2))如图8所示，可找到增广路P=vsv4v3v5vt，沿其增广流值1，此时，v(f)=6，算法结束，所求得的可行流f为最小双费用流，如图9所示。

Figure 8 G′(π(2)) after the 5th augmentation图8 增广5次后的G′(π(2))

Figure 9 Flow scheme of f图9 流f的流方案

5 结束语

本文在了解多目标优化问题研究现状的前提下，通过对时下热点天基信息网络路由的讨论分析，抽象出含主次双费用的双费用权网络和相应最小双费用流问题的模型，给出了其线性规划形式，并给出了一种双层原始对偶算法，巧妙地解决了最小双费用流问题。之后证明了算法的正确性，分析结果说明算法拥有令人满意的复杂度。本文对算法的改进推广使其能求解一般多费用权网络的最小多费用流问题。最后的例子演示表明，算法的执行是行之有效的。

[1] Xie Zheng, Li Jiang-ping. Network algorithms and complexity theory[M]. 2nd edition. Changsha:National University of Defense Technology Press, 2003.(in Chinese)

[2] Klein M. A primal method for minimal cost flows with applications to the assignment and transportation problems[J]. Management Science, 1967, 14(3):205-220.

[3] Edmonds J, Karp R M. Theoretical improvements in algorithmic efficiency for network flow problems[J]. Journal of the ACM, 1972, 19(2):248-264.

[4] Ahuja R K, Magnanti T L, Orlin J B. Network flows:Theory, algorithms, and applications[M]. London:Prentice Hall, 1993.

[5] Wang Huan-xiong, Li Xi-jun. Optimal analysis of the path of the network with double weights[J]. Journal of Jilin Institute of Chemical Technology, 2001, 18(2):64-66.(in Chinese)

[6] Zhu De-tong. Dual theories of general multicommodity minimal cost flow problems[J]. OR Transactions, 2002, 6(3):17-26.

[7] Sun Xiao-jun, Jiao Jian-min. An algorithm for the problem of finding the minimal-cost path with the minimal time[J]. Computer Engineering & Science, 2008, 30(7):77-78.(in Chinese)

[8] Coello Coello C A. Evolutionary multiobjective optimization:A historical view of the field[J]. IEEE Computational Intelligence Magazine, 2006, 1(1):28-36.

[9] Ao You-yun, Chi Hong-qin. Differential evolution algorithm for multi-objective optimization[J]. Computer Engineering & Science, 2011, 33(9):88-94.(in Chinese)

[10] Wu Run-xiu. Double weighted hierarchical network algorithm based on granular computing[J]. Computer Engineering and Applications, 2011, 47(24):77-87.(in Chinese)

附中文参考文献：

[1] 谢政，李建平. 网络算法与复杂性理论[M].第二版. 长沙:国防科技大学出版社, 2003.

[5] 王焕雄, 李喜军. 双权网络路径的最优化分析[J]. 吉林化工学院学报, 2001, 18(2):64-66.

[7] 孙小军, 焦建民. 一种求解最少时间最小费用路问题的算法[J]. 计算机工程与科学, 2008, 30(7):77-78.

[9] 敖友云, 迟洪钦. 多目标优化差分进化算法[J]. 计算机工程与科学, 2011, 33(9):88-94.

[10] 吴润秀. 基于粒计算的双权网络分层算法[J]. 计算机工程与应用, 2011, 47(24):77-87.

MA Yu-bin,born in 1988,MS candidate,his research interest includes network optimization.

谢政(1960-),男,湖南衡阳人，教授，研究方向为组合最优化。E-mail:xiezheng@nudt.edu.cn

XIE Zheng,born in 1960,professor,his research interest includes combination optimization.

陈挚(1965-),男,湖南湘乡人，硕士，副教授，研究方向为组合最优化。E-mail:chenzhi@nudt.edu.cn

CHEN Zhi,born in 1965,MS,associate professor,his research interest includes combination optimization.

An algorithm to solving minimum double-cost flow problem

MA Yu-bin,XIE Zheng,CHEN Zhi
(College of Science,National University of Defense Technology,Changsha 410073,China)

Multi-objective optimization is a critical part of network optimization. The paper derives a minimum double-cost flow problem in double-cost network model with limitations on capacity from a practical case. According to the thought of hierarchy and the feature of double-cost network, the corresponding minimum double-cost flow problem is introduced and a two-layer primal-dual algorithm is proposed to solve it. The correctness of our algorithm is proved and its complexity is estimated asO(n2v0). Besides, the algorithm is improved to solve the minimumk-cost flow problem ink-cost network. Finally, a case is used to exhibit how the algorithm works.

double-cost network;minimum double-cost flow;two-layer primal-dual algorithm;complexity

2012-06-21;

2012-12-19

1007-130X(2014)03-0446-06

TP301.6

A

10.3969/j.issn.1007-130X.2014.03.012

马宇斌(1988-),男,广东台山人，硕士生，研究方向为网络最优化。E-mail:jhun31@126.com

通信地址：410073 湖南省长沙市国防科学技术大学理学院学员五队

Address:Team 5,College of Science,National University of Defense Technology,Changsha 410073,Hunan,P.R.China