模糊滑模控制在数控转台伺服系统中的应用

姜 静，吕恩辉

(沈阳理工大学 信息科学与工程学院，辽宁 沈阳 110159)

电气伺服系统的性能常常受到机械摩擦、外部扰动以及非建模动态特性等非线性和不确定性因素的影响，故其位置控制精度问题便受到人们的广泛关注。

滑模控制是一种非连续性控制，它可将被控对象的运动从任意位置控制到滑模曲面上并仍使系统保持稳定性和鲁棒性。然而，在实际滑模控制系统的应用中由于存在切换开关等非线性因素的影响，会使滑动模态产生高频抖振，抖振可能增加机械损耗，激发系统中的高频未建模动态等，这是防碍滑模变结构控制被广泛应用的主要因素。因此，设计一种能够削弱抖振的滑模控制器具有重要的理论和实际应用意义[1-2]。

本文针对具有外部摩擦干扰的数控转台伺服系统，提出了一种模糊滑模控制策略。通过将模糊控制理论和滑模变结构控制理论相结合，此控制器保持了常规滑模控制器的优点，具有良好的鲁棒性和精确的跟踪精度，并有效削弱了滑模变结构控制中出现的抖振现象[3]。

1 转台伺服系统模型

以某数控转台伺服系统为例，由于摩擦等非线性环节，使系统具有参数摄动和外在扰动等非线性因素[4]，系统结构如图1所示，系统模型图如图2所示。

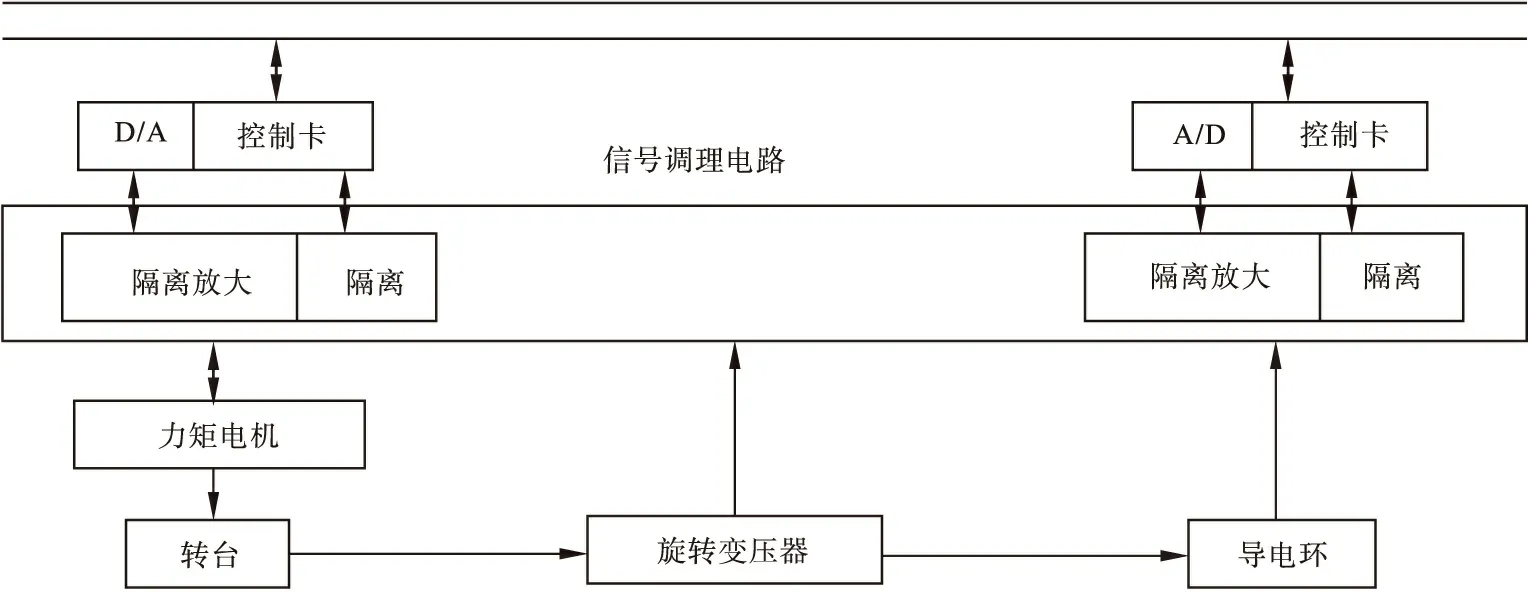
图1 转台伺服控制系统的结构

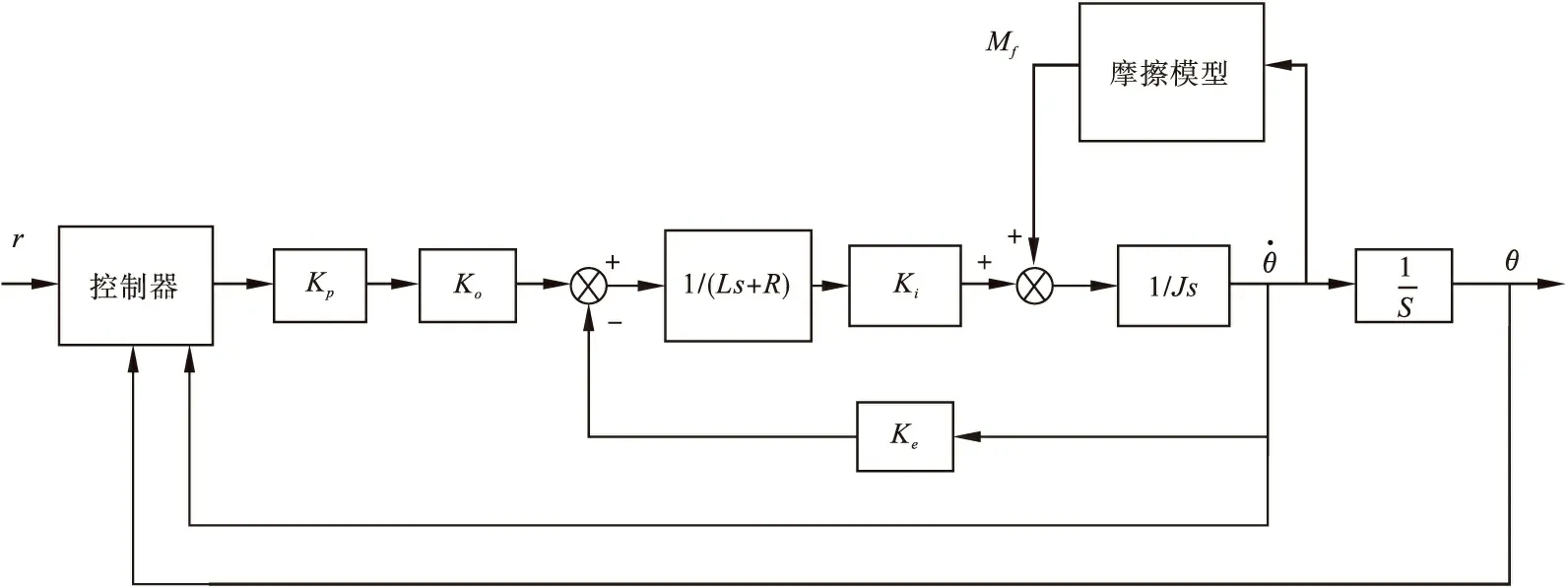
图2 转台伺服控制系统的模型

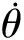
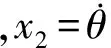
(1)

经变换可得到系统的状态方程为

(2)

2 滑模面设计

(3)

式中，x∈Rn，u∈R。

设被控对象为

x(n)=f(x,t)+g(x,t)u(t)

(4)

输入为r，即为系统期望的转角，设e为系统跟踪误差，即：

e(t)=r(t)-θ(t)

(5)

设计一个具有积分的滑模面为

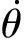
(6)

式中k1和k2为非零正常数。

在她看来，Adobo就是中文译为“阿道包”，最受菲律宾人欢迎的美食，也是菲律宾最传统的特色美食，用醋、酱油、黑胡椒、大蒜和月桂叶腌制的鸡肉或猪肉做成，据说也有腌制八爪鱼的，实质上与粤菜中的糖醋肉口味略似，但又更浓也更辣。

(7)

通过确定k1和k2，跟踪误差e(t)将趋近于零。

相比较于传统两输入模糊控制器来说，利用切换函数s(t)作为模糊控制器的输入，可以构成一个单输入的模糊系统，因而大大减少了模糊规则的数量[5]。

3 模糊控制器设计

3.1 定义输入输出模糊集

模糊子集可以作如下方式划分：{负大，负小，零，正小，正大}={NB，NS，ZO，PS，PB}。

已知s为模糊控制器的输入和Δu为控制器的输出,则模糊集为

s={NB,NS,ZO,PS,PB}

Δu={NB,NS,ZO,PS,PB}

其论域为

s={-3,-2,-1,0,+1,+2,+3}

Δu={-4,-3,-2,-1,0,+1,+2,+3,+4}

3.2 定义输入输出隶属函数

对于模糊控制器的输入s和输出Δu，这里采用3种形状的隶属函数分别为smf、trimf和zmf作为模糊变量的隶属函数曲线，如图3和图4所示。

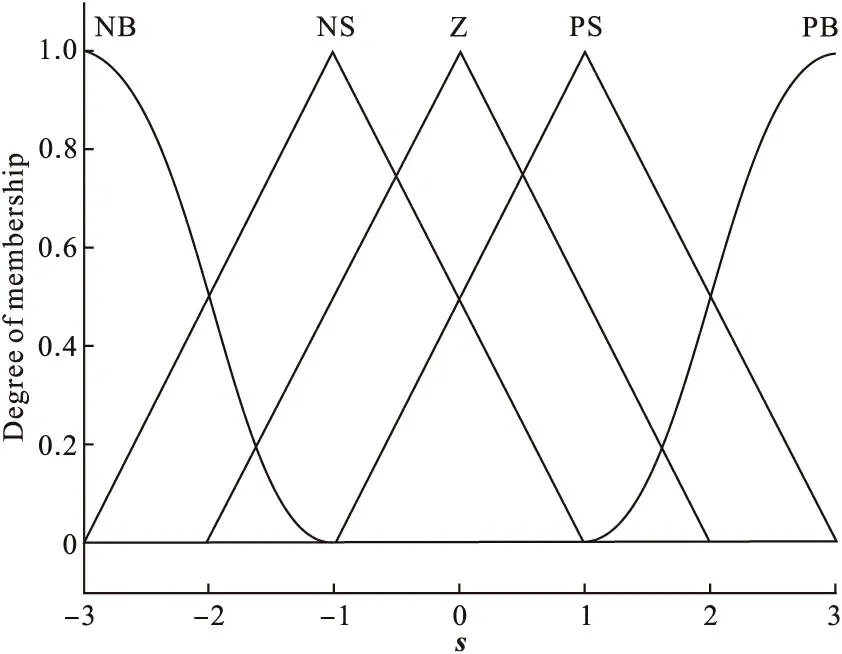
图3 模糊输入隶属函数

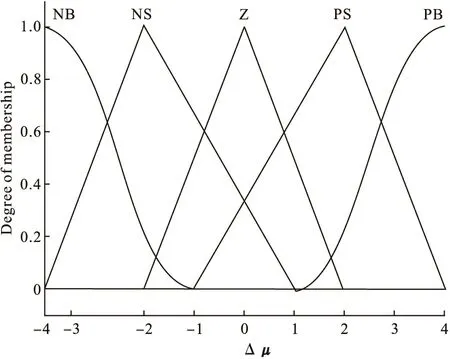
图4 模糊输出隶属函数

3.3 建立模糊控制规则

此控制器为单输入模糊系统，根据专家经验，采用Zadeh推理法在模糊系统中建立5条模糊规则：

(1)IF (sis NB ) THEN (Δuis PB )

(2)IF (sis NS ) THEN (Δuis PS )

(3)IF (sis ZO ) THEN (Δuis ZO )

(4)IF (sis PS ) THEN (Δuis PS )

(5)IF (sis PB ) THEN (Δuis PB )

3.4 反模糊化

采用重心法进行反模糊化，得到控制器的输出：

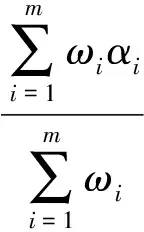
(8)

式中ωi为第i条规则的权值[7]。

4 仿真研究

根据上述方案，为了验证模糊滑模控制器的有效性，在Matlab7.1环境下，进行了系统的计算机仿真实验[8-9]，并与传统的滑模控制方法进行了比较。仿真程序控制的参数通过实验得到k1=8，k2=25。经仿真验证，k1和k2的选值直接影响到系统的性能。当k1值越大k2值越小，则系统响应过渡时间越长；当k1值越小k2值越大，则系统响应产生超调。系统仿真界面如图5所示。

图5 系统仿真界面

通过大量的仿真研究表明，模糊滑模控制不仅可以控制典型信号，而且对于随机生成信号也有较好的控制效果。仿真结果如图6～图9所示。

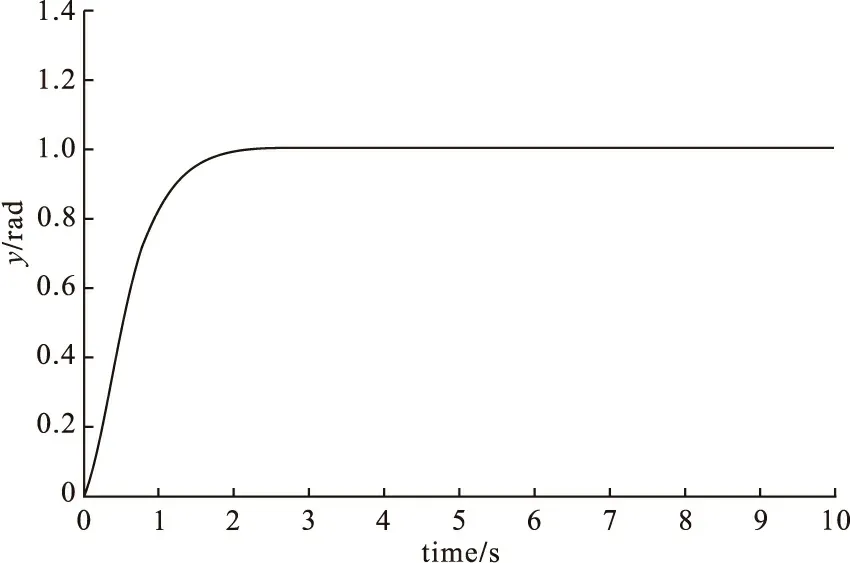
图6 传统滑模控制下的阶跃响应

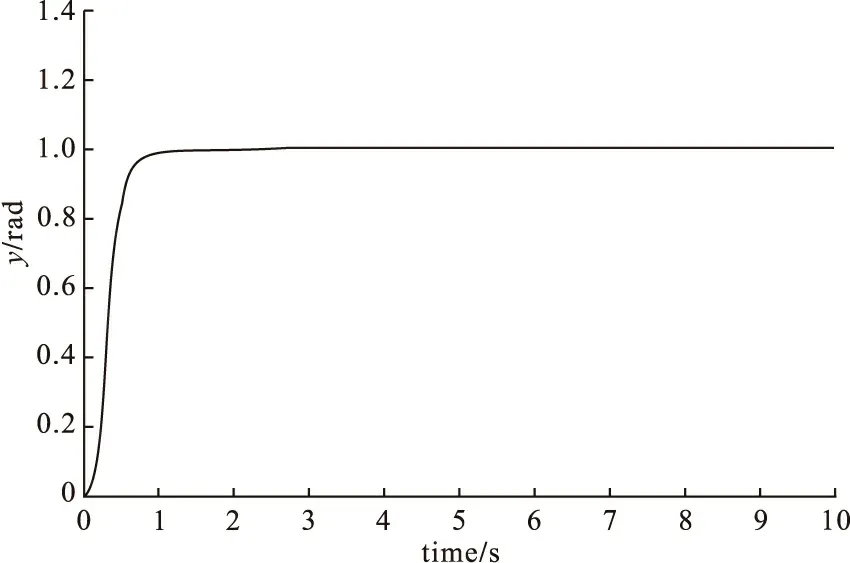
图7 模糊滑模控制下的阶跃响应

图6是无干扰下传统滑模控制的阶跃响应，系统过渡时间为1.68秒，响应曲线出现抖振现象；图7是无干扰下模糊滑模控制的阶跃响应，系统过渡时间为0.98秒，系统响应曲线较平滑，系统的稳态误差趋近于零。两图比较可知，模糊滑模控制具有更快的响应速度，能更有效地削弱系统的抖振。

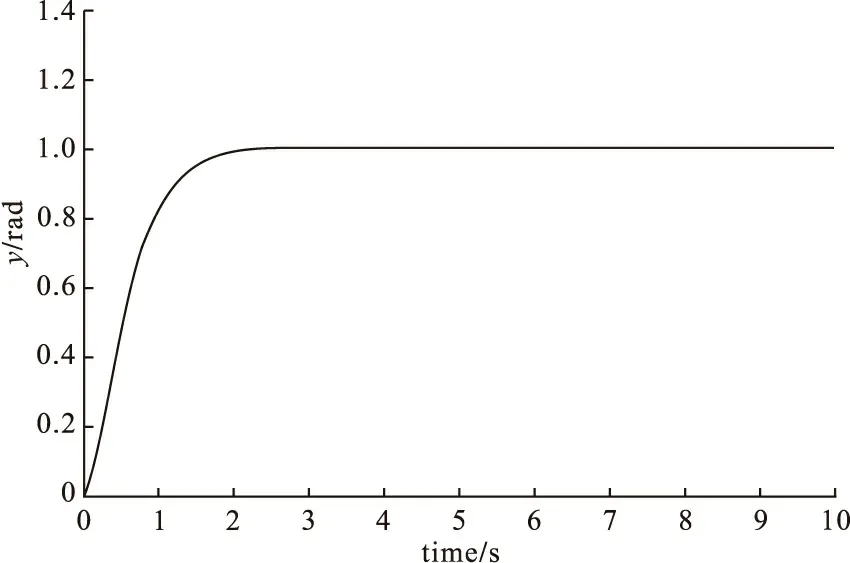
图8 传统滑模控制在常值干扰下的阶跃响应

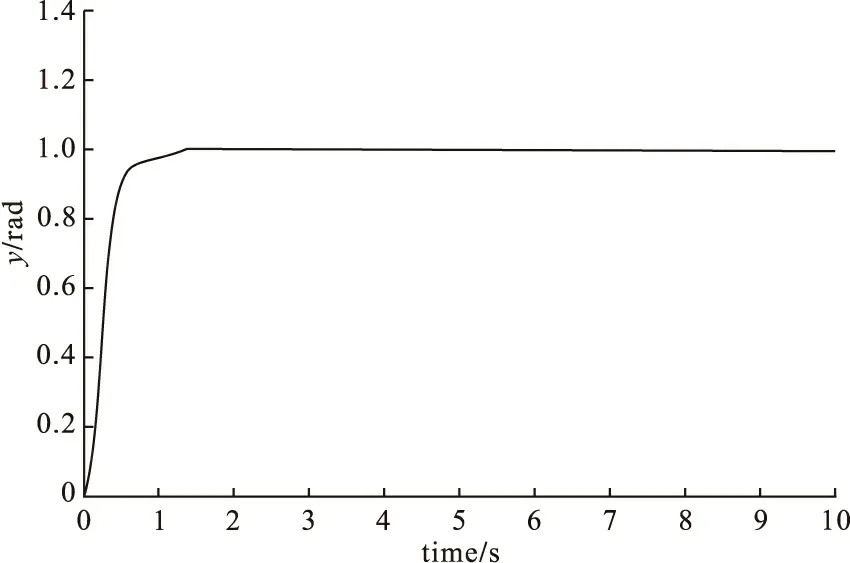
图9 模糊滑模控制在常值干扰下的的阶跃响应

图8是在常值干扰下传统滑模控制的阶跃响应，过渡时间为1.69秒，系统响应出现抖振现象；图9是在常值干扰下模糊滑模控制阶跃响应，系统过渡时间为1.0秒，响应曲线较为平滑。由仿真结果对比可以看出，模糊控制器不仅有更强的抗干扰能力，并且能得到较快的跟踪性能。

5 结论

针对具有不确定性和非线性因素的数控转台伺服系统，将模糊控制原理和滑模控制原理相结合，提出了一种模糊滑模控制算法。通过计算机仿真结果可看出，模糊滑模控制策略具有较快的响应速度和良好的鲁棒性。相较于传统滑模控制，模糊滑模控制能够柔化控制信号，并能减小或避免一般滑模控制中出现的抖振现象。

[1]闫凤光.数控转台环形力矩电机伺服系统模糊滑模控制的研究[D].沈阳：沈阳工业大学，2006.

[2]UTKIN A,GULDNER SHI J X.Sliding Mode Control in Electromechanical Systems[M].Taylor&Francis,1999.

[3]WAIR J,LIN C M,HSU C F.Adaptive fuzzy sliding-mode control for electrical servo drive[J].Fuzzy Sets and Systems，2004,143(2):295-310.

[4]谢磊.基于变结构控制策略的转台控制技术研究[D].南京：南京航空航天大学,2006.

[5]樊立萍,杨林.电气伺服系统的自适应模糊积分滑模控制[J].电力系统及其自动化学报,2010,22 (2):35-39.

[6]F.Barrero,A.Gonzalez,A.Torralba.Speed control of induction motors using a novel fuzzy sliding mode structure[J].IEEE Transactions on Fuzzy Systems,2002,10(3):375-383.

[7]傅春.模糊滑模控制系统的研究[D].上海：上海交通大学,2001.

[8]刘金琨.滑模变结构控制MATLAB仿真[M].北京：清华大学出版社，2006.

[9]Liu Jinkun,Er Lianjie.Sliding Mode Controller Design for Position and Speed Control of Flight Simulator Servo System with Large Friction[J].Systems Engineering and Electronics (China),2003,14(3):59-62.