采用TTT变换的混联系统预防维修策略分析
岳 磊,张民悦
(兰州理工大学理学院,甘肃 兰州 730050)
随着现代科技和工业的发展,机械系统大型化、复杂化、自动化和速度化越来越高,可以说信息时代对可靠性理论提出了新的挑战,同时也为可靠性理论的发展提供了前所未有的机遇和空间。混联系统是指系统由n个部件串联和并联混合而成,最常见的混联系统有串-并联系统和并-串联系统两种。可修混联系统的可靠性维修问题是系统可靠性研究的重要内容之一。目前该系统已被用于机械系统、电子元件系统以及质量与控制系统等工程领域。年龄更换策略是最常见的维修策略之一,在一些早期的研究工作中,人们广泛地研究年龄更换策略[1-4].曹晋华[1]假定元件的失效率为常量和变量时,分别给出了常见的混联系统的系统可靠度和平均寿命的计算方法;师小琳[5]在逐次截尾样本下,研究电子元件混联系统可靠性指标的估计问题。实验总时间(Total Time on Test),即TTT变换函数是在50年代,Epstein & sobel提出的实验总时间概念的一个推广。Barlow and Camp[6]利用TTT变换对失效数据进行统计分析,并且利用TTT变换研究了各个寿命分布类的特征。通过研究不难发现TTT变换在许多实际与理论应用中是一个有力的工具。如在寿命数据的统计分析中,它有助于人们选择合适的分布类型来拟合样本数据[7-9]。Nair and Sankaran[10]、Li Jinlin[11]、Bergman and Klefsjö[12]研究了TTT变换函数在其它方面的应用,例如经济学和风险评估等。在年龄更换策略的讨论中,用TTT变换可以确定最佳的更换年龄。Bengt Klefsjö[12-14]利用TTT探讨了可修设备更一般的年龄更换模型。Rao,K.R.M.and Prasad,P.V.N.[15-16]讨论了一些上面提到的TTT变换图形工具来分析材料处理设备操作在采矿业或推土机发动机的故障数据和计划维修时间间隔。Zydrunas Vagnorius[17]分析了TTT变换函数确定金属切削工具的最优更换时间,其磨损模型服从威布尔分布。他们已经对TTT变换函数的应用问题做了重点研究,提高了TTT变换的实际应用价值和应用广泛度。本文利用TTT变换函数解决混联系统目标规划的多目标问题,对上述情形作TTT变换,利用TTT变换图求解最优更换时间间隔T值,并且根据具体的数值分析其维修周期。
1 TTT变换的概念
设F是一个左连续的寿命分布。令
F-1(t)=inf{x≥0:F(x)≥t}
(1)
定义1
(2)

(3)
定义2
(4)
称作正则化的TTT变换函数(ST函数)。为简单起见,用φ来代替φF(t)。
TTT变换函数φ(t)对t递增,由于φ(t)已经正则化,故φ(t)的图形在一个单位的正方形中。对此,可以通过观察TTT变换图像,并计算出φ与t之间的关系。
定义3

2 混联系统模型与预防维修问题
2.1 混联系统模型
决定系统的输入与输出之间的功能模型或者数学模型完成这一过程,需要有关被研究的系统的知识,即工程背景知识。例如在液晶电视接收机中,其系统的部分核心包括公共通道,与此连接的有亮度通道、色度通道以及伴音通道等,组成混联系统部分框图,如图1所示。

图1 液晶电视机组成部分框图
可以建立上述公共通道与输出之间的系统核心部分为混联系统模型,该模型抽象为包括四个元件构成的系统,元件1与元件2并联后再与元件4串联,再由这个子串联系统与元件3构成并联系统(见图2)。
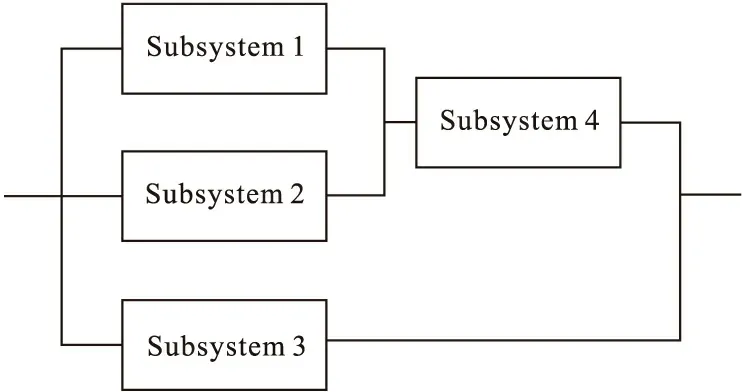
图2 混联系统图
元件所处的状况为系统的输入,系统所处的状况为系统的输出。设四个元件的可靠度分别为Ri=1-Fi(i=1,2,3,4),其中Fi为元件的分布函数,则系统的输入与输出的关系为
Ri=1-{1-[1-(1-R1)(1-R2)]·R4}(1-R3)
(5)
根据上述内容与图2所示的混联系统模型,可以假设各元件的寿命均服从参数为λ指数分布,分布函数为Fi(t)=1-exp(-λt),(i=1,2,3,4)。根据式(5)可以得到系统的可靠度为

=1-(1-2e-2λt+e-3λt)(1-e-λt)
=e-4λt-3e-3λt+2e-2λt+e-λt
(6)
2.2 混联系统预防维修问题
预防维修是一种计划性的维修活动,最常用的形式是定期检修。进行预防性的维护和检查,使得设备总体保持良好的工作状态,是企业和工厂日常运行过程必须进行的一项工作,一种典型的检查方法是定期保养或维修。从现代科学技术的发展来看,机械系统日益复杂化,不论是定期保养、定期维修、定期检查及定期更换等等,都是为了提高产品的寿命,提高产品的使用效率,最终目的是减少期望损失,以致使用费用最低且利润最大。故预防性维修,即故障前的维修显得尤为重要,这就是所说的年龄更换模型,如图3所示。
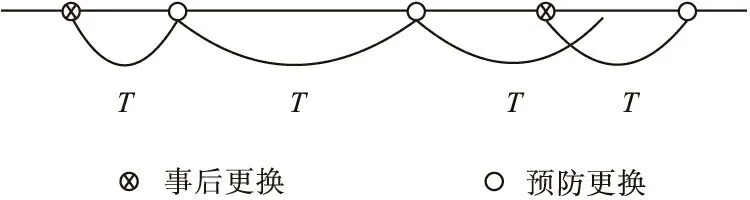
图3 年龄更换模型

(7)
和


(8)


图4 TTT变换图
观察TTT变换图不难发现,通过点(-a,0)和(-b,0)与TTT图相交的直线,只需此直线有最大斜率,交点的横坐标t*即为所求。
3 算例分析
假设某液晶电视机内部组成的部分混联系统的各元件寿命均服从参数为λ=2的指数分布,分布函数为Fi(t)=1-exp(-λt),(i=1,2,3,4),平均预防维修时间和事后维修时间分别为Tp=1,Tf=2;事后更换费用和预防更换费用分别为cf=9,cp=3,有a=0.5,b=1,我们根据定义,可以得到TTT变换函数为
(9)
F-1(t)=log(Z1)/λ
(10)

(11)


表1 TTT变换表
根据表1所示数据,利用Excel软件中函数功能,为了更好地精确拟合图中数据,故选用四次多项式,可以拟合出φ(t)=-2.4298t4+6.106t3-5.4388t2+2.7453t+0.0107 (如图5所示),继而根据TTT变换函数的定义内容,由Matlab软件,易得该混联系统的TTT变换图,故直接利用TTT变换图的方法来确定t*(如图6所示)。

图5 TTT变换函数的拟合
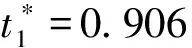
(12)
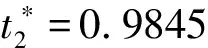
(13)

图6 TTT变换图
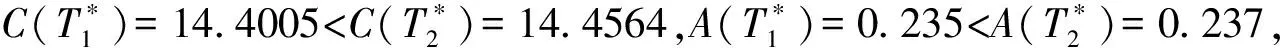
4 结束语
以复杂的混联系统中系统平均期望损失最小和平均可用度最大建立目标函数,利用TTT变换图的方法确定系统的预防维修周期,并分析年龄更换策略。该方法充分体现了TTT变换函数的计算结果中各指标对预防周期的影响,该方法对定周期的维修策略比较适用。但仍然可以从不同的预防维修策略的方向进行拓展研究,例如更加符合实际的满足几何过程的变周期维修策略,也可以运用TTT变换做研究,通过改进得到更满意的解,这样一来,TTT变换的应用范围更加广泛。
[1]曹晋华,程侃.可靠性数学引论[M].北京:科学出版社,2006:3-321.
[2]程侃.寿命分布类与可靠性数学引论[M].北京:科学出版社,1999:121-131.
[3]黄祥瑞.可靠性工程[M].北京:清华大学出版社,1990:42-45.
[4]何庆.预防维修周期的数学模型[J].农业机械学报.2005,36(2):153-154.
[5]师小琳.逐次截尾样本下电子元件混联系统可靠性指标的EB估计[J].现代电子技术,2008,31(12):1-3.
[6]Barlow,Richard E.,Campo,et al.Total time on test processes and applications to failure data analysis[A].Reliability and fault tree analysis[C].Berkeley:The University of California,1975:451-481.
[7]Taizhong Hu,Yashi Wang,Weiwei Zhuang.New properties of the total time on test transform order[J].Probability in the Engineering and Informational Sciences,2012,26(1):43-60.
[8]Jaroslaw,Bartoszewicz,Magdalena Benduch.Some properties of the generalized TTT transform[J].Journal of Statistical Planning and Inference,2009,139(7):2208-2217.
[9]Nair N.Unnikrishnan,Sankaran P.G.,Kumar B.Vinesh.Total time on test transforms and their implications in reliability analysis[J].Journal of Applied Pro bability,2008,45(4):1126-1139.
[10]N.Unnikrishnan Nair,P.G.Sankaran.Some new applications of the total time on test transforms[J].Statistical Methodology,2013,10(1):93-102.
[11]李金林.TTT变换在生产管理的优化问题中的应用探讨[J].数理统计与应用概率,1990,9(5):32-36.
[12]Bengt Klefsjö.Reliability interpretations of some concepts from economics[J].Naval Research Logistics,1984,31(2):301-308.
[13]Bengt Klefsjö.TTT-plottinga tool for both theoretical and practical problems[J].Journal of Statistical Planning and Inference,1992,29(1-2):99-110.
[14]Bengt Klefsjö,&Ulf Westberg.TTT plotting and maintenance policies[J].Quality Engineering,1996,9(2):229-235.
[15]Rao K R M,Prasad P V N.Graphical methods for reliability of repairable equipment and maintenance planning[A].Reliability and Maintainability Symposium[C].Philadelphia,PA:IEEE Conference Publications,2001:123-128.
[16]Prasad P V N,Rao K R M.A study on optimal age replacement of dozer engines[A].Reliability and Maintainability Symposium[C].Las Vegas,NV:IEEE Conference Publications,2008:31-36.
[17]Zydrunas Vagnorius,Marvin Rausand.Determining optimal replacement time for metal cutting tools[J].European Journal of Operational Research,2010,206(2):407-416.

