雷达信号处理系统仿真设计

张 奎，毕明雪

(沈阳理工大学 装备工程学院，辽宁 沈阳 110159)

严重电子干扰和强环境背景噪声条件下，如何从被污染的雷达回波信号中提取并处理目标信号具有重要意义。目前常用的雷达信号处理算法有DP(Dynamic Programming)法和PF(Particle Filter)法等[1-4]。相比PF法，DP法对雷达信号检测的信噪比要求更低，但数次搜索累加的DP法对雷达信号的信噪比提高有限，对强噪声的免疫效果不理想[5]，且累加过程降低了该算法的实时性。因此，本文提出一种基于Lyapunov指数的雷达信号处理算法，建立相应的Duffing仿真模型，通过预处理得出模型阈值，保证强噪声背景下更好的对微弱雷达信号进行提取和处理。

1 雷达信号处理仿真系统设计

建立雷达信号处理系统的Duffing模型[5]。

(1)

(2)

(3)

令Y(t)=Q(t)R(t)[6]，则

(4)

(5)

由式(1)～(5)可得

(6)

运用代换

(7)

(8)

由式(6)～(8)可得

(9)

雷达信号处理系统的Lyapunov特性指数l1和l2即为

(10)

利用Matlab Simulink软件搭建相应的雷达信号处理模型如图1所示。

2 雷达信号处理模型仿真

仿真参数设计：雷达信号频率为1GHz，正弦信号的角频率为2πGHz，强噪声为加性高斯白噪声。仿真软件为Matlab软件。

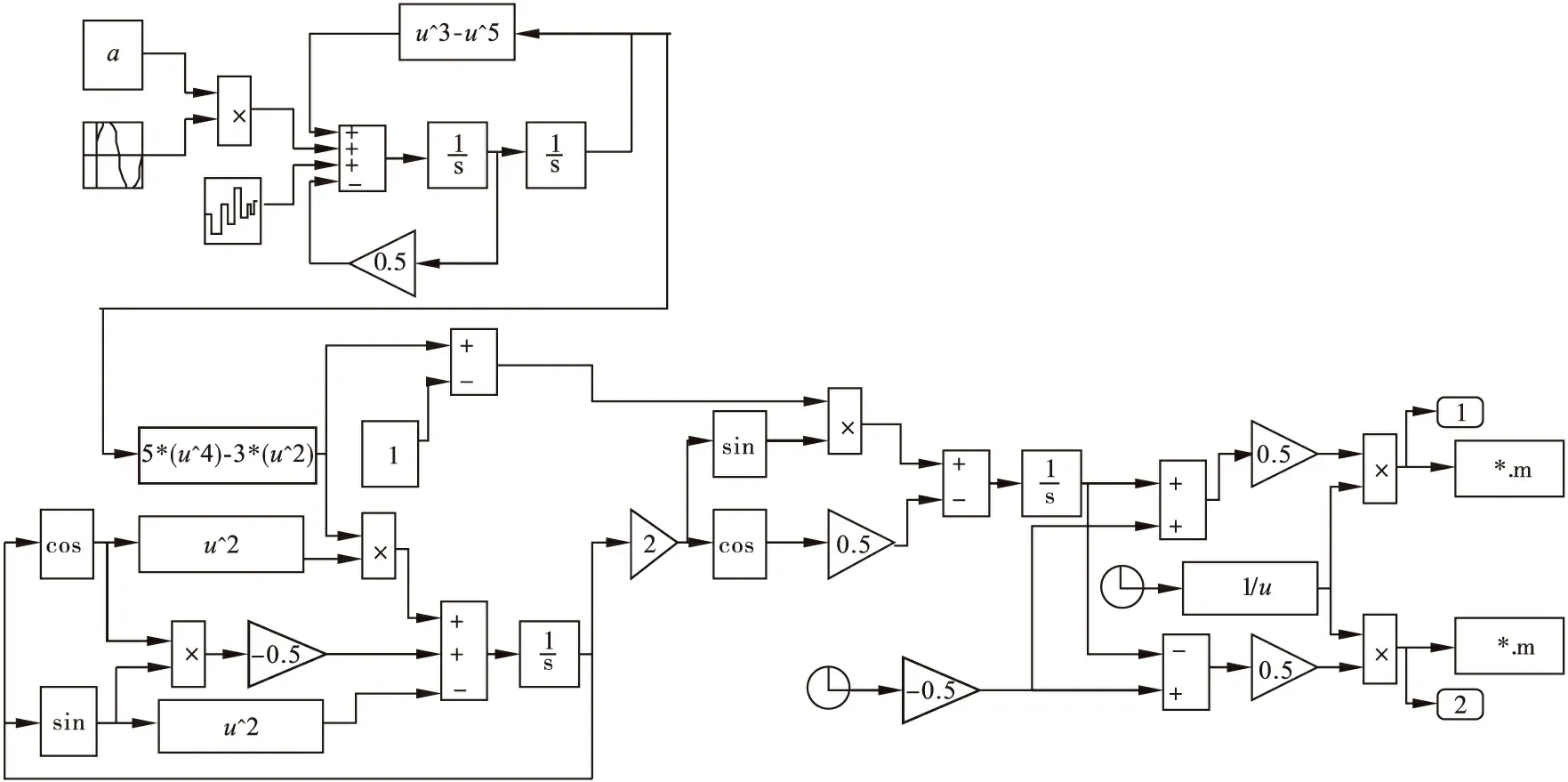
图1 雷达信号处理模型

2.1 阈值求解

首先需要对该模型由混沌态跃变为周期态的阈值进行求解。无噪声背景下，参数γ与Lyapunov指数的仿真曲线如图2所示。图2中，当最大Lyapunov指数大于零时，系统处于混沌状态，仅当上下两个Lyapunov指数均小于零(γ≥0.08237639)时，系统初次进入周期态，可确定系统由混沌态进入周期态的阈值γd=0.08237639。由于Duffing模型对γ值极为敏感，γ>0.16854134时，系统将处于周期态和混沌态的交替变化。由图2可以看出，该算法能够检测的雷达信号幅值范围应小于0.08616495。

图2 参数γ与Lyapunov指数的关系曲线

2.2 噪声背景下模型仿真

强噪声背景下，调节γ值等于γd，噪声功率范围为10-8W到1W，系统Lyapunov指数与噪声功率间的仿真结果如表1所示。由表1可以看出，当高斯白噪声功率P≤10-3W时，系统最大Lyapunov特性指数值均大于零，系统处于混沌状态。当噪声功率很大时，系统处于一种不稳定状态，但不会完全脱离混沌进入周期状态。因此，本文设计的雷达信号处理系统对一定功率范围内的白噪声是免疫的。

表1 Lyapunov指数与噪声功率的仿真结果

加入微弱谐波信号，模型如式(11)所示。

(11)

当幅值a由10-10递增至100时，经仿真得a≥7.6634×10-4时，最大Lyapunov指数为负，系统由混沌态跃变到周期态。此时，Lyapunov指数的演化曲线如图3所示。该系统的最低检测门限为10lg(7.6634×10-4)=-71.7388dB。

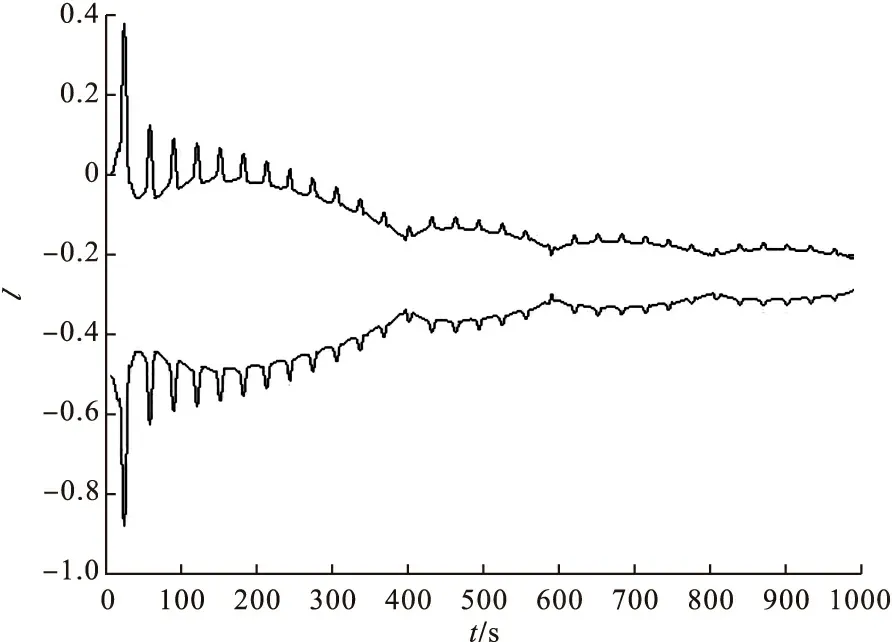
图3 Lyapunov指数的演化曲线

3 雷达回波信号处理仿真

3.1 回波信号频率检测

雷达回波信号处理系统的数学模型如式(12)所示。其中，γ2sin(ω2t)为回波信号中的有用信号，n(t)为回波信号中的噪声。对应的系统框图如图4所示。

(12)

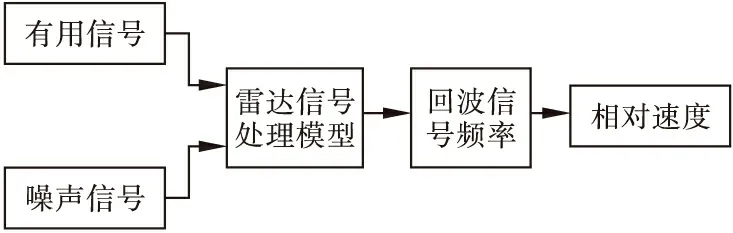
图4 雷达回波信号处理流程图

仿真过程中，首先调节系统模型参数为γd，使其处于临界混沌状态，加入的白噪声功率为10-4W，有用信号频率Fr=1.0000244GHz，ω1初始值为2πGHz。频率在一定范围内变化时，系统阈值基本不变，调节系统ω1值，仿真步长为10rad/s，当系统最大Lyapunov指数跃变为负值时，ω1=ω2=6283338490Hz。

3.2 相对速度求解

有用信号的频率为

Fr=ω1/2π

(13)

雷达信号的多普勒频移为

Fd=Fr-Ft=ω1/2π-Ft

(14)

Ft为发射信号的频率1GHz。则导弹与目标间的相对速度为

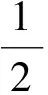
(15)

则导弹与目标间相对速度v=365.7m/s。

4 结论

本文提出了一种基于Lyapunov指数的雷达信号处理算法，并建立雷达信号处理的Duffing模型。根据该模型，求解出系统由混沌态跃变为周期态的阈值，进一步提取出回波信号中有用信号的频率，计算出导弹与目标间的相对速度。仿真结果表明，本文所提出的雷达信号处理模型的最低检测门限可达到-70dB以下，适用于强噪声背景下的雷达信号处理。

[1]Dellago C,Posch H A.Lyapunov Instability of the Boundary Driven Chernov Lebowitz Model for Stationary Shear Flow[J].Journal of Statistical Physics,2012,7(3):883-887.

[2]Samuel J D,Mark G R,Brian C A.Comparison of Dynamic Programming for Several Track before Detectal gorithms[J].Journal on Advances in Signal Processing,2010,5(11):1-10.

[3]强勇,焦李成,保铮.一种有效的用于雷达弱目标检测的算法[J].电子学报,2003,3(5):151-155.

[4]Blostein S D,Riehardson H S.A sequential detection approach to target tracking[J].IEEE International Conference on Communications,2011,1(1):59-62.

[5]李月,杨宝俊.混沌振子检测引论[M].北京:电子工业出版社,2004.

[6]张启明.离散Hamilton系统的Lyapunov型不等式及稳定性[D].长沙:中南大学,2012.