车载GPS/DR组合导航系统的数据融合方法研究

张丽平，李 环

(沈阳理工大学 信息科学与工程学院，辽宁 沈阳 110159)

车载GPS/DR组合导航系统的数据融合方法研究

张丽平，李 环

(沈阳理工大学 信息科学与工程学院，辽宁 沈阳 110159)

GPS/DR组合导航系统是非线性的，扩展卡尔曼滤波(EKF)可以利用线性化技巧将其转化为线性滤波问题，但这一过程会使得滤波结果出现很大误差。针对这一问题，将改进的粒子滤波方法(UPF)，即将无迹卡尔曼滤波(UKF)与粒子滤波(PF)相结合，应用到GPS/DR组合导航系统中，避免了EKF的线性化近似过程，同时优化了PF算法，提高了定位精度。实验结果表明，与 EKF和PF 算法相比，UPF算法具有更高的鲁棒性和更好的定位效果。

GPS/DR组合导航；扩展Kalman滤波；无迹Kalman滤波；粒子滤波

GPS/DR组合导航的关键技术是将全球定位系统(GPS)和航位推算(DR)两个系统输出的数据进行融合。在以往的组合导航中，一般是将GPS与DR系统作简单切换，系统正常工作时GPS作为主定位系统，当GPS信号较差或者丢失时便切换至DR系统[1]。一定程度上解决了GPS信号的失锁问题，但在复杂环境下，DR系统会随着时间的积累产生严重的误差。因此，将GPS与DR系统作简单切换已不能满足应用要求，需要采用合理的数据融合技术。国内外常用的数据融合技术有卡尔曼滤波、加权平均法、贝叶斯估计、统计决策理论、模糊推理和神经网络等。而在组合导航系统中，应用最广泛，最成功的数据融合技术是卡尔曼滤波[2]。

卡尔曼滤波应用在GPS/DR组合导航系统中的关键技术是将GPS和DR的信息同时用于定位解的求解过程中，使得DR系统的数据在滤波过程中不断得到修正，同时，DR系统的推算结果可用于补偿部分GPS定位中的随机误差，当GPS卫星信号被遮挡时由DR继续定位[3]。但是经典的卡尔曼滤波只适用于线性系统，而GPS/DR车辆组合导航系统的状态模型和观测模型都具有一定程度的非线性。有很多学者采用扩展卡尔曼滤波(EKF)[4]来进行GPS/DR组合导航的数据融合，但应用扩展卡尔曼滤波时所进行的线性化过程会导致滤波结果出现较大误差。

近几年,基于蒙特卡罗方法(Monte Carlo，MC)和递推贝叶斯估计的粒子滤波(Particle Filter，PF)算法备受广大学者关注。该方法不受非线性、非高斯问题的限制，可以处理强非线性和非高斯系统模型的数据融合。但粒子滤波也存在着一些问题，比如需要耗费大量的样本数去得到较精确的后验概率密度，重采样阶段也会造成样本有效性和多样性的损失，导致样本贫化现象等。

为了克服上述缺点，本文将改进的粒子滤波算法引入GPS/DR组合导航系统。以UKF为建议密度的粒子滤波方法，称为UPF算法(Unscented Particle Filter)[5]。UKF算法不需要像EKF算法一样进行线性化，因此避开了线性化过程造成的误差问题，并且UKF能够非常容易地将最新观测量引入状态估计。UPF算法首先使用UKF算法得到比PF算法更好的重要性分布函数，然后从中抽样得到粒子，最后再使用PF算法滤波。因此UPF算法能够大大提高粒子滤波的精度。

本文研究由经典卡尔曼滤波衍生的EKF算法，UKF算法和PF算法等融合算法，着重研究UPF算法以及UPF算法在GPS/DR组合导航系统中的应用。仿真结果表明UPF较EKF、PF具有更高的定位精度。

1 GPS/DR车载组合导航系统

1.1 状态方程的建立

车载GPS/DR组合导航定位系统的运动模型采用最为常用的“当前”统计模型[6]，通过卡尔曼滤波将观测到的信息进行融合，得到误差较小，精度较理想的位置和速度，从而达到较好的定位效果。

车载GPS/DR组合导航系统的状态向量为X=(e,ve,ae,n,vn,an)T，其中e和n分别为车辆东向、北向的位置分量，ve和vn分别为车辆东向、北向的速度分量，ae和an分别为车辆东向、北向的加速度分量。

系统的离散状态方程为

X(k)=Φ(k,k-1)X(k-1)+W(k-1)

(1)

式中:W(k-1)为系统噪声，状态转移矩阵为Φ(k,k-1)=diag{Φe,Φn}

(2)

式中：T为采样周期。

1.2 观测方程的建立

GPS/DR车辆组合导航系统的观测量分别来自GPS、角速率陀螺、里程计的信息。系统的观测量为Z=(egps,ngps,w,s)，其中egps和ngps分别为GPS接收机输出的东向、北向的位置坐标分量，ω为速度陀螺仪输出的角速度，s为里程计在采样周期内前进的距离。系统离散观测方程为

(3)

即：Z(k)=h[k,X(K)]+V(K)

(4)

式中:V(k)为观测噪声;v1(k)、v2(k)分别为GPS接收机东向、北向的输出误差;vω(k)、vs(k)分别为陀螺、里程计的输出误差。

2 粒子滤波(PF算法)

PF是一种基于蒙特卡罗方法和递推贝叶斯估计的滤波方法[7]，它采用一组从概率密度函数上随机抽取的并附带相关权值的粒子集来逼近后验概率密度，其中的核心算法是序贯重要性采样算法。序贯重要性采样算法(Sequential Importance Sampling，SIS)[8]是从重要性概率密度函数中生成采样粒子，并随着测量值的依次到来递推求得相应的权值，最终以粒子加权和的形式来描述后验概率密度，进而得到状态估计。粒子滤波在解决非线性、非高斯问题上具有很大的优越性，因此获得了广泛的应用，如应用在自动目标识别、移动机器人定位、计算机视觉、可视化跟踪等。

离散非线性状态空间模型：

xk+1=Φ(xk)+wk

(5)

yk=h(xk)+vk

(6)

式中：xk为系统维状态向量；Φ为n维向量函数；h为m维向量函数；wk为p维随机过程噪声；vk为q维随机观测噪声；yk为系统n维观测向量。

(7)

式中，δ(·)为狄拉克三角函数；令xi近似于q(x)，i=1,2,…,N,q(x)为重要性密度函数，N为粒子数。这样通过加权就可以得到密度p(xk)为

(8)

式中

(9)

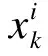
q(x0：k|y1:k)=q(xk|x0:k-1,y1:k)·q(x0:k-1|y1：k-1)

(10)

那么权重公式为

(11)

由于最常见的重要性密度函数选择为

(12)

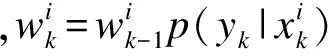
(13)

将该权值进行归一化得到归一化权值为

(14)

虽然PF算法是解决非线性非高斯问题的有效工具，但仍然存在问题。其中最主要的问题就是为了得到应用系统较为精确的后验概率密度需要耗费庞大的样本数据。因此本文通过改进的粒子滤波选择更好的重要性密度函数来提高滤波精度。

3 UPF算法

与EKF不同,UKF以UT变换为基础，摒弃了对非线性函数进行线性化的传统做法，采用卡尔曼线性滤波框架，对于一步预测方程，使用UT变换来处理均值和协方差的非线性传递，这样就形成了UKF算法[9]。其中UT变换的基本原理是在估计点附近确定性采样，这些采样点能完全得知状态随机变量的均值和协方差矩阵变换，然后通过泰勒展开的二阶精度逼近后验均值和协方差。因此UKF在减少采样粒子数的同时保证了逼近精度，有效克服了EKF算法估计精度低、稳定性差的缺陷。

UPF的具体步骤为

(15)

式中:Pw为系统噪声方差，Pv为测量噪声方差。

2)使用UPF算法更新粒子集

(16)

计算Sigma点：

(17)

式中：λ为合成比例参数

λ=α2(nα+κ)-nα,κ为缩放比例参数，它控制Sigma点到均值的距离，通常κ=0；0≤α≤1为缩放比例参数，它控制Sigma点的分布范围，通常取一个较小的数值，以避免在强非线性情况下产生采样的非局部影响；β≥0反应密度函数高阶矩信息，当高斯先验时β=2。

时间更新：

(18)

量测更新：

(19)

输出：

(20)

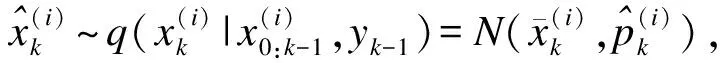
3)分别通过式(13)，式(14)对粒子进行权重计算和归一化。

4 仿真分析

X(0)=[0,10,0,0,10,0]，

P(0)=diag{202,12,0.22,202,12,0.22}

仿真时间为100s，采样粒子N=500；

系统噪声：Q=diag{10,1,0.1,10,1,0.1}；

量测噪声：R=diag{10,10,0.01,4}。

仿真结果如图1～图4和表1所示。

图1 东向位置误差

图2 北向位置误差

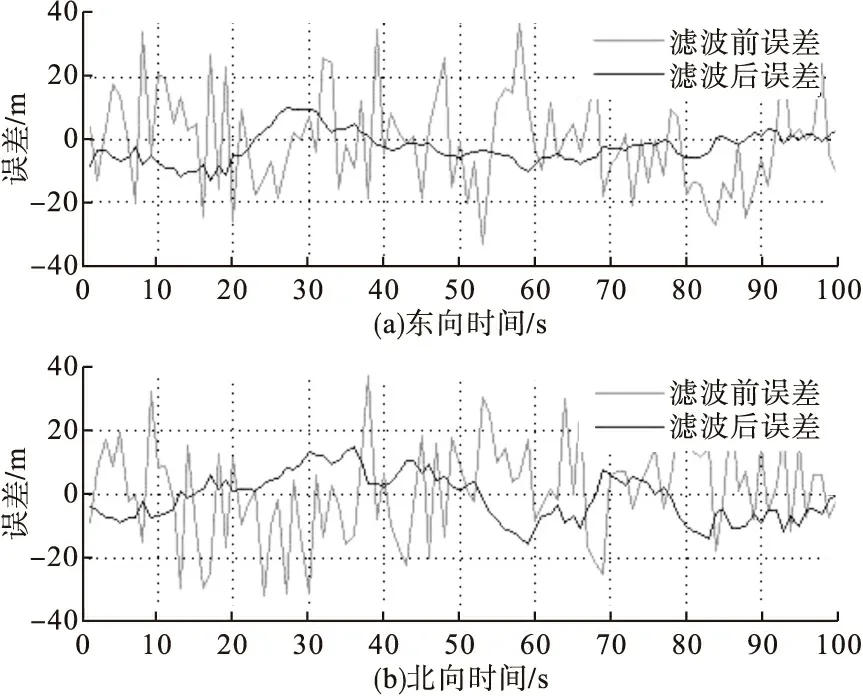
图3 UPF算法滤波前后比较

图4 UPF算法目标跟踪轨迹

表1 EKF、PF和UPF滤波误差比较

以上仿真图中，图1、图2和表1是EKF算法、PF算法、UPF算法在相同条件下的滤波结果。结果表明，EKF算法的滤波误差平均为10m左右，PF算法的滤波误差平均为5m左右，而UPF算法的滤波误差平均为3m左右，从而体现了UPF算法比其他两种算法有更好的定位精度。通过仿真图也可以明显看到，UPF算法的稳定性更好。图3为UPF算法滤波前后的误差比较，从图可以看出，通过UPF算法滤波后，误差明显减小，在水平线附近浮动范围很小，而滤波前误差则浮动很大。图4为UPF算法的目标跟踪轨迹，从图明显看到，UPF具有很高的定位精度。综上所述，不论是算法的稳定性，还是定位精度，UPF算法都优于其他两种算法。

5 结束语

研究了UPF算法在GPS/DR组合导航系统中的应用，并将其与EKF、PF算法进行比较。比较结果表明，UPF算法有效避免了EKF的线性化近似过程和PF算法严重的退化现象，具有较高的稳定性和更好的定位效果。因此，UPF算法在GPS/DR组合导航系统中具有更好的应用前景。

[1]吴富梅,杨元喜,田育民.GPS/DR 组合导航自适应 Kalman 滤波算法[J].测绘科学技术学报,2008,25(3):206-208.

[2]杨东凯,寇艳红,吴今培,等.智能交通系统中的地图匹配定位方法[J].交通运输系统工程与信息,2003,3(3):38-43.

[3]周翟和,刘建业,赖际舟,等.一种新的改进高斯粒子滤波算法及其在 SINS/GPS 深组合导航系统中的应用[J].控制与决策,2011,26(1):85-88.

[4]Kalman R E.A new approach to linear filtering and prediction problems[J].Journal of basic Engineering,1960,82(1):35-45.

[5]Van Der Merwe R,Doucet A,De Freitas N,et al.The unscented particle filter[C].NIPS.2000:584-590.

[6]周宏仁.机动目标“当前”统计模型与自适应跟踪算法[J].航空学报,1983,4(1):73-86.

[7]辛云宏,王保平,杨万海.基于序贯重要采样算法的被动单站机动目标跟踪[J].西安电子科技大学学报,2005,32(5):820-824.

[8]Arulampalam S.Maskell.A tutorial on particle filters for on line non linear/non Gaussian Bayesian tracking[J].IEEE Transactions on Signal Processing,2002,50(20):174-188.

[9]Julier S,Uhlmann J,Durrant-Whyte H F.A new method for the nonlinear transformation of means and covariances in filters and estimators[J].Automatic Control,IEEE Transactions on,2000,45(3):477-482.

[10]Arulampalam S.Maskell.A tutorial on particle filters for on line non-linear/non-gaussian bayesian tracking[J].IEEE Transactions on Signal Processing,2002,50(20):174-188.

ResearchonDataFusionMethodofVehicleGPS/DRIntegratedNavigationSystem

ZHANG Liping，LI Huan

(Shenyang Ligong University,Shenyang 110159,China)

GPS/DR integrated navigation system is a nonlinear system,which leads to a big error in realizing system linearization by using the extended Kalman filter (EKF).Aiming at solving the problem,the improved particle filter algorithm (UPF) combining the unscented Kalman filter (UKF) and particle filter (PF) is applied to the GPS/DR integrated navigation system.It not only avoids the linear approximation of EKF,but also optimizes the PF algorithm and improves the positioning accuracy.Experimental results show that,compared with the EKF algorithm and PF algorithm,UPF algorithm has higher robustness and better positioning effect.

GPS/DR integrated navigation;extended Kalman filter;unscented Kalman filter;particle filte

2013-06-25

张丽平(1987—)，女，硕士研究生；通讯作者：李环(1964—)，女，教授，研究方向:扩频通信技术及应用，信号处理等.

1003-1251(2014)01-00013-05

TN967.2

A

马金发)