一类带有交叉扩散项的捕食-食饵模型的共存态

赵 宝 娟

(天津大学 理学院，天津 300072)

1 引 言

近年来，由于捕食模型的广泛应用，国内外学者对其进行了广泛的研究.通过不断的改进模型，使其更加符合实际意义.在某些生态系统中，种群间的相互影响起着重要的作用.因此本文考虑了如下的捕食-食饵模型：

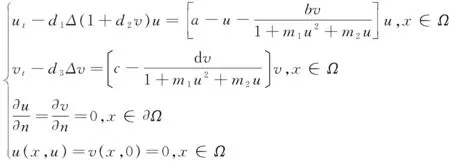
(1)

Ω是RN中的有界区域，且具有光滑的边界∂Ω，u(x,t)≥0,v(x,t)≥0分别表示捕食者和食饵的种群密度，其中t≥0，d为转化系数a，b，c，m1，m2均为正常数，d1，d2，d3为扩散系数，均为正常数，d3为非负常数.a，b，c都有一定的生物意义.

式(1)对应的平衡态问题是：

(2)

2 正解的先验估计

为了得到正解的先验估计，我们首先令U=(1+d2v)u，则式(2)可以等价的写成

(3)

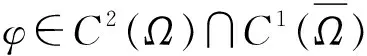
定理1 存在正常数G,H,使得式(3)的任何正解(U,v)一定满足：U(x)≤G,v(x)≤H.

证明对式(3)第一个等式左边乘U,第二个等式左乘v，然后在Ω上积分得：

(4)

(5)

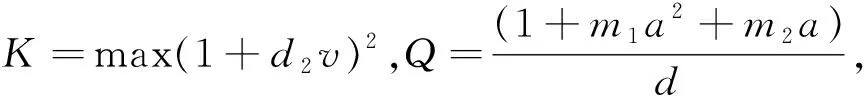
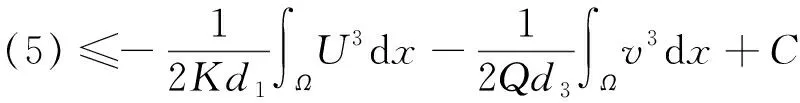
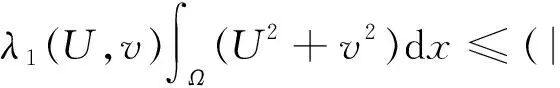
立即得到(U,v)均是有上界的.

定理2[2]令D为一个正常数，当d1,d3≥D时，存在正常数C*，使得式(3)的任何正解(U,v)满足U(x),v(x)≥C*.

证明：假设U(x),v(x)没有下界，则存在(d1,i,d2,i,d3,i)=(d1,d2,d3)，其中:d1,i,d3,i≥D,d2,i≥0使得式(3)对应的正解列(Ui,vi)满足minUi→0或者minvi→0,i→∞.由于(Ui,vi)满足式(3)，将其带入，并在Ω上积分得，

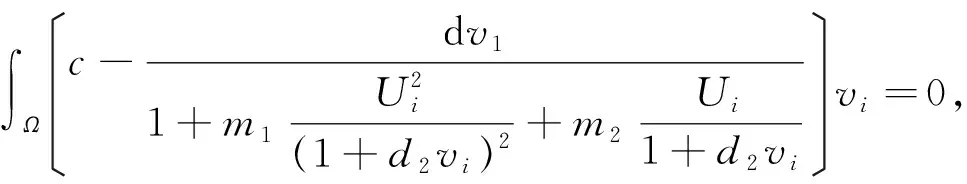
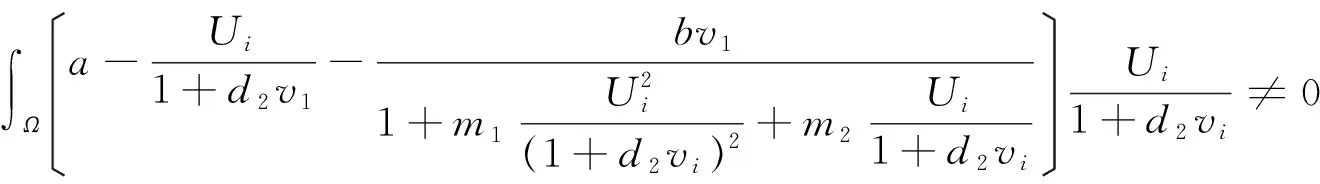
综合以上三种情况完成了定理证明[3].

3 非常数正解的不存在性

设0=λ0<λ1≤λ2≤…≤λn≤…→∞是-Δ算子在Neumann边界条件下的特征值，令

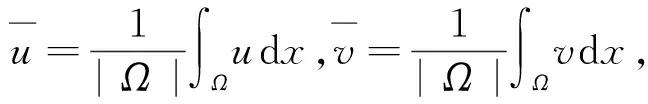
定理3 设D为一个正常数，ε为任意整数，如果d2>D，使得当

时，式(3)没有非常数正解.

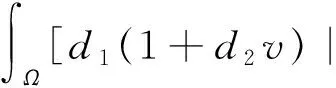
其中:ζ∈(0,a),C0,C1,C为正常数，ε,γ为任意的正常数，

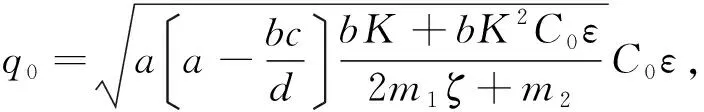
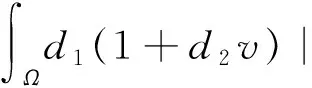
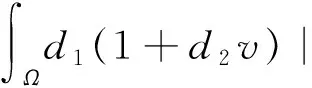
4 非常数正解的存在性

我们利用上面得到的先验估计和Leray-Schauder度理论来讨论非常数正解的存在性.

定义算子F=[F1(W)F2(W)]T，其中W=[Uv]T

(6)

由Leray-Schauder度理论可知，若0不是式(6)的特征值,则

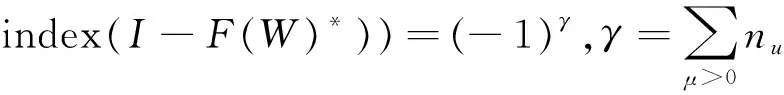
(7)

其中nμ是大于0的特征值μ的代数重数.

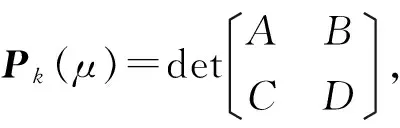
A=μ+

B=

C=

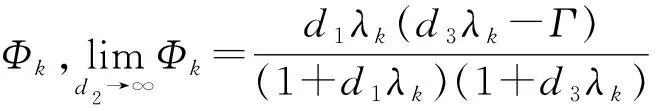
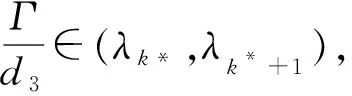
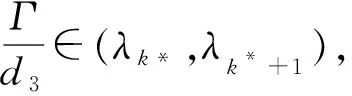
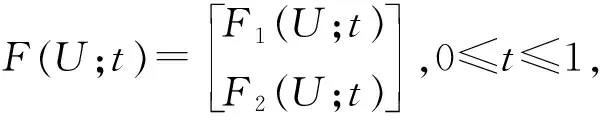
则式(3)的正解等价于F(U;1)的正解.由定理1和推论1可知，存在正常数M，使得

F(U;t)=0在上∂Θ对所有的t∈[0,1]没有正解，其中

deg(I-F(·，0),Θ,0)=deg(I-F(·，1),Θ,0)

由上述引理可知deg(I-F(·，t),Θ,0)=index(F(·，0),U*)=1

deg(I-G(·;1),Θ,0)=-1，矛盾.则(3)至少有一个非常数正解.

参考文献：

[1] PENG R, WANG M X, YANG G Y. Stationary patterns of the holling-tanner prey-predator model with diffusion and cross-diffusion[J].Applied Mathematics and Computation, 2011, 24(3): 570-577.

[2] 叶其孝, 李正元. 反应扩散方程引论[M]. 北京: 科学出版社, 1990.

[3] 王利娟, 姜洪领. 带交叉扩散的捕食模型非常数正解的存在性[J]. 中山大学学报, 2012, 51(1): 15-18.

[4] SMOLLER J. Shock waves and reaction-diffusion equation[M].New York: Spring-Verlag,1983.

[5] WONLYUL K, KIMUN R. A qualitative study on general gause-type predator-prey models with constant diffusion rats[J].Journal of Mathematical Analysis and Application, 2001, 131(2):321-324.

[6] 王 涛，刘冬华.融合混沌和捕食搜索的混合粒子群算法[J].哈尔滨商业大学学报：自然科学版，2013，29(3)：355-358