基于均值-方差准则下的套期保值问题研究

刘 峰，刘宣会

(西安工程大学 理学院，西安 710048)

投资组合选择模型研究的方法主要有2种: 一种是均值-方差分析，最终期望的收益最大而风险最小, 另一种是研究最优投资组合消费问题.进行投资组合研究的主要目的是分散非系统风险，而套期保值问题的研究是在投资组合研究的基础上使对冲其系统风险成为可能.未定权益的套期保值问题，是解决或有权益的出售者选择什么样的策略才能避免或尽可能降低因出售或有权益而在未来可能遭受的损失.

目前，最常用的选择最优套期保值策略的准则有2种，一种是由Bouleau和Lamberton提出的风险最小准则，另一种是由Folmer和Sondermann首次提出的均值一方差最优准则. 他们首先引入成本过程差的平方的条件期望作为风险度量，解决了折现价格为局部鞅的市场模型中的套期保值问题；Lars Schiefner[1]在不考虑交易费用的情况下，把期末未定权益折现成现金流的形式，运用风险最小化方法得到最优套期保值策略；刘海龙等[2]在标的资产价格服从带有随机方差几何布朗运动的非完全市场的假设条件下, 应用随机微分对策方法, 研究与标的资产有关的欧式期权的动态保值策略问题, 并证明该方法下得出的最优动态保值策略与用Black-Scholes套期比表示的delta 套期保值策略是一致的.Lin[3]进一步运用LQ方法研究了随机参数的连续时间均值-方差问题, 但其仅限于运用LQ方法求解了投资组合的有效边界, 并没有考虑投资组合的套期保值问题.刘宣会等[4]将随机LQ控制模型推广到系统状态为跳跃扩散过程的随机LQ控制问题, 然后运用该框架对金融中未定权益的套期保值问题和均值-方差模型进行了研究.王波等[5]研究了在一个时间连续的有交易的市场模型下, 美式未定权益的上、下套期保值的表达式, 并证明了上、下套期保值区间使所有无套利价格的集合.袁军和杨成[6]在连续时间情形、不考虑交易费用、市场无摩擦假设, 以及套期保值准则等条件下, 考察了参数随机的证券投资组合中加入未定权益类衍生品形成的最优动态投资策略, 并给出了该投资组合的最优模型所对应的黎卡提(Riccati)方程的解的存在性证明.

本文在文献[7]的基础上研究了现实中当出现重大信息时标的资产价格服从一跳跃扩散过程时，运用均值-方差准则及倒向随机微分方程研究套期保值问题，并得到最优套期保值策略.

1 模 型

设金融市场中有2种证券，一种为风险证券(设为股票)，另一种为无风险证券(设为债券)；股票价格为P(t)，P(t)服从下列随机微分方程：

(1)

债券价格为P0(t)，P0(t)服从下列方程：

(2)

其中：r(t)>0为无风险利率，μ(t)为股票收益率，σ(t)为波动率，W(t)为(Ω,F,P)上的标准Brown运动，N(t)为(Ω,F,P)上具有强度λ(t)的Poisson过程，且W(t)与N(t)独立.

为了讨论问题方便只考虑金融市场只有一个股票和一个债券，对于多个股票的处理与上述情况无本质性差异.

假设存在(A1)：

其中σ(t)可逆.

设投资者初始财富为X(0)=X0，π(t)表示t时刻投资者在股票上投资财富的市场价值，此时的财富过程为X(t)，那么

dX(t)=[r(t)X(t)+b(t)π(t)]dt+σ(t)π(t)dW(t)+π(t)φ(t)dN(t),

(3)

其中：b(t)=μ(t)-r(t).

设ζ为未定权益，我们寻找套期保值策略π(t)，使得J(X0:π(t))最小

(4)

2 模型求解

考虑下列BSDEs：

(5)

(6)

其中

命题2.1 假定存在(A1)，若BSDEs有惟一解(P(·),Λ(·)),(h(·),η(·))那么

(7)

是可容许策略.

设dN(t)=dM(t)+λ(t)dt，M(t)是鞅.

由伊藤公式，有

π(t)′φ(t)′π(t)]dM(t)

是鞅.对上述取期望得

另一方面，

合并前面方程，得

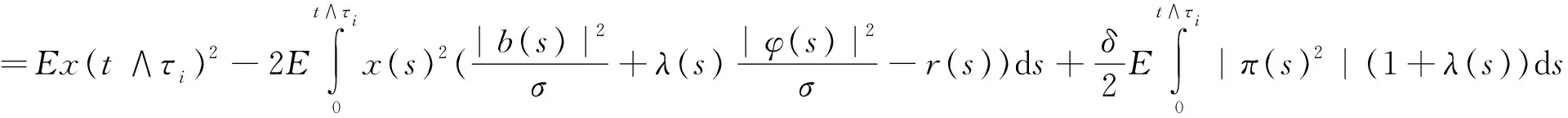
最后，由于σ(t)σ(t)′≥δI,λ(t)>0，得

把式(7)带入财富公式(3)得

(8)

命题2.2 在命题2.1假设的条件下，SDE有惟一解x(·)，且

证明：我们构造方程

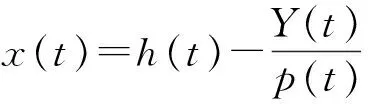
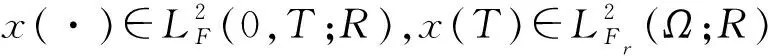
由伊藤公式得，

p(t)(h(t)-x(t))2=p(0)(h(0)-x(0))2+

≤p(0)(h(0)-x(0))2+

因为p(t)>δ,τi↑T,i→∞，由Fatou引理得

δE(h(t)-x(t))2≤Ep(t)(h(t)-x(t))2≤p(0)(h(0)-x(0))2+

因此，

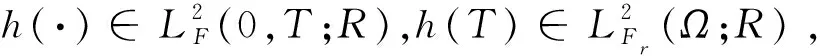
下面证明命题2.1

命题2.3 假设(A1)存在，若DSDEs(5)、(6)有惟一解，(p(·)，Λ1(·)，Λ2(·))，(h(·),η1(·),η2(·)),则式(7)是惟一最优控制策略，且

J*=p(0)(h(0)-x(0))2+

(9)

是随机控制问题式(4)的最优均值-方差套期保值策略.其中：

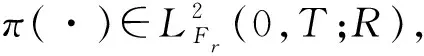
由伊藤公式得

dp(t)(h(t)-x(t))2=p(t)d(h(t)-x(t))2+(h(t)-x(t))2dp(t)+dp(t)d(h(t)-x(t))2

(10)

对上式在[0,T]积分并取期望，得

E(ζ-x(T))2=p(0)(h(0)-x(0))2+

上述结果与命题2.1一样，由假设p(t)>0,σ(t)是非退化的.

3 结 语

本文考虑现实中有重大信息出现时，股票价格服从跳跃-扩散过程时，研究了套期保值问题，应用倒向随机微分方程得到均值-方差准则下套期保值问题的最优套期保值策略.本文考虑了股票价格服从一般的跳跃-扩散过程.对股票价格服从带有马尔科夫调制参数的跳跃-扩散过程的情况，也可以建立模型，并推导出该模型下的最优套期保值策略，结果类似，但推导过程更加繁琐.

参考文献：

[1] LAMBERTON D, PHAM H, SCHWEIZER M. Local risk-minimization under transaction costs[J].Mathematics of Operations Research, 1998, 23(3): 585-612.

[2] 刘海龙, 吴冲锋. 基于鲁棒控制的期权套期保值策略[J].控制与决策, 2001, 16(6): 974-976.

[3] LIM A E B, ZHOU X Y. Mean-variance portfolio selection with random parameters inacomplete emarket[J].Mathematics of Operations Research, 2002, 27(1): 101-120.

[4] 刘宣会, 胡思建, 侯建荣. 证券组合优化模型的随机LQ控制框架[J].西安电子科技大学学报: 自然科学版, 2004, 31(2): 304-309.

[5] 王 波, 孟庆欣. 有交易费的美式未定权益的套期保值[J].复旦学报: 自然科学版, 2005, 44(3): 403-410.

[6] 袁 军, 杨 成. LQ理论在参数随机的证券投资组合套期保值中的应用[J].数学的实践与认识, 2008, 38(16): 33-37.

[7] LIM A E B. Quadratic hedging and mean-variance portfolio selection with random parameters in an incomplete market[J].Mathematics of Operations Research, 2004, 29(1): 132-161.