高超声速飞行器上升段轨迹设计

王 纯

(西北工业大学 航天学院， 西安 710072)

高超声速飞行器是以吸气式或组合式发动机为动力且能在大气层及跨大气层飞行的新型飞行器.由于高超声速飞行器具有射程远、机动性好、精度高等优点，很多国家制定了研制高超声速飞行器的计划，并进行了很多试飞实验[1].

每种空天飞行器都要经过上升段这个过程，高超声速飞行器也不例外.飞行器的上升段是保证飞行器能顺利达到预定轨道，确保完成飞行任务的基础，因此设计高超声速飞行器的轨迹也应从上升段着手.本文通过建立高超声速飞行器相关的模型，采用序列二次规划法设计并仿真了飞行器上升段的轨迹，结果表明这种优化方法能够适应飞行器受到的各种飞行约束，验证了轨迹设计的合理性和可行性，并为高超声速飞行器轨迹设计问题提供了一种有价值的研究方案.

1 上升段动力学方程

高超声速飞行器发射方式有很多种，本文主要研究类似火箭发射的陆基垂直发射方式.这种发射方式的特点是在上升段初期飞行器可以迅速爬升，通过对攻角的控制，使飞行器最终能以较小的轨迹倾角进入预定轨道，这种控制需要有较高的精度才能完成[2].从国内外的文献来看，轨迹设计的问题需要进行合理的优化才能解决，这样才能满足飞行器飞行过程中的各种约束及入轨时的各种指标[3-4].

高超声速飞行器在上升段过程中，需要保持纵向平面内有机动且横侧面的机动尽可能的小，本文研究的重点是飞行器在纵向平面内的轨迹设计问题，因此忽略飞行器在横侧面的机动，认为飞行器只在纵向平面内机动.因此，高超声速飞行器的动力学模型如下[5].

(1)

模型补充:推力P不可调并且平均为180 kN，发动机工作时间为65 s.使用杨炳尉大气模型.

2 上升段轨迹优化设计

2.1 最优控制模型

建立关于飞行器上升段轨迹设计的最优模型，具体如下.其中控制量为攻角α，状态变量为V,x,y,m,θ,分别为飞行器速度、飞行距离、飞行高度、飞行器质量以及轨迹倾角.

1)以飞行器总吸热量为性能指标函数，如下所示:

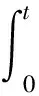
(2)

2)状态方程如公式(1)所示.

3)采用攻角作为最优控制量.

4)初始状态取飞行器垂直上升段的末状态.

5)约束条件如下：

控制量约束(攻角约束)

αmin≤α≤αmax

(3)

法向过载约束

(4)

热流约束

H≤Hmax

(5)

动压约束

(6)

终端状态约束

θ(tf)=θT

Vmin T≤V(tf)≤Vmax T

αmin T≤α(tf)≤αmax T

(7)

其中：tf为飞行器飞行结束时刻.

2.2 模型转换

从上面的最优控制模型能够看出，高超声速飞行器的上升段轨迹优化的问题，能够看作最优控制问题中终端不固定的分类，也就是飞行器达到终端状态时的飞行结束时间相对不固定.对于这种问题，直接对其求解有一定的难度，因此需要对模型进行合适的变化，转换为终端固定问题从而使求解过程简易化.

取变量τ，令τ=t/tf，t为飞行器飞行过程中的当前时刻，tf为飞行器达到飞行终端状态的时刻，τ∈[0,1].令τ为状态方程的自变量，则对应的积分区间变成[0,1]，使原优化问题变为了终端固定的问题，终端飞行时间tf可视为一个待优化的参量.

性能指标：

大脑坡矿区位于花垣—张家界断裂带南东侧、民乐—李梅背斜近核部之南东翼，区内出露的地层有寒武系石牌组、清虚洞组、高台组、娄山关组及第四系等。为一倾向南东的单斜构造，断裂中等发育，无岩浆岩分布，未见明显变质为基本特征（见图1）。

(8)

状态方程：

(9)

与攻角相关的参数为控制变量，u=[u1,u2…uM]，这些参数的个数和形式由参数化方法决定.

初始状态取垂直上升段的末状态.

约束条件：

要满足非线性规划方法的要求，须将各约束条件全部离散化至离散点处.若将飞行时间区间[t0,tf]等分为N段，将约束条件离散化到每一节点处，例如攻角约束离散为：

αmin≤α0≤αmax

┇

αmin≤αN≤αmax

(10)

其他约束按上述规律依次类推.

得到上述非线性规划模型，运用序列二次规划算法，便可进行轨迹设计及优化的工作.

3 轨迹优化仿真

最优控制类问题转化为非线性规划类问题，关键是合理的参数化.参数化就是用将原来的控制变量用几个参数表示，把对原控制变量的优化问题转化为了对这些参数的优化问题.本文采用了以下参数化方法用以解决问题.

将控制变量在时间[0,tf]上离散为若干个节点，节点与节点之间用多项式来近似.把[0,tf]等分为N段，则最优控制变量α*可表示成[α0,α1,α2,…αN]，再加上终端飞行时间，对攻角的优化就转变为对[α0,α1,α2,…αn,tf]这N+2个参数的优化.为了避免在优化变为对局部寻找最优，在满足一定精度的前提下，优化的参数不宜选取过多.根据相关资料，仿真过程中选取N=7比较合理.

取约束条件如表1所示.这些约束条件的取值依据主要为高超声速飞行器的总体以及气动方案和一些相关的轨迹计算的工作[6-7].

根据表中约束值进行仿真分析，得到仿真曲线如图1～6所示.

表1约束限制值

过程约束αminαmaxqmaxnymaxHmax数值-126100-1.5600终端约束αmin Tαmax TMαmin TM αmax TθT数值04670.5

图1 攻角变化曲线

图2 马赫数变化曲线

图3 法向过载变化曲线

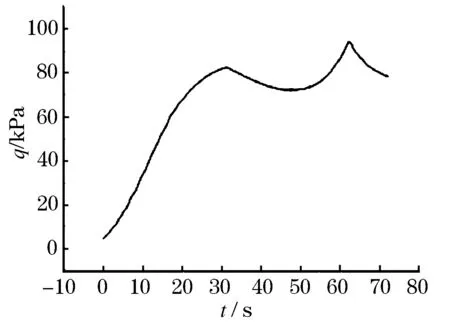
图4 动压变化曲线

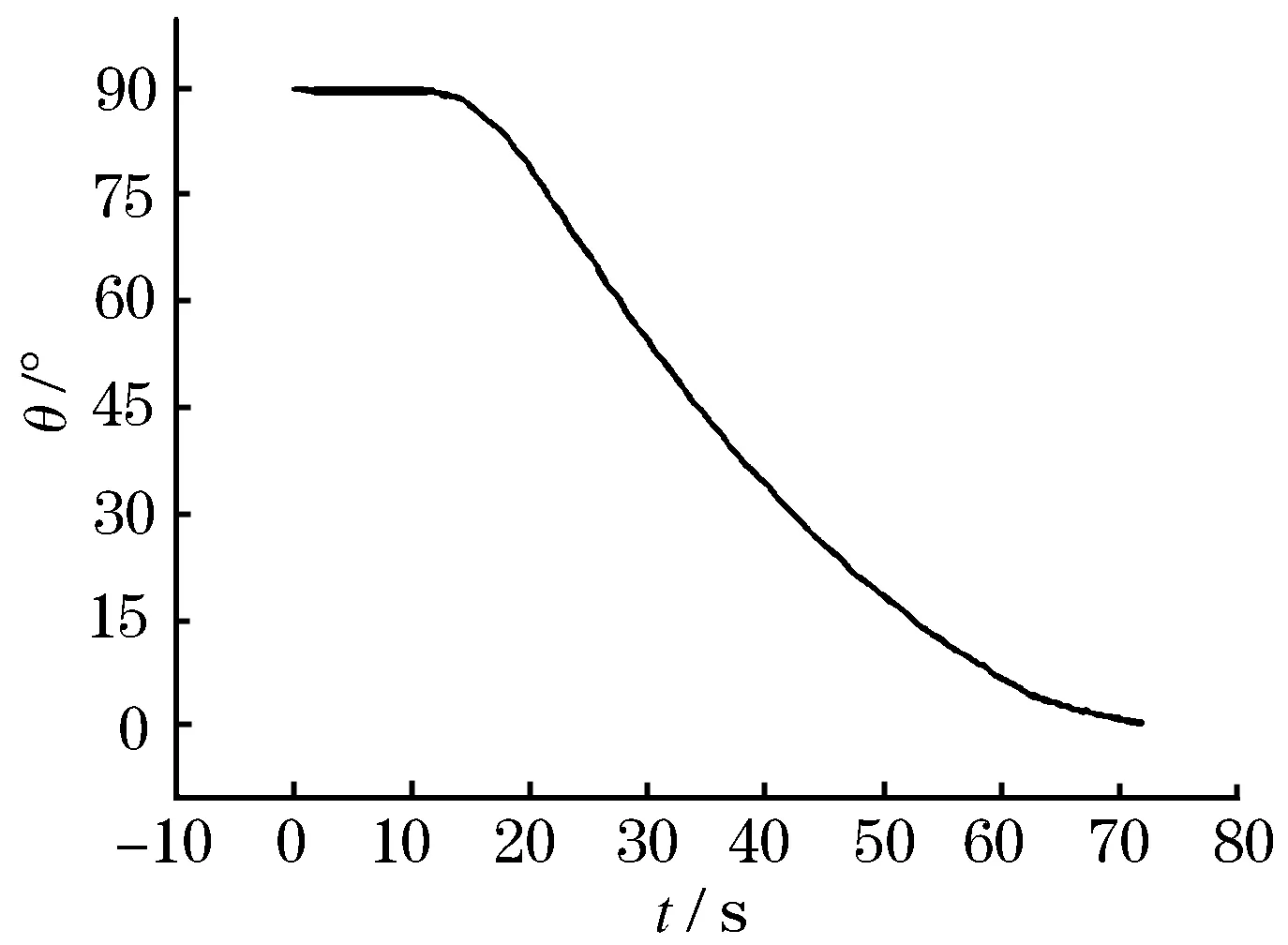
图5 轨迹倾角变化曲线

图6 热流变化曲线

由图1可以看出，攻角在飞行的初始阶段基本保持为0°，这表明在这个阶段飞行器在尽量往高空爬升，因为短时间上升到较高空域，动压以及热流的数值会比较小.之后有将近10 s的负攻角阶段，由于法向过载的严格约束，负攻角的峰值并未达到限制值.从变化曲线来看，飞行器上升段攻角变化在正常范围内.

由图2可以看出，马赫数在上升段持续增长，临近终端飞行时刻时接近限制值并回落至正常值，在终端飞行时刻达到预定的飞行马赫数，符合预想设计.

由图3可以看出，飞行器法向过载峰值出现在20 s左右，注意到20 s左右时，飞行器的负攻角最大，飞行器转平的趋势比较明显，从而受气动力较大，因此引起过载峰值.之后时间内法向过载一直紧贴着限制的边界不停变化，然后攻角却在不断减小，这是由于飞行器马赫数越来越大，动压也一直为增大的趋势，所以较小的攻角也能较大的过载.从变化曲线来看，法向过载约束严格限制了飞行器的法向过载而未达到峰值，属于正常的变化范围内.

由图4可以看出，动压的峰值出现在发动机关机点处，此时飞行器飞行马赫数最大，从而导致动压出现峰值.此时峰值也在限制值范围内，符合设计需求.

由图5可以看出，上升段初始一段时间，轨迹倾角为90°，与攻角的趋势相同.之后随着时间慢慢减小，飞行器机体逐渐转平，在终端时间趋近与0°，整个变化过程符合高超声速飞行器的入轨要求.

由图6可以看到，热流的峰值同样出现在关机点处，此时飞行器的飞行马赫数最大，而马赫数对热流的影响显著，所以出现了峰值，但在约束范围之内，符合要求.

为直观体现约束条件对轨迹的限制作用，给出各约束状态的峰值，见表2.

表2约束限制值与仿真峰值

αqθTnyHMαT约束值[-12,6] 100 0.5 -1.5 600[6,7]峰值-9.53194.60.5-1.55756.5

由表2可见，各个状态变量完全满足飞行器的各项约束条件，而且都能够很精确达到预设定的终端条件.在这组约束条件中，法向过载的约束最为严格，因此，飞行器在大部分飞行时间都沿法向过载约束的边界飞行，这说明这种算法有比较强的边界搜索能力.

4 结 语

本文通过分析高超声速飞行器上升段的飞行特点，通过建立合理的模型，根据其多个方面的飞行约束，并通过优化算法，对飞行器的轨迹进行了仿真验证，结果表明优化设计算法满足多约束条件要求，验证了轨迹设计的合理性.

参考文献：

[1] 李佳峰, 周 浩, 陈万春. 高超声速飞行器滑行段最优弹道的间接算法[J]. 飞行力学, 2009, 27(3):41-44.

[2] 吴德隆,王小军.航天器气动力辅助变轨动力学与最优控制[M]. 北京: 中国宇航出版社, 2006.

[3] 雍恩米. 高超声速滑翔式再入飞行器轨迹优化与制导方法研究[D].长沙: 国防科学技术大学, 2008.

[4] MOSES P L, RAUSCH V L, NGUYEN L T,etal. NASA Hypersonic Flight Demonstrators -overview, Status, and Future Plans[J]. Acta Astronautica, 2004, 55(3-9): 619-630.

[5] 钱杏芳, 林瑞雄, 赵亚男. 导弹飞行力学[M].北京: 北京理工大学出版社, 2011.

[6] 周 浩, 周 韬, 陈万春, 等.高超声速滑翔飞行器引入段弹道优化[J].宇航学报, 2006, 27(5): 970-973.

[7] 李佳峰,陈万春. 带约束的高超声速飞行器最优弹道的数值算法[J].航空学报, 2009, 30(9):1605-1611.