一种改进的RFID标签防碰撞算法
康维新,吴学文, 2
(1. 哈尔滨工程大学 信息与通信工程学院,哈尔滨 150001; 2. 中国人民解放军91899部队,辽宁 葫芦岛 125001)
射频识别(Radio Frequency Identification,RFID)技术即一种自动识别技术,通过无线射频方式进行非接触式双向数据通信,对目标加以识别并获取相关数据,整个识读过程不需要人员参与即可完成信息读写及相关处理,操作简单快捷[1].RFID技术在物品的追踪管理上有很大的优势:非接触式自动识别技术,数据存储容量大、可读写、可重复利用、穿透能力强、读写距离远、读取速度快、环境适应性好、使用寿命长,可以实现多目标识别的自动识别技术[2].
无线射频识别技术最大的特点是非接触式的自动识别,且在阅读器识别范围内实现多目标识别,然而多标签与阅读器同时通信,必然会在无线共享信道上形成相互干扰,致使阅读器不能成功接收电子标签的数据信息,从而产生了电子标签碰撞问题.
1 RFID防碰撞算法
目前,已研究出许多种技术来解决标签防碰撞问题,其中多址技术为标签防碰撞的常见解决方法.该技术主要为空分多址(SDMA)技术、码分多址(CDMA)技术、频分多址(FDMA)技术和时分多址(TDMA)技术.前三种多址技术主要基于硬件的技术,通过改善硬件的条件来解决碰撞问题,但因利用率低、实现成本比较高,所以较少实用[3].目前RFID系统中普遍采用的防碰撞算法主要是基于TDMA思想,TDMA防碰撞算法又可以分为两大类:一类是基于二进制搜索的确定性标签防碰撞算法,一类是基于ALOHA的概率性算法[4].
1.1 ALOHA系列防碰撞算法
纯ALOHA算法(Pure ALOHA PA算法)是最简单的基于ALOHA的标签防碰撞算法,此种算法采取“标签先发言”的方式,即标签一进入阅读器的工作范围就自动向阅读器发该标签的ID.这样,在共享的无线信道内,不同标签的信息传输时间就会有很大概率发生重叠,导致识别的碰撞,碰撞分为完全碰撞和部分碰撞.一旦发生碰撞,阅读器就会命令标签停止发送自身ID信息,该标签会随机的选择回退时间进行重新发送,直到该标签被阅读器识别为止.
时隙ALOHA算法(Slot ALOHA SA算法)是对PA算法的改进,即在原始的PA算法基础上将时间分成若干个时间相等的离散时隙(slot),并且每个时隙的的长度大于标签与阅读器数据交换的时间长度.系统时钟控制时隙长度,并要求各控制单元与系统时钟同步,同时,每个标签必须在时隙起始时刻发送数据信息,因此,标签只会完全接收和完全碰撞两种状态.
帧时隙ALOHA算法(Frame Slot ALOHA FSA算法)是对SA算法的改进,在SA算法的基础之上引入帧的概念,把L个时隙组成一帧,标签在每一帧值范围内随机选择一时隙发送ID数据给阅读器.
动态帧时隙ALOHA算法(Dynamic Frame Slot ALOHA DFSA算法)是对FSA算法的改进.在FSA算法中,帧长L为固定值,当标签逐渐被识别后,未被标签数逐渐变少,或进入识别范围的标签逐渐变多时,上一帧结束后,下一帧中空闲时隙或碰撞时隙必然会增多,这些将严重降低系统的识别效率.DFSA算法为解决此问题,将帧值L的大小根据标签数量的变化进行动态的调整.
由于基于ALOHA的概率性算法采取“标签先发言” 的模式,并且多标签“发言”具有很大的随机性,导致某一标签可能在相当长的一段时间内无法识别,而且在应用中,随着标签数量的扩大,性能将会急剧恶化,出现吞吐量偏低、“饿死”、识别速度缓慢、能量消耗大等缺点[5].
1.2 二进制树系列防碰撞算法
二进制搜索系列算法的实现防碰撞的基础条件为对碰撞比特位得准确定位.由曼彻斯特(Manchester)编码原理可知,信号的上升沿代表逻辑“0”,下降沿代表逻辑“1”,若信号未发生跳变,则认为是该位没有数据,确认该位出现了碰撞[6].因此,Manchester编译码是二进制搜索系列算法的主要编码方式,其监测碰撞位过程如图1所示.
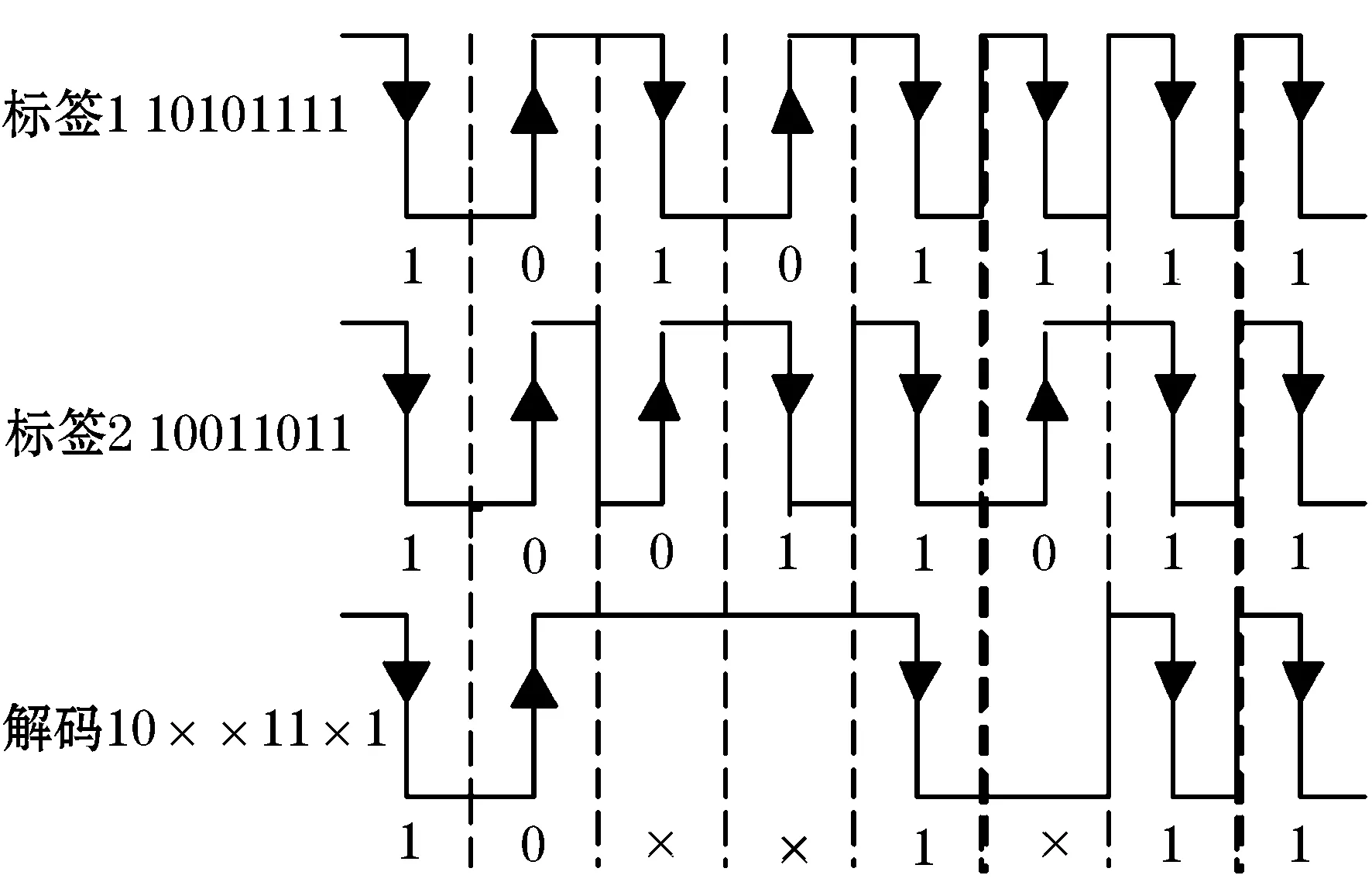
图1 曼彻斯特编码检测碰撞位
二进制搜索算法(Binary Search BS算法)是基于轮询方式,无记忆查询,由多个周期阅读器查询和电子标签应答实现电子标签筛选识别.在每个查询与应答周期内,阅读器发出带比特前缀的查询命令,电子比标签将自身的ID与查询命令进行比较并进行应答.其应答约定为:ID序列小于或者等于查询命令的电子标签进行应答,若识别区域内有两个以上电子标签同时满足应答条件,阅读器判断为标签碰撞.接着阅读器根据发生碰撞的最高比特位,将此位置“0”,该位以后的比特位都置“1”,产生新的查询命令,再进行寻呼,识别出一个电子标签后,阅读器从头开始发送Request(1111……1111)指令,按照上述方式来识别其它的电子标签,直到工作区域内所有的电子标签都被识别出来.二进制搜索算法的命令序列格式:Request(请求命令)—Select(选择命令)—Read_Data(读写数据命令)—Unselect(退出命令)[7].搜索算法本质上就是二叉树的一种遍历形式.假设标签平均每次传送的二进制码的长度为L,int(·)为向上取整,成功识别一个标签的搜索次数为:
S(N)=log2N+1
(1)
总搜索次数S(N)为:
S(N)=int(log2N!+N)
(2)
总通信量LBS为:
LBS=S(N)×L=int(log2N!+N)×L
(3)
动态二进制搜索算法(Dynamic Binary Search DBS算法)是一种改进的BS算法[8].在BS算法中,阅读器寻呼与标签响应的都是传输完整的标签ID号,如果标签ID号很长,所传输的数据量就会非常大,这样就增加了搜索时间和出错频率.实际上,阅读器发送的请求命令中,最高碰撞位以后各位不包含给电子标签的补充信息,因为这些位总是被置“1”,只要事先预定好,这些信息可不必发送.电子标签响应的ID号的 最高碰撞位以前各位不包含给阅读器的补充信息,因为这些位是已知且给定的.若把这些冗余信息剪掉,系统的传输效率会大大提高.因此,DBS算法的每次搜索,阅读器只发送碰撞位之前的比特位信息及碰撞位比特码,标签只回送给阅读器碰撞位之后的比特位,一次搜索传输的信息量正好为一个完整标签的比特位长度L.
总搜索次数S(N)为:
S(N)=int(log2N!+N)
(4)
平均每次传输的比特数为:
(5)
总通信量LDBS为:
(6)
后退式二进制搜索算法(Retreat Binary Search RBS算法)是从减少搜索次数上对BS算法的改进.BS算法与DBS算法每成功识别一个标签之后,都会回到根节点,发送全“1”的最大Request命令.而RBS算法则不同于二者,它成功识别一个标签之后,并不返回根节点,而是返回上次碰撞节点,即父节点[9].
RBS算法的总搜索次数S(N)为:
S(N)=2N-1
(7)
总通信量LRBS为:
LRB=S(N)×L=(2N-1)×L
(8)
BS算法虽然能解决ALOHA算法中的“饿死”问题,但却由于过大的搜索次数及总通信量,使系统识别速度降低,能耗变大,系统的吞吐率最大为左右;DBS算法是在减少通信量的基础上对BS算法的改进,其通信量只有BS算法的,总搜索次数与BS算法相同.RBS算法是在减少总搜索次数基础上对BS算法的改进,其搜索次数较BS、DBS算法有了较大减少,系统的吞吐量维持在左右[10].
2 一种改进的RFID防碰撞算法
2.1 改进算法原理
通过上节对各算法的研究分析,可以看出,要提高防碰撞算法的性能可以从两个方面进行改进,一是减少阅读器与标签的通信次数,即减少搜索次数;二是减少数据传输量,即减少通信的比特长度.本节以二进制搜索算法为基础,采用曼彻斯特编解码机制,结合动态二进制搜索算法和后退二进制算法的优点,提出了一种改进算法.
改进算法命令组:Request (SN):请求(序列号),此命令要求阅读器向进场标签发送一寻呼序列,标签接到命令后将自身序列号与之比对,如果电子标签的ID中包含此前缀序列号,则此电子标签回送其序列号给阅读器.Request (SN,0):锁位查询命令,该命令根据标签查询结果,进行曼彻斯特译码,确定碰撞位后根据取值约定,生成下一轮的寻呼序列号.它的取值约定为:对解码的后的标签序列号进行碰撞位判断,对阅读解码系列的碰撞位置“1”,其余非碰撞位置“0”,从而得到锁定碰撞位的查询命令.阅读器在发送锁位查询命令后,电子标签按位将自身的ID与查询命令中与逻辑“1”对应的比特位锁定提取,生成新的标签ID,以后的查询与应答均是以此ID作为依据.并且此查询命令发送后,只有锁定的最高碰撞位为逻辑“0”的电子标签进行应答,回送值为除了最高锁定位的新ID.Request (SN,1):“1”分支寻呼.针对Request (SN,0)命令,“0”分支识别结束,返回父节点进行寻呼命令.Select(选择命令)、Read_Data(读写数据命令)、Unselect(退出命令)与之前的二进制搜索算法命令一致.
2.2 改进算法流程及实例分析
改进算法的流程如图2所示.
下面以标签A(10110011)、标签B(10100010)、标签C(10110010)、标签D(11100010)进行实例演示分析,具体过程如图3.
2.3 改进的防碰撞算法仿真结果分析
在理想信道条件下,不计控制、前后缀和校验冗余等开销,参考ISO18000-6 标准,进行仿真.标签数量在0~100动态变化,标签ID长度为16位,比特率为100 Kb/s,通过20次仿真取均值,对读写器识别所有标签所用总搜索次数、系统总通信量以及吞吐率等性能指标进行分析,与BS算法、DBS算法、RBS算法进行比较.
图4为阅读器在不同标签下各算法的总搜索次数比较,由于改进算法使用后退二进制搜索算法的返回策略,同时改进算法由于对碰撞位进行锁位处理,这样减少了搜索次数,经过仿真分析,改进算法总搜索次数较其他算法有很大改进;图5为各算法的总通信量比较,由于改进算法采取对碰撞位的锁位处理,每次传输的数据只是对碰撞位进行处理,这样就减少了传输的信息量,通过对比分析,改进算法的总通信量的显著减少,提高了识别的速度;图6为各算法的吞吐率分析,通过仿真分析,改进算法的吞吐率在50%~60%,略高于后退式二进制搜索法,并且随着标签数的增加有显著增大趋势.

图2 改进的防碰撞算法流程图

图3 改进的防碰撞算法操作实例

图4 总搜索次数比较图
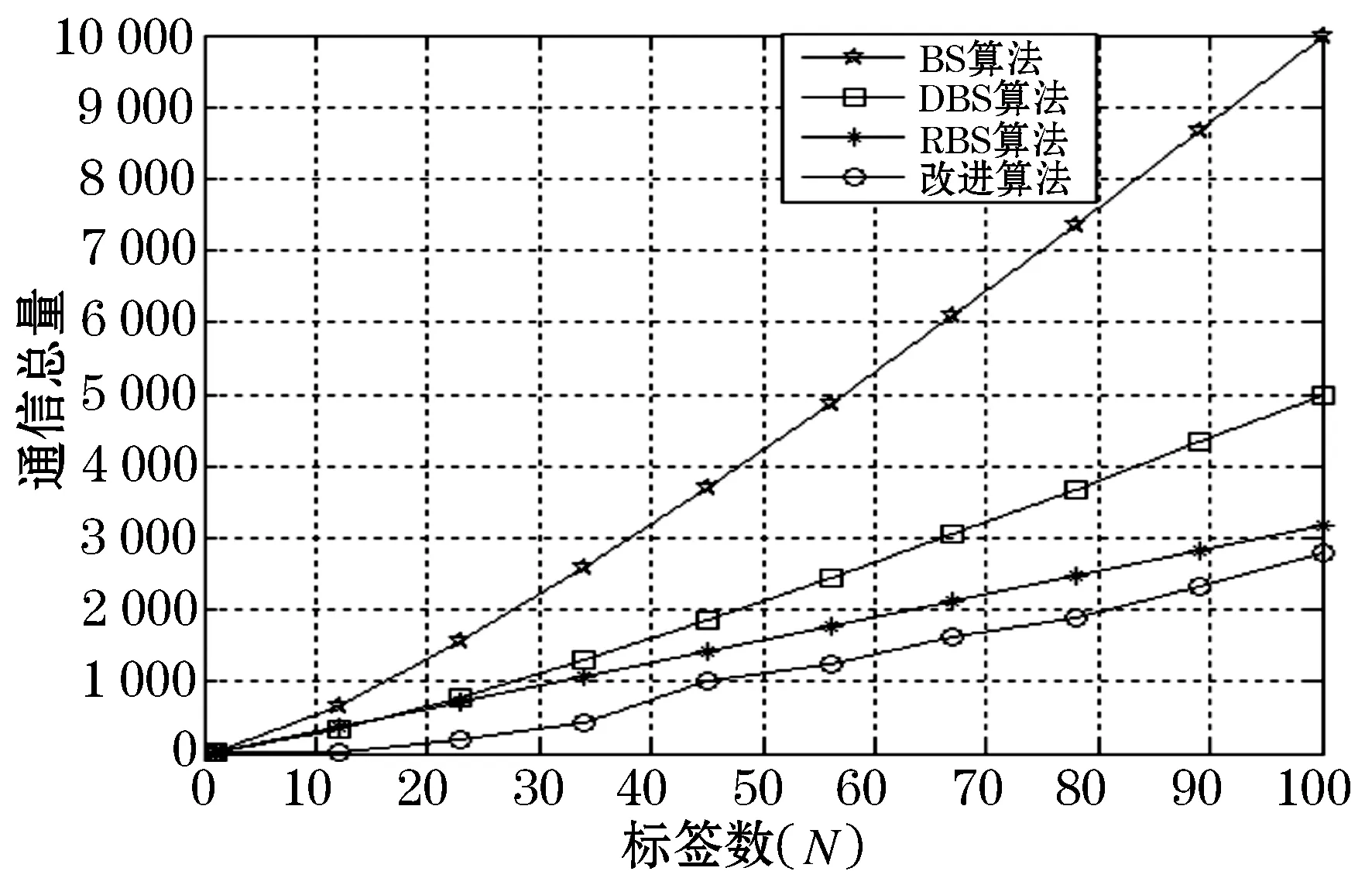
图5 总通信量比较

图6 吞吐率比较
3 结 语
本文分析了当前的防碰撞算法,结合实际应用提出了一种改进的防碰撞算法,该算法以减少搜索次数与减少信息传输量为改进思路,采用了曼彻斯特编解码识别机制,碰撞位锁定机制,后退式二进制搜索算法的后退机制,跳跃二进制搜索算法的碰撞位传输机制四种机制有效的结合,经过仿真分析,验证了算法的可行性,降低了系统的能耗,同时对标签的硬件要求较低,更利于实践应用.
参考文献:
[1] 李全圣, 刘忠立, 吴里江. 特高射频识别技术及应用[M]. 北京: 国防工业出版社, 2010. 275-277.
[2] 徐 卓. 基于RFID的军用物流管理系统的研究与设计[D]. 哈尔滨: 哈尔滨工程大学, 2011. 1-3.
[3] 胡正超. 基于二进制树的RFID防碰撞算法的研究[D].长春: 吉林大学, 2009. 26-28.
[4] 冯 娜, 潘伟杰, 李少波, 等. 基于新颖跳跃式动态搜索的RFID防碰撞算法[J]. 计算机应用, 2012, 32(1): 288 -291.
[5] 王 雪, 钱志鸿, 胡正超, 等. 基于二叉树的 RFID 防碰撞算法的研究[J].通信学报, 2010, 31(6): 49-57.
[6] KLAIR D K, CHIN K W, RAAD R. A survey and tutorial of RFID anti-collision protocols [J]. IEEE Communications Surveys & Tutorials, 2010, 12(3): 400-421.
[7] ZHANG Yan, YANG L T, CHEN Ji-ming. RFID与传感器网络:架构、协议、安全与集成[M]. 北京: 机械工业出版社, 2012. 1-45.
[8] 杨成龙. RFID装备管理系统的防碰撞算法[J].四川兵工学报, 2013, 34(6): 75-78.
[9] 王 珏. RFID防碰撞算法的研究[D]. 南京: 南京邮电大学, 2011. 23-30.
[10] 张文欣,昂志敏,尹夕振. 一种改进的后退式二进制搜索RFID多标签防碰撞算法[J].合肥工业大学学报:自然科学版, 2012, 35(7): 199-221.

