分数Vasicek利率模型下几种新型期权定价

王媛媛，薛 红

(西安工程大学 理学院，西安 710048)

期权定价问题是数理金融学中的核心问题之一. 1973年，Black和Scholes发表了关于期权定价的开创性论文，得出了著名的Black-Scholes模型. 在Black-Scholes模型中，假设股票价格服从几何布朗运动，且利率为常数. 但在实际中，即使是短期利率也是不断变化的，文献[1-3]研究了Vasicek随机利率模型下欧式期权定价问题. 由于股票价格对过去价格具有依赖性，许多文献考虑用分数布朗运动驱动的随机微分方程来刻画股票价格变化[4-7]，同时，因突发事件的影响，股票价格可能会出现“跳跃”，许多学者考虑用Poisson过程和分数布朗运动驱动的随机微分方程来描述股票价格变化，并讨论期权定价问题[8-10].

1998年Bladt和Rydberg首次提出期权定价的保险精算方法[11]，该方法将期权定价的问题转化为公平保费的确定问题. 它不仅对于无套利、均衡、完备的市场有效，且对于有套利、非均衡、不完备的市场也有效. 近年来许多文献应用保险精算的方法讨论期权定价问题[8-13].

本文假定股票价格过程服从分数跳-扩散过程，利率满足Vasicek模型，利用保险精算方法给出了几种新型期权-欧式看涨幂期权、欧式上封顶及下保底看涨幂期权定价公式.

1 具有随机利率的金融市场数学模型

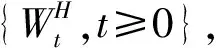
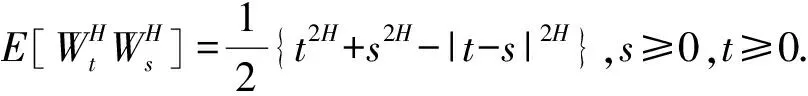
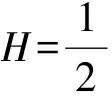
考虑如下模型(A)：股票价格和利率rt满足随机微分方程

(1)

(2)

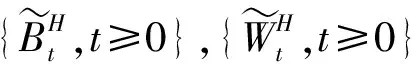
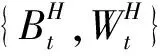
(3)

(4)

引理1[14]随机微分方程(3)的解为

(5)

引理2[8]随机微分方程(4)的解为

(6)

定义2[8]价格过程{St,t≥0}在[t,T]时间段内期望收益率βu满足

(7)

引理3[8,121{St,t>0}在[t,T]上的期望收益率βu满足βu=μu，u∈[t,T].

2 欧式看涨a次幂期权定价

定义3[8]欧式幂期权在t时刻的价值定义为：股票到期日价格按期望收益率折现值的幂与执行价(看作是无风险资产债券)按无风险利率折现值的差在股票实际分布概率测度下的数学期望，这一定价称为期权的保险精算定价. 用C(t,St)表示以股票价格St为标的资产、执行价为K、到期日为T的欧式看涨a次幂期权在t时刻价格，则欧式看涨α次幂期权的保险精算价格

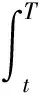
引理4[15]设a，b，c，d，k是实数，并且假设ξ1，ξ2是标准正态随机变量，且有cov{ξ1,ξ2}=ρ，则

其中Φ(·)是标准正态分布函数.

引理5[15]设a，b，c，d,k是实数，并且假设ξ1，ξ2，ξ3是标准正态随机变量，且有

cov(ξ1，ξ3)=ρ,cov(ξ1，ξ2)=0，cov(ξ2，ξ3)=0，

则有

E[exp{aξ1+bξ2}Iaξ1+bξ2+cξ3≥k}]=

定理1 假设股票价格满足随机微分方程(4)，利率满足随机微分方程(3)，则执行价为K、到期日为T的欧式看涨α次幂期权在t时刻保险精算价格

(8)

其中：Φ(·)是标准正态分布函数，且

D1=α2(1-δ2)σ2(T2H-t2H)，

D2=a2δ2σ2(T2H-t2H) ,

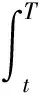
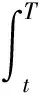
证明令

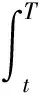
由引理1、引理2、引理3，有

由Ito积分可得

令

所以

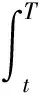
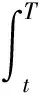
从而

注1 当b=0,c=0,a→0时，可得利率为常数且股票价格服从分数跳-扩散过程情形下欧式看涨α次幂期权定价公式

其中Φ(·)是标准正态分布函数，且

特别地，当λ=0，Ui=0，(i=1,2,…)时，可得分数布朗运动下欧式看涨α次幂期权定价公式(见文献[7]).

注2 当α=1时，可得利率服从Vasicek模型且股票价格服从分数跳-扩散过程情形下欧式看涨期权定价公式(见文献[16-17]).

3 欧式上封顶与下保底次幂期权定价

定理2 假设股票价格满足随机微分方程(4)，利率满足随机微分方程(3)，则执行价为K、到期日为T、上封顶价格为L1的欧式看涨上封顶α次幂期权在t时刻保险精算价格

证明欧式看涨上封顶次幂期权的保险精算价格

类似定理1证明可得结果.

定理3 假设股票价格满足随机微分方程(4)，利率满足随机微分方程(3)，则执行价为K、到期日为T、下保底价格为L2的欧式看涨下保底α次幂期权在t时刻保险精算价格

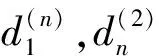
证明欧式看涨下保底次幂期权的保险精算价格

类似定理1证明可得结果.

注3 令定理2中的L2=+∞，或定理3中的L2=0，可得定理1的结果.

注4 当b=0，c=0,a→0时，可得利率为常数且股票价格服从分数跳-扩散过程的欧式看涨上封顶次幂期权和欧式看涨下保底α次幂期权的定价公式(见文献[8]).

参考文献：

[1] 王莉君, 张曙光. 随机利率下重置期权的定价问题[J ]. 高校应用数学学报A辑, 2002, 17 (4) : 471-478.

[2] 刘 坚, 杨向群, 颜李朝. 随机利率和随机寿命下的欧式未定权益定价[J]. 广西师范大学学报：自然科学版 , 2005, 23 (4) : 49-52.

[3] 刘敬伟. Vasicek随机利率模型下指数O-U过程的幂型期权鞅定价[J]. 数学的实践与认识, 2009, 39(1): 31-39.

[4] 薛 红, 王拉省. 分数布朗运动环境中最值期权定价[J]. 工程数学学报, 2008, 25(5): 843-850.

[5] ELLIOTT R J, HOEK J. A general fractional white noise theory and applications to finance [J]. 2003, 13(2): 301-330.

[6] BIAGINI F, HU Y, KSENDAL B,etal. Stochastic calculus for fractional brownian motion and applications [M]. New York: Springer, 2008.

[7] 刘海媛, 周圣武, 索丽娟. 标的资产服从分数布朗运动的几种新型期权定价模型[J]. 数学的实践与认识, 2008, 38(15): 54-59.

[8] 薛 红, 孙玉东. 分数跳-扩散环境下几种新型期权定价模型[J]. 数学的实践与认识, 2012, 42(24): 132-140.

[9] 隋梅真, 张元庆. 分数布朗运动和泊松过程共同驱动下的欧式期权定价[J]. 山东建筑大学学报. 2008, 23(1): 70-73.

[10] 赵建国，师 恪. 股票价格服从分数跳-扩散过程的期权定价模型[J]. 新疆大学学报:自然科学版, 2006, 23(2): 166-169.

[11] BLADT M T, RYDBERG H. An actuarial approach to option pricing under the physical measure and without market assumptions [J]. Insurance: Mathematics and Economics, 1998, 22(1): 65-73.

[12] 闫海峰, 刘三阳. 广义Black-Scholes模型期权定价新方法[J]. 应用数学与力学. 2003, 24(7): 730-738.

[13] 黄开元，薛 红. 分数跳-扩散过程下双标型两值期权定价模型[J]. 宁夏大学学报：自然科学版, 2013, 34(2): 105-108.

[14] 薛 红, 李小军, 吴晓蕊. 随机利率下可转换债券定价[J]. 西安工程大学学报, 2011, 25(1): 109-121.

[15] CHEN S. Financial engineering [M]. Shang Hai: Fudan University Press, 2002.

[16] XUE H, LU J X, LI Q Y,etal. Fractional jump-diffusion pricing model under stochastic interest rate[C]//IACSIT Press: 2011 3rd International Conference on Information and Financial Engineering, 2011. 428-432.

[17] 杨淑彩，薛 红，王晓东.具有随机利率的分数型复合期权定价横型[J].哈尔滨商业大学学报：自然科学版，2014,30(1):97-102.