双参数C0半群的谱映射定理
赵 拓, 赵华新, 徐 敏
(延安大学 数学与计算机科学学院,陕西 延安 716000)
在经典算子半群理论中,谱映射定理是其非常重要的组成部分,文献[1]给出了C0半群的谱的概念和谱映射定理;文献[2]定义了C半群的谱及其与生成元谱之间的关系;文献[3]给出了C半群的谱映射定理;文献[4-5]研究了可微C半群和广义C0半群的谱映射定理;文献[6]研究了双参数C0半群生成元的一些性质及其预解式;文献[7]研究了C半群的指数公式,并将其推广到双参数C半群上;文献[8]定义了双参数C半群及其收敛性.基于以上的研究,本文将单参数C0半群的谱及其谱映射定理推广到双参数C0半群上,给出了双参数C0半群谱的定义及谱映射定理.
本文中X均为复Banach空间,I为恒等算子,A为算子半群在Banach空间中的无穷小生成元.
1 基本概念与引理
定义1设{T(s,t)}s,t≥0是(A1,A2)生成的双参数C0半群,称集合
{aλ+bμ|((aλ+bμ)-T(s,t))-1∈B(X),a,b,λ,μ∈R}
为{T(s,t)}s,t≥0的预解集,记作ρ(T(s,t)),称集合Cρ(T(s,t))为双参数C0半群{T(s,t)}s,t≥0的谱,记作σ(T(s,t)).
定义2[2]设{T(s,t)}s,t≥0为复Banach空间X上的双参数C0半群,
1) 若((λa+μb)-T(s,t))-1不存在,则称(λa+μb)为{T(s,t)}s,t≥0的点谱,记作σp(T(s,t)).
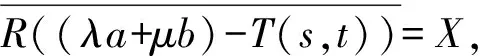
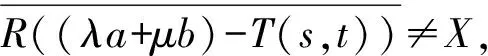
引理1[3]设{T(t)}t≥0为复Banach空间X上由A生成的C0半群,则σ(T(t))⊇etσ(A).
2 主要结论
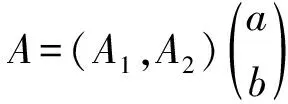
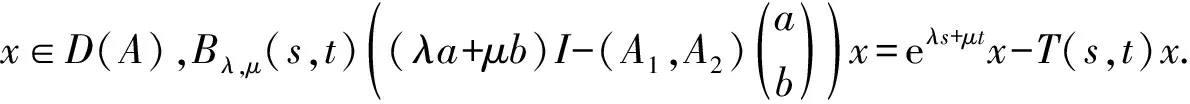
证对任意λ,μ∈R,由Bλ,μ(s,t)的定义可知Bλ,μ(s,t)∈Β(X),对∀x∈X,有
因为
=T(s,t)x,
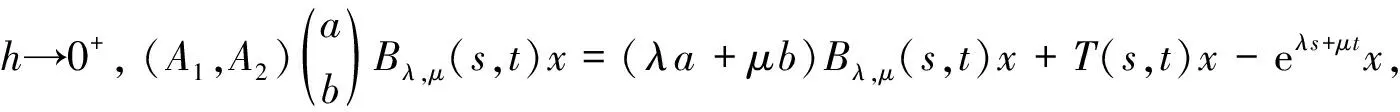
(1)
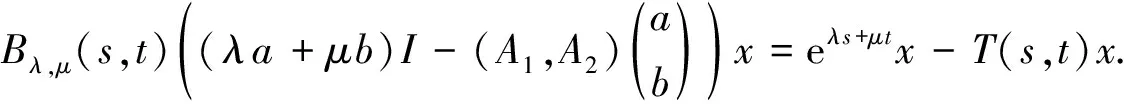
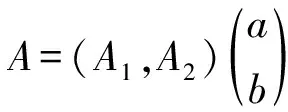
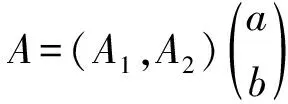
⊇{(λa+μb)|eλa+μb∈ρ(T(s,t)),a,b,λ,μ∈R}.
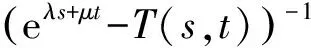
对于∀x∈D(A),有
由Bλ,μ(s,t)的定义知Q与Bλ,μ(s,t)可交换,即对∀x∈D(A),有
综上可知
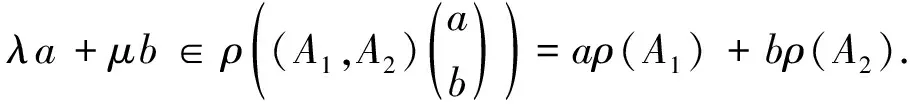
结论得证.
由定义2可知谱分为互不相交的3个部分,分别为点谱、连续谱、剩余谱.
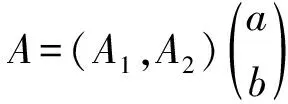
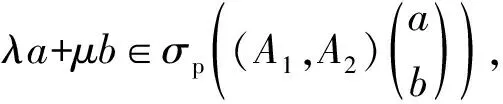
2) 若eλs+μt∈σp(T(s,t)),则∃k∈N,使得
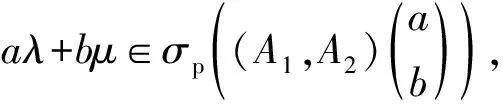
2. 引导质疑 读到这里,你有什么问题?(是什么原因让我理解了爱如茉莉的意思?“我”究竟经历了什么事情?)
由定理1知
即∃x0≠0,使得eλs+μtx0-T(s,t)x0=0,由定义2得eλs+μt∈σp(T(s,t)).
2) 设eλs+μt∈σp(T(s,t)),由定义2,∃x0≠0,使得eλs+μtx0-T(s,t)x0=0,又
e-(λa+μb)(l+t)T(a(l+t),b(l+t))x0=e-(λa+μb)le-(λa+μb)tT(al,bl)T(at,bt)x0=e-(λa+μb)lT(al,bl)x0,
所以连续函数l→e-(λa+μb)lT(al,bl)x0是以t为周期的周期函数,因为e-(λa+μb)lT(al,bl)x0不恒等于零,所以其Fourier系数必有一个不为零,从而∃k∈N,使得
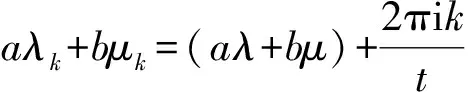
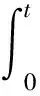
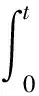
且
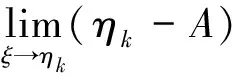
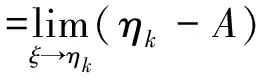
=0,
所以(ηk-A)xk=0,xk≠0,A是闭线性算子,因此
结论得证.
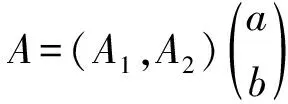
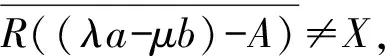
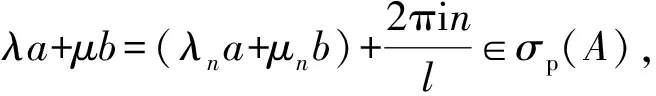
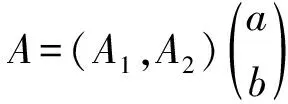
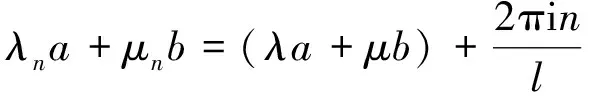
则eλs+μt∈σc(T(s,t)).
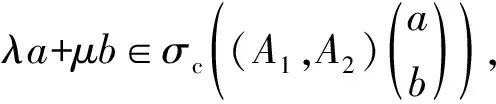
参考文献:
[1] Pazy A.Semigroups of linear operators and applications to partial differential equations[M].New York:Springer-Verlag,1983.
[2] 杜省权,刘清荣.C半群的谱与其生成元谱之间的关系[J].纯粹数学与应用数学,1995,11(1):56.
[3] Song Xiaoqiu.Spectral mapping theorems forCsemi-groups[J].J Math Res Exposition,1996,16(4):527.
[4] 赵华新.可微C0半群的谱[J].天津师范大学学报:自然科学版,2011,31(1):29.
[5] 高文华,卜春霞.广义C0半群的谱映射定理[J].郑州大学学报:自然科学版,2001,33(2):22.
[6] Sharif A S,Khalil R.On the generator of two parameter semi-groups[J].Appl Math Comput,2004,156(2):403.
[7] 赵华新,赵拓,徐敏.双参数C半群的指数公式[J].江苏师范大学学报:自然科学版,2014,32(1):44
[8] 许强.关于双参数C半群的一些结果[J].河南科学,2012,30(11):1564.

