基于模糊聚类分析的木材缺陷CT图像分割

王丽艳，戚大伟

(东北林业大学 理学院，黑龙江 哈尔滨 150040)

木材是人们生产生活中不可缺少的物质资料。但是木材生长周期长，得不到及时的供给，增加了供需矛盾。而人们不合理的利用木材，更加剧了供需矛盾。为了更好的保护森林资源，节约能源[1]，木材缺陷检测有很大的价值。对木材缺陷CT图像的处理也是方法之一。木材缺陷CT图像分割的方法有很多种，实质都是将目标与背景分离，即将缺陷与背景分离[2]。由于事物之间具有或多或少的相似性即产生了模糊现象，给图像分割带来了困难。利用模糊数学聚类的图像分割方法就应运而生。而模糊C均值(Fuzzy C-Means,FCB)聚类算法是当今比较流行的一种算法[3]。它的特点是不需要有先知经验就可以将图像分割成几类，是一种无监督的聚类算法。它以这种强大的优势应用到生活的各个领域，例如医院、气象、经济管理等领域。

但是模糊C均值聚类算法并非十全十美，有很多问题需要改善。主要分为两大方面：一是图像分割过程中，模糊C均值算法各项参数的选择。二是模糊C均值算法对噪声敏感，分割图像时，不能完整的保留边缘细节，丢失很多信息。针对以上问题，许多学者从不同角度对算法进行改进。本文主要是针对模糊C均值算法各项参数的选择问题进行研究。

采用图论的图像分割算法[4]首先分析图像在不同FRFT域的能量分布特点，通过归一化剩余误差因子评估和分析图像所包含的信息，在采用最小生成树的方法对图像区域进行分割。还有很多快速分割方法[5]，将图像数据划分成一定数量的子集，然后利用区域粗糙度标记所有子集，最后根据子集质心及其权重进行模糊聚类图像分割。这两种方法都是先将图像预先分割成几个区域，然后在通过一个适合的方法在将这几个区域在分类。对于木材缺陷CT图像，本文希望将其缺陷例如节子、空洞、腐朽、裂纹等从背景中分割出来[6]。这些缺陷在木材缺陷CT图像中已经自然形成几类。针对木材缺陷CT图像，我们采用半模糊聚类方法对其进行分割[7]。

1 模糊C-均值算法

聚类也就是分类，即把相似的事物归到一类。在现实生活中事物之间没有明显的界限，在某些方面上它们之间因为具有相似的特征，使得它们之间存在着联系[9]。模糊聚类分析是比较流行的分割方法。而模糊C均值聚类算法是模糊聚类经典代表。假设在数据集X中，有n个样本，即n个单元，可有如下表示：Xk(k=0，1，…n-1)。而聚类问题的目的是把{X0，X1…，Xn-1}这个X数据集，分成c(2≤c≤n)个子集，要求相似的样本应尽量在同一子集(聚类)内，c为聚类数目。其原则是：较为相像的样本应归纳到同一个区域，C则为子集个数，聚类的数量。

以往的聚类分析太过于死板，只能将分割好的块严苛的归类到某一区域，使之变成具有这一区域的块的性质，事实上，好多模块的性能并不能从一而论，它会具有好多好多特性，严格的分类反而会降低分析的效果，如果引用模糊聚类的方法，问题就解决了.模糊聚类分析的处理方法为；：假如将所有的数据都规整到C类里，挑X中的其中一个子模块Xk(k=0，1，2，…n-1)，针对一于另一类i(i=0，1，2…c-1)，则可得到μik(0≤μik≤1)，得到的这个数据库则可组成一个模糊聚类数据库，可称作模糊聚类矩阵，其具备的性质如下：

(1)

模糊C均值聚类之所以能得到大家的一致认可，是因为它具有其他聚类分析方法所没有的优良性能，FCM具有很多智能的特性，比如清晰明了的叙述，将分割好的图像自动划分结合。FCM聚类算法的提出者是J.C.Bezdek，他定义了这种算法的函数，即模糊目标函数法，其函数J(U，V)是：

(2)

式中：(Uik)(i=0，1，…c-1；k=0，1，…n-1)为模糊聚类矩阵，且满足式(1)；V={V0，V1，V2，…Vc-1}为C个聚类中心的集合，且Vi∈Rp；m∈[2,∞]为加权指数；dik为第k个样本到第i类的距离，其定义为

(dik)2=‖Xk-Vi‖2(Xk-Vi)T(Xk-Vi)。

(3)

这里Xk为数据样本，且Xk∈RP;T表示矩阵转置；‖·‖为范数，表示欧几里得距离。

如果想要分类得到的结果使人满意，就要选择适合的聚类原则和条件。而模糊C均值算法是通过不断优化目标函数来实现的。目标函数表示为J(U，V)，加权指数是区域子集Xk对第i类隶属度μik的m次方。Bezdek提出加权指数在1.1≤m≤5范围内推广，后来给出经验范围是m=2时最合适[12]。把聚类的条件设置为求目标函数J(U,V)的最小值minJ(U，V)。迭代方案如下：

(1)先将聚类数目C(2≤c≤n)与加权指数m(m∈[2,∞])确定好。

(2)确定模糊聚类矩阵的初始值ul=[uik]l，取l=0。

(3)由以上两步可得到各类的聚类中心Vi的函数式：

(4)

(4)按照下面方法计算新的模糊聚类矩阵u(l)=(l=l+1)

Ik={i0≤i≤c；dik=‖Xk-Vi‖=0}，

(5)检查‖U(l-1)-U(l)‖是否小于预先设定的阈值。如果小于，则停止，否则转至(3)步骤。其任务是确定‖U(l-1)-U(l)‖与先前确定的限值的大小，小于限值则不用继续，如果大于则返回到(3)步骤。

FCM迭代算法结束后，将阀值设为α，那么图像分割的函数，看以下公式uik=max{u0k,u1k,…uc-1k}≥α，则Xk∈第i类图像分割，这是大区域内的数据归纳范畴，FCM算法也有其限制性，究其原因，是因为运算太过复杂的缘故，因为迭代的算法要反复的计算聚类中心及隶属度矩阵[10]，所以此方法未能极大限度的应用。

2 ESFCM 分割算法

(1)假设要分割的图像为f(rk,ck)，图像所对应的任一坐标点为(rk,ck)，那么函数Xk=f(rk,ck)代表图像在这个点处的特征向量，如果图像分割时设定的向量为S个，

设E0为图像中所有非“边缘”点的区域集，E1为所有“边缘”点的区域集，那么E0={Xk|E(rk,ck)=1,Xk∈X}，且X=E0∪E1。

(2)已进行了边缘检测，接着便是分割“边缘”部分，使之形成独立的互补链接的个体，然后“边缘”部分的这些独立个体便智能的分到相近的区域，也就是物理学中的就近法则，从而形成的互相独立而又连接不断的子图，这样初次的图像分割就成功了。

(4)以(2)和(3)给出的数据为基础，将其设定为模糊迭代的最初值，加以迭代计算，迭代时的隶属度

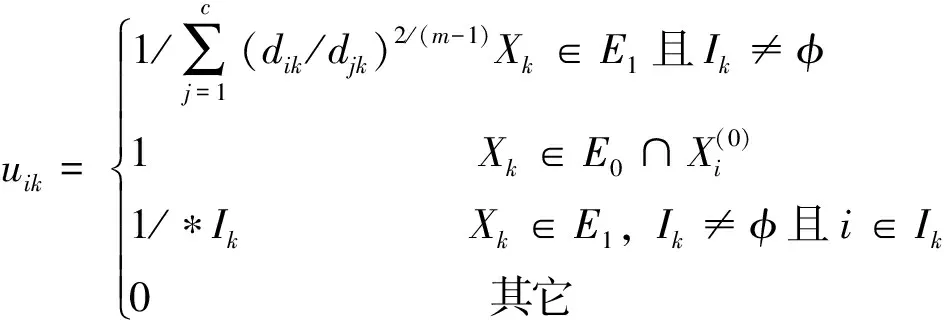
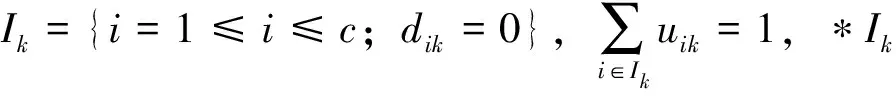
只有在隶属度公式中点Xk∈E1为“边缘”点时，其计算公式才能与普通的FCM相吻合，其采用的是模糊化隶属关系的方法；

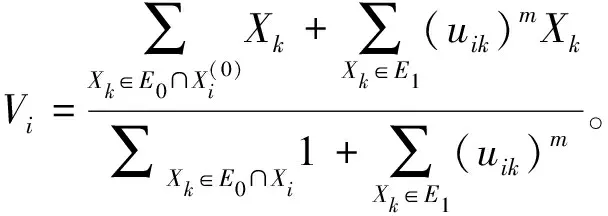
(5)

(5)当以上4个步骤都顺利的完成后，每一个像素的位置将被固定，就终止了迭代。终止迭代也是有相应的条件和方法的，有两种是被广泛应用的：第一，设定某个阀值为上限，控制两代原型的变化范围在其以内。第二，设定某个阀值，使归整的矩形变化范围在其之内。

3 木材缺陷CT图像预处理

(1)图像分割的正确性是否高，关键取决于其是否具有抗外力的能力，在图像分割的操作中，无论是检测还是迭代都很容易受噪声的干扰，以至于影响分割的准确性，因此本文则主张用中值滤波[11]的方案。

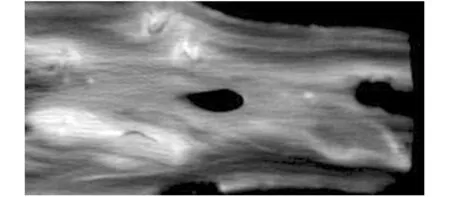
图1 去噪处理后的木材缺陷灰度图像

(2)灰度图像的边缘检测。本文提到的此边缘检测并非是以得到精确的边缘图像为目的，只是作为得到聚类用的最初数据，为下一步得到更精确的图像做铺垫，至于边缘的尺寸和形状可先忽略。下面的边缘图像，是由Robert这种算子检测后得到的。优点是保留更多的信息[8]。

图2 利用Robert算子边缘检测的木材缺陷图像

图3 利用区域生长算法预分割的木材缺陷图像

(3)ESFCM聚类迭代。针对灰度图像来说，设图像的区域集为X={X1，X2，…，Xn}⊂R是在特征向量区域R中的一个有值的区域集(包含多重集合的可能)，因为Xk=f(rk,ck)代表的是第k个点(rk,ck)的灰度值，因此在ESFCM算法中，其目标函数(2)可简单表示为：

(6)

在上述函数中，c可视为ESFCM算法类别数得初始值，那么聚类核心v=(V1,V2,…Vc)也可看作一个C特征向量，Dik可视为是点到类的物理距离D(p,Xj)=Min{d(p,q)|q∈Xj}其中d(p,q)为点p到点q的欧式距离[11]。

图4 经ESFCM处理的木材缺陷图像

4 结 论

本文以含有缺陷的木材为研究对象，利用半模糊聚类算法进行木材缺陷边缘检测，首先对木材缺陷CT图像进行预处理，解决了聚类参数不好确定等问题，利用区域生长法将这些区域又重新分类。实验结果可知：木材缺陷CT图像的缺陷中的节子和空洞边缘连续、平滑，这样就保留了更多的细节。通过这样的方式使图像缺陷分割出来，并且取得理想的效果。

【参 考 文 献】

[1]朴顺姬，戚大伟，金雪蜻.多尺度分形特征在木材内部缺陷检测中的应用[J].森林工程，2012，28(5)：56-59

[2]张德丰.MATLAB数字图像处理[M].北京：机械工业出版社，2012

[3]谢季坚，刘承平.模糊数学方法及应用[M].武汉：华中科技大学出版社，2008

[4]张建梅，孙志田，余秀萍.基于图论的图像分割算法仿真研究[J].计算机仿真，2011，28(12)：268-271.

[5]孙艺峰，王向阳，王春花.一种新的快速模糊C均值聚类图像分割算法[J].小型微型计算机系统，2008，29(2)：320-323.

[6]戚大伟，李 莉.基于分形维数特征的原木漏节图像的研究[J].森林工程，2007，23(5)：11-14

[7]张爱华.基于模糊聚类分析的图像分割技术研究[D].武汉：华中科技大学，2004

[8]韩书霞，戚大伟，于 雷.基于多重分形理论的原木CT腐朽图像分析与处理[J].森林工程，2007，23(5)：15-18

[9]李永生.基于模糊理论的木材X射线图像分析与处理[D].哈尔滨：东北林业大学，2009

[10]范九伦，吴成茂.FCM算法中隶属度的新解释及其应用[J].电子学报，2004，32(2)：350-352.

[11]唐权华，周 艳，金炜东.中值滤波算法的研究与改进[J].微计算机信息，2008，24(8)：187-189.

[12]王黎明.自适应加权空间信息的FCM医学图像分割[J].微型机与应用，2011，30(22)：42-45.