桥式起重机吊重偏摆系统的动力学仿真
薛 伟,万 雷
(东北林业大学 工程技术学院,哈尔滨 150040)
桥式起重机采用钢丝绳连接起重小车和吊装的重物,这种柔性连接方式一方面减少了起升时的冲击载荷,另一方面,由于惯性的影响,吊重在横向搬运时的速度与起重小车的速度不同步,使得吊重在钢丝绳末端做小幅度球面摆动,摆动过程从大、小车的加速起动阶段到稳定运行阶段再到减速制动阶段持续进行,吊重的摆动进而影响了大、小车运行的速度特性。吊重摆动角度的控制和起重小车的准确定位是一个关乎生产安全和生产效率的问题,而对吊摆系统振动特性的研究是对其控制方案设计的基础和参照。
针对吊摆系统的代表性研究中,钟斌将吊摆系统简化为二维质点系运动,采用矢量力学建立了系统的数学模型[1];薛伟应用拉格朗日方程建立了吊摆系统的4自由度动力学分析模型[2],首次考虑了吊重的长度对摆动的影响并引入“质杆”作为其中一个研究对象;Lee在建模基础上,分别采用模糊控制和神经网络控制两种方法进行防摆控制[3];杜文正针对小车位移特性和吊重摆角特性分别设计了两个PID控制器[4]。
1 吊摆系统的动力学模型
1.1 模型建立的基本假设
对吊摆系统做以下3个基本假设作为建模的必要条件:
(1)小车和吊重分别简化为质点O和A,质量分别为M和m,不计吊重的水平扭转。
(2)钢丝绳有足够的强度和刚度,忽略钢丝绳因受力而引起的微小形变。
(3)忽略钢丝绳的质量以及钢丝绳和滑轮组之间的摩擦。
1.2 吊摆系统动力学模型的建立
文献[5]研究表明,吊重在钢丝绳末端做的小幅度球面摆动可以看作分别在大车和小车运行方向上做类似单摆运动的合成。在微摆条件下,某一方向上的摆角只与该方向上的速度特性和该平面内摆动阻尼有关而与其他方向上的因素无关。由于大、小车对各自运动平面内摆角的影响规律相同,且复合运动的研究较复杂,这里假设大车停止,只选择吊摆系统在平面XOZ内的运动作为研究对象,研究转化为3自由度平面运动问题。
起重机工作时,水平搬运和竖直起吊两过程不同时进行,竖直起吊时小车制动,摆角近似为0[6],故本文只研究水平搬运过程。吊摆系统模型如图1所示。

图1 吊摆系统模型示意图
建立坐标系XOZ,其中:小车起始位置为坐标原点O,X和Z两个轴向分别代表小车运行和吊重升降的方向,OB为铅垂线,OA为绳长(摆线长度),∠AOB为摆线与铅垂线二维夹角。记∠AOB=θ,OA=l,吊摆系统的模型如图1所示。
设小车质心坐标(XM,ZM)=(x,0),则吊重质心坐标(Xm,Zm)=(x+lsinθ,-lcosθ)。
小车和吊重的速度分量分别是它们位置坐标的一阶导数:
在忽略掉一些次要因素并做出必要的假设后,起重机吊摆系统就是一个典型的动力学系统。在分析这类小幅度振动问题时,可以用质点系的动能、势能和广义力之类的纯量来描述总体系,本论文采用拉格朗日方程来建立起重机吊摆系统的数学模型。
拉格朗日方程的一般形式如下:
(1)
式中:L为拉格朗日函数,L=T-V,T为系统的动能;V为系统的势能;qj为广义坐标;Qj为广义力。

吊摆系统的动能:
(2)
吊摆系统的重力势能:
V=-mglcosθ。
(3)
拉格朗日函数:
(4)
将(4)式带入(1)式的拉格朗日方程:
(5)
1.3 模型的线性化处理
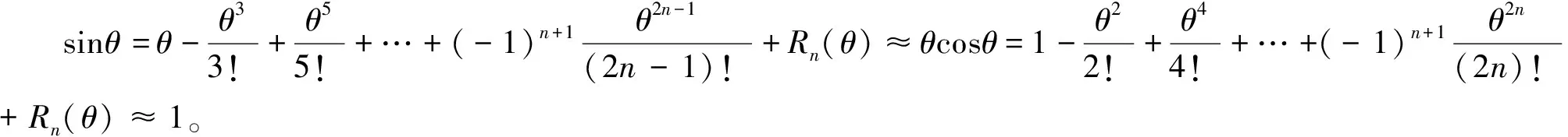
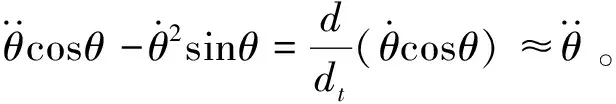
(6)
2 吊摆系统动力学仿真
2.1 仿真的数学模型
(1)小车起停阶段。小车由静止经电动机驱动加速运行到电动机停止驱动后小车被制动最终停止,研究吊摆系统在时域内的变化。由于钢丝绳的摆动阻尼对偏摆运动起抑制作用,故起停阶段忽略钢丝绳阻尼,(6)改写为左端只保留二阶导数的形式(7):
(7)
(8)
2.2 实例仿真
选择QD32/5型号起重机作为实例仿真对象,额定起重量32 t,跨度22 m,最大起升高度13 m,小车质量11.5 t,小车运行电动机YZR160M-1(功率6.3 kW,转速921 r/min),制动器JWZ9-200/E23(制动力矩200 N·m)。应用Matlab/Simulink软件分别对2.1中的公式(1)和公式(2)两阶段的三种工况:①m=25 t,l=10 m;②m=25 t,l=5 m;③m=12.5 t,l=10 m进行仿真。
(1)起停阶段仿真时间12 s,其中电动机驱动8s,制动作用4 s。小车的运动曲线如图2和图3所示,吊重的摆动曲线如图4和图5所示。
(2)制动后吊重的摆动,钢丝绳摆动阻尼600 N·s/m,仿真时间120 s,吊重在不同工况下的摆动角速度如图6和图7所示。

图2 速度—时间曲线图

图3 位移—时间曲线

图4 角速度—时间曲线
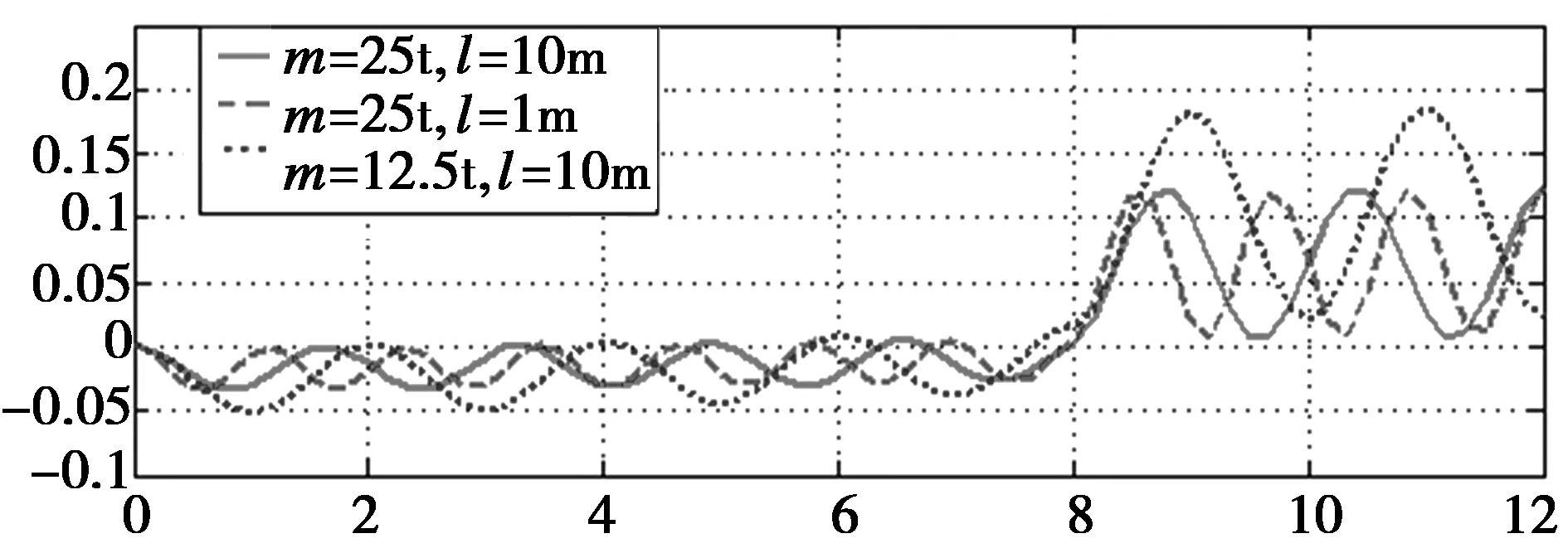
图5 摆角—时间曲线

图6 不同绳长的角速度—时间曲线

图7 不同吊重质量的角速度—时间曲线
3 结 论
结合桥式起重机工作特点,应用分析力学建立了吊重偏摆系统的动力学模型,选取QD32/5型号起重机作为研究对象,采用Matlab/Simulink软件对小车起停阶段和制动后吊重的摆动情况进行仿真,得到了小车的运动特性和吊重的摆动特性。
(1)电动机驱动下,吊重后摆使小车速度呈现加速和匀速的周期性交替变化,3种工况下的周期分别约为1、1和2 s;制动时吊重的前摆程度较大,小车速度整体呈下降趋势的过程中有周期性短暂加速,小车的速度不能稳定。工况①和②的位移曲线基本重合,说明影响小车定位的主要因素是吊重质量,而钢丝绳长度的影响较小。
(2)吊重在电机驱动和制动器制动作用下做受迫摆动,两阶段周期基本相同;3种工况下,起动阶段最大摆角分别为0.03、0.03和0.05 rad;制动阶段最大摆角分别为0.12、0.12和0.18 rad。可见,对吊重系统摆角的控制主要是针对制动阶段。
(3)小车制动停止后,吊重做有阻尼摆动,摆动周期分别为6.8、4.2和4.2 s,摆动完全消除需要的时间较长,都超过120 s。工况①和②的对比说明绳长主要影响摆动周期,缩短绳长可以使摆动周期减小,但增大了约0.2 rad/s的摆动角速度;工况①和③的对比说明吊重质量越小,摆动减弱的越快。
该分析模型和仿真结果接近实际情况,描述的吊运货物时吊摆系统的运动情况,为小车定位控制和吊重的摆动控制提供了基础,具有一定的实际意义。
【参 考 文 献】
[1]钟 斌,程文明,马莉丽,等.起重机小车吊重动力学系统状态空间重构[J].西南交通大学学报,2007,42(4):436-441.
[2]薛 伟,郭永娟.林用起重机起吊木捆偏摆系统的动力学模型与仿真[J].东北林业大学学报,2011,39(6):87-89.
[3]Lee H,Kun C S.A new fuzzy-logic anti-sway control for industrial three-dimensional overhead cranes [A].Proceeding of the 2001 IEEE International Conference on Robotic&Automation [C],2001(5):2956-2961.
[4]杜文正,童国林,强宝民,等.基于模糊自适应PID控制器的桥式起重机定位与防摆控制研究[J].制造业自动化,2012,34(11):8-11.
[5]张则强.桥式起重机吊重二自由度摆角模型与仿真[J].西南交通大学学报,2006,41(6):696-699.
[6]杨会珍,李 虹,赵 勇.门式起重机的减摆PID控制系统[J].起重运输机械,2012(11):16-20.
[7]王玥媛.基于模糊控制的桥式起重机防摆研究[D].大连:大连理工大学,2008.

