基于EMD和自适应提升小波分析的图像增强

李广琼，陈荣元

湖南商学院计算机与信息工程学院，长沙 410205

基于EMD和自适应提升小波分析的图像增强

李广琼，陈荣元

湖南商学院计算机与信息工程学院，长沙 410205

针对经典和提升小波变换共同的缺陷，提出基于EMD和自适应提升小波分析的图像增强算法。对二维图像信息作EMD分解，提取出图像信息的IMF分量，对此IMF分量进行自适应提升小波分解并重构，得到增强图像。仿真及实验结果表明该方法具有有效性和实用性。

提升小波变换；经验模式分解；自适应提升小波变换；图像增强

图像增强[1]是指按照特定的需要突出一幅图像中的目标景物特征，同时去掉不需要的干扰噪声并且提高视觉清晰度的图像处理方法。其目的是能够改善图像质量，提高图像的对比度，突出图像中感兴趣的特征，进而有助于人眼理解或机器识别。目前图像增强的算法主要分为三大类：分别是空域增强方法、频率增强方法[2-3]和基于参数的增强方法[4-6]。基于空域的增强算法处理时直接对图像灰度级做运算，如直方图均衡法，其主要缺陷是增强图像的同时放大了噪声；又如邻域增强算法在消除图像噪声的同时容易引起边缘的模糊。基于频域的增强算法是在图像的某种变换域内对图像的变换系数值进行某种修正，是一种间接增强的算法，如小波反锐化掩模法。而基于参数优化的方法是通过选取某种参数因子对图像进行一定的调整，获得信息量突出的部分，从而实现图像增强。例如遗传算法图像增强法，其主要缺陷是参数的选择直接影响图像增强的效果。

小波变换提供了一种适合人眼视觉原理的多分辨率、显微镜性质的图像表示方法，经过数十年的发展，在理论和实践中取得了一系列令人瞩目的成就，成为图像处理领域中一个有力的工具[7-9]。随着研究的进一步深入，发现经典小波变换在处理二维图像时的主要不足是：变换提供的方向信息固定且有限，对自然图像中非水平或垂直方向的纹理信息表示能力不足。为了对图像的纹理信息实现更加有效的表示，研究者不断提出新的变换算法，如曲面波Curvelet变换[10]，Contourlet变换[11]等，但Curvelet变换的主要问题是对于高阶正则的奇异边缘不能达到最优的非线性逼近，增强后的图像边缘存在划痕；而Contourlet变换缺乏平移不变性，图像增强结果会产生Gibbs失真现象。美国学者Sweldens[12]于1997年提出提升小波，该方法使用提升框架来构造小波，算法简单、运算速度快，根据纹理方向相邻像素实现原点的预测和更新，能够更加有效地表示图像的纹理信息。Ding[13-14]在2007年提出方向提升小波变换，其主要贡献为在进行二维小波变换时不再局限于图像的水平和垂直方向，而是根据图像的纹理能够提供灵活的方向信息。尽管提升小波变换表示图像的纹理信息更丰富，但经典和提升小波共同的缺陷是：（1）小波基函数的长度限制所引起的高频部分的能量泄露，这种泄露使信号的能量-频率-时间分布很难定量给出，有时，小波的解释可能不是直观的，比如，如果要确定一个全局的变化，必须寻找在高频范围内的结果，因为频率越高，小波基就会越局部化，如果一个局部仅仅发生在低频范围，必须去寻找其对高频范围的影响，如果这是可能的，这种解释会很难。（2）和傅里叶变换一样，小波变换依赖基函数的选取，基函数决定了信号分析能力的强弱，因此对于具有较大差异的非平稳、非线性信号而言，小波在局部的分析能力较弱，只适合于全局分析。寻找更加有效的理论和工具，对图像的二维信息实现更加有效的表示，是众多研究者努力的方向，也是现在图像处理领域研究的一个热点问题。

EMD（Empirical Mode Decomposition，经验模式分解）方法[15]由Norden E.Huang等人提出，这种分解方法不再依赖于基函数，能够将复杂的信号分解成有限的几个固有模态函数分量（Intrinsic Mode Function，IMF）。由于分解是基于信号时域局部特征的，因此分解是自适应的，也是高效的，特别适合用来分析非平稳、非线性的时变过程，它能清晰地分辨出复杂信号的内蕴模式。

基于以上分析，本文提出一种新的增强算法，即基于EMD和自适应提升小波框架的图像增强，通过对二维图像信息作EMD分解，提取出图像信息的内模函数的IMF分量，然后对此IMF分量进行自适应提升小波分解并重构，得到增强图像。

1 EMD方法简介

1998年美国学者Norden E.Huang等提出了一种用来分析非平稳非线性数据的基于经验模式分解的算法，该算法突破了传统的傅里叶谱分析只能处理线性、平稳信号的缺点，它能够较好地分析非线性、非平稳信号。EMD是建立在如下假设基础之上的：（1）信号至少有两个极值——最大值和最小值。（2）时间特征尺度由连续极值的时间间隔决定。（3）如果数据没有极值而只有拐点，那么可以对其进行一阶或多阶的微分来获取极值，最终通过对分量的积分得到结果。EMD分解过程如下：将二维图像信号进行EMD分解，这种方法的精髓就是通过信号的时间特征尺度来确定固有振动模态，然后相应地分解这些数据。分解的方法可以使用各自的局部最大值和最小值形成的包络线。用三次样条曲线分别拟合所有的极大值和极小值点作为上、下包络线，然后对数据不断进行筛选，将其分解成n个IMF固有模态函数，IMF是满足两个条件的函数：（1）在整个数据集，极值和零点数目必须相等或相差最多不能超过一个。（2）在任何一点，由局部最大值极点形成的包络线和局部最小值极点形成的包络线的平均值为零。

在分解的过程中，首先对原始的数据信号取上、下包络线，获得的平均值并不是IMF，因为事实上，由于包络线样条逼近的过冲和俯冲作用，会产生新的极值，影响原来极值的位置和大小，因此，需要对包络线获得的平均值反复进行筛选，筛选过程主要有两个效果：消除畸形波和平滑波形，趋向末端时，筛选过程重复次数要多一些。对于第一个条件，对瞬时频率是必要条件；而第二个条件只在邻近波有太大的不等的振幅时才是必要条件。因此，数据筛选过程应谨慎使用。图1为对原始数据求得包络线后进行数据筛选的过程。

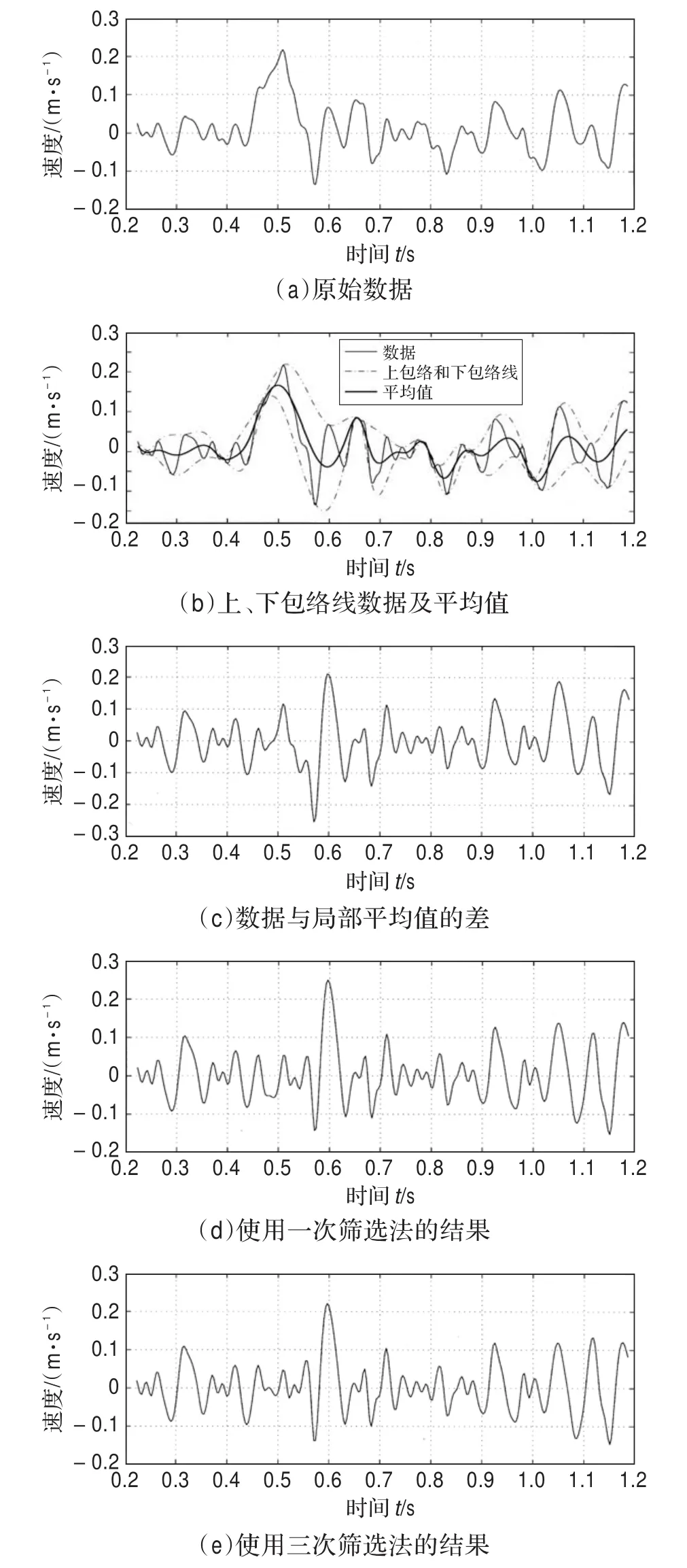
图1 数据筛选，获得IMF函数

2 方向提升小波变换算法

Ding于2007年提出方向提升小波，它与经典小波构造方法的主要区别是不依赖于傅里叶变换，在时间域中实现小波的构造。由方向提升方法构成的小波变换[13-14，16]过程主要分为四步：分解、预测、更新和重构。

（1）小波分解

将原始二维图像信号fi(x，y)分解成偶数子集合xe(m，n)和奇数子集合xo(m，n)。通用分解方法是将输入信号根据奇偶性分为两组。分解过程表示为：

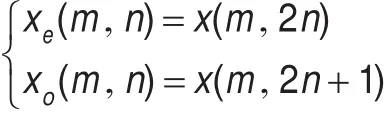
（2）小波预测

其中sign(x)是一符号函数，当x≥0时，其值为1，而x＜0时，其值为-1。

（3）小波更新

然后，由奇偶样本序列合并构成重构信号fi(x，y)。方向提升小波变换算法如图2所示。

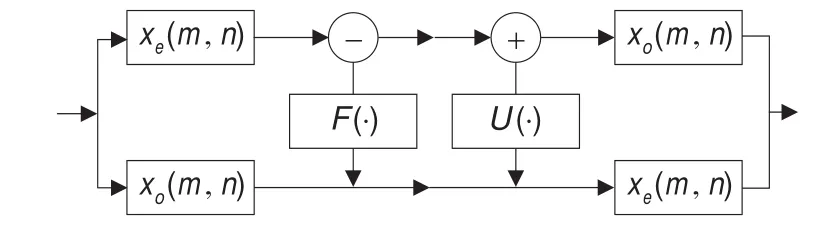
图2 方向提升小波变换算法

3 基于EMD和自适应提升小波变换的图像增强算法

尽管提升小波变换表示图像的纹理信息更丰富，但经典和提升小波具有两大共同的缺陷，一为小波基函数的长度限制会引起高频部分的能量泄露，二为小波变换依赖基函数的选取，基函数决定了信号分析能力的强弱，针对以上两大缺陷，首先对二维图像信息作EMD分解，提取出图像信息的内模函数的IMF分量，然后对此IMF分量进行自适应提升小波分解并重构，得到增强图像。

（1）已知二维图像信号为f(x，y)，对其进行EMD分解。

①用三次样条曲线分别拟合f(x，y)的所有极大值和极小值点，作为上、下包络线，上包络线与下包络线的平均值定义为m1，f(x，y)与m1之间的差为h1，即f(x，y)-m1=h1。

②筛选h1，第二次计算h1的上、下包络线的平均值定义为m11，h1与m11的差为h11，即h1-m11=h11。

③重复筛选过程k次，直到h1k为IMF分量，即h1(k-1)-m1k=h1k。

经过n次筛选后将h1k定义为IMF1，从f(x，y)中得到第一个IMF分量。

④将图像数据分解为n个IMF分量和剩余项rn，即

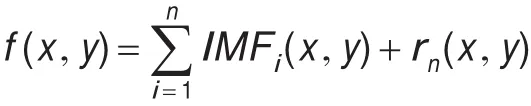
其中rn(x，y)为常数或为一个单调函数，不能再从中提取IMF分量，rn(x，y)可忽略。

（2）将信号IMFi(x，y)分解成两个较小的子集合ci-1(x，y)和di-1(x，y)，一般分解方法是将输入信号根据奇偶性分为两组，即

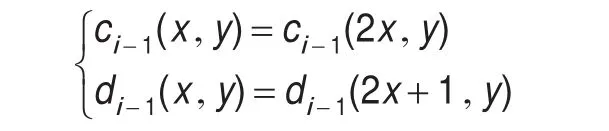
①在预测步骤中，用ci-1(x，y)来预测di-1(x，y)，其中预测误差为：

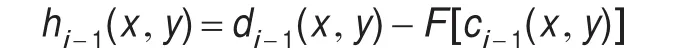
其中，F(·)为预测器，只要选定一种预测因子，就可以由ci-1(x，y)和hi-1(x，y)完全恢复di-1(x，y)信号。Ding提出的提升小波中，利用列方向的一组数据实现提升，本文在Ding提出的方向提升小波变换的基础上，采用自适应行方向来修正预测因子。

假定在di-1(x，y)点的行方向为ω，则预测因子就要修正为沿ω的行方向，即

其中sign(x)是一符号函数，即当x≥1时，值为1，而其他情况时值为-1。

如图3中，假定图像的像素与ω行方向具有很强的关联，在预测的过程中，“○”表示像素值的完整值，“+”表示像素的一半，“×”表示像素的1/4。当ω=0时，可描述为经典提升小波的特殊情况，相应的有限脉冲响应函数为：

图3 与ω行方向相关的自适应提升小波的预测和更新过程

在di-1(x，y)点的行方向为ω，则更新因子修正为沿ω的行方向，即

③给定hi-1(x，y)和li-1(x，y)的值，可以对小波进行完美重构。为了获得比较完美的重构信号，在子块图像像素点中对预测和更新过程作出描述。

在自适应提升的每个步骤中只需要利用相邻的有限个像素点值，通常选用最基本的Haar小波，Haar函数的定义为：

基于自适应提升小波变换的预测和更新过程如图3所示。

4 基于EMD和自适应提升小波变换的图像增强实验

利用3章提出的基于EMD和自适应提升小波的图像增强方法对大量图像进行实验，目的是为了验证本文方法的有效性。在实验室条件下，实验操作的平台是主频为Pentium IV 3 GHz，内存512 MB，操作系统WinXP的PC机，应用MATLAB和Visual C++对图像进行软件编程，小波滤波器选择Harr小波。测试图像选择标准图像库中的Lena.jpg（512×512）、Couple.jpg（512×512）、Pepper.jpg（512×512），并与经典小波变换算法[17]，提升小波变换算法，基于EMD的增强法[18]进行了比较，本文算法的整体增强效果优于上述对比算法。现选取有代表性的图像进行说明。三幅图像均具有背景偏暗且亮度不均匀的特点，从三幅图像增强结果的对比中可以看出：经典小波增强法由于只抓住了图像水平或垂直的纹理信息，对纹理信息表示能力不足，因此图像的增强效果不太理想。而提升小波变换算法由于在原位执行像素提升，因此表示纹理信息更丰富，增强效果要好于经典小波增强法。基于EMD的增强法存在的主要缺陷是在EMD进行分解的过程中由于图像区域点灰度值的剧烈变化和插值函数的过冲及欠冲，因此在增强图像的同时，放大了噪声。尽管提升小波变换表示图像的纹理信息更丰富，但经典和提升小波具有两大共同的缺陷，一为小波基函数的长度限制会引起高频部分的能量泄露，二为小波变换依赖基函数的选取，基函数决定了信号分析能力的强弱。针对以上两大缺陷，首先对二维图像信息作EMD分解，提取出图像信息的内模函数的IMF分量，然后对此IMF分量进行自适应提升小波分解并重构，得到增强图像，较好地改善了图像的整体增强效果。如图4至图6所示是上述几种图像增强的效果对比图。几种方法的图像增强量化对比数据如表1所示。

图4 第一组实验结果

图5 第二组实验结果

图6 第三组实验结果

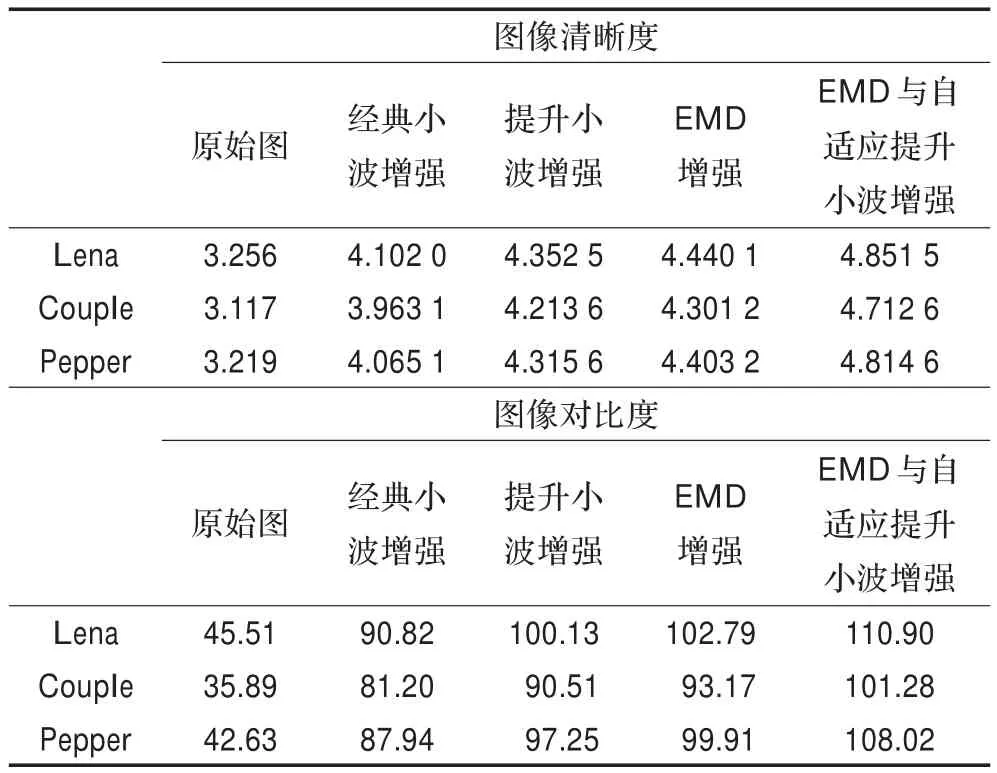
表1 所列方法的图像增强量化对比数据

图像清晰度表示对图像的特定细节信息的保留程度，清晰度越高，表示图像的局部特征越明显，所包含的细节信息越多。图像对比度指的是一幅图像中明暗区域最亮的白和最暗的黑之间不同亮度层级的测量，差异范围越大代表对比越大，差异范围越小代表对比越小，这是衡量图像增强结果好坏的重要指标。在Matlab中用函数std计算图像像素矩阵对比度。其具体格式为：x=std(r)，其中变量x是个数值，也就是结果大小，变量x的值越大说明图像的对比度越高，r是该图像对应的像素值矩阵。这一结果证明自适应提升小波增强对改善图像的质量是有效的。

5 结论

为了更好地提高图像增强的效果，本文提出一种基于EMD和自适应提升小波框架的图像增强方法。针对经典和提升小波方法共同的缺陷，首先对二维图像信息作EMD分解，提取出图像信息的内模函数的IMF分量，然后对此IMF分量进行自适应提升小波分解并重构，得到增强图像。实验结果表明，本文方法的综合性能优于经典小波变换法、提升小波变换法和基于EMD的增强法。本文方法可用于图像处理，目标跟踪等领域中的图像增强，对于亮度不均匀的含噪图像，增强效果尤为明显。

[1]Gonzalez R C，Woods R E.数字图像处理[M].阮秋琦，阮宇智，译.2版.北京：电子工业出版社，2007.

[2]Gonzalez R C，Woods R E.Digital image processing[M]. New Jersey：Prentice Hall，2002.

[3]Seow M J，Asari V K.Ratio rule and homomorphic lter for enhancement of digital colour image[J].Neurocomputing，2006，69（7/9）：954-958.

[4]Saitoh F.Image contrast enhancement using genetic algorithm[C]//Proceedings of IEEE Conference on Systems，Man and Cybernetics.Tokyo，Japan：IEEE，1999：899-904.

[5]Farzam F，Mcnhaj M B.Modified iterative fuzzy control based filter for image enhancement with multi-plicative noise removal property[C]//Proceedings of IEEE InternationalConferenceonImageProcessing.Paris，France：IEEE，1999：539-544.

[6]Cheng H D，Xu H J.A novel fuzzy logic approach to mammogram contrast enhancement[J].Information Sciences，2002，148（1/4）：167-184.

[7]张军，成礼智，杨海滨，等.基于纹理的自适应提升小波变换图像压缩[J].计算机学报，2010，1（1）：184-192.

[8]迟健男，张闯，张朝晖，等.基于反对称双正交小波重构的图像增强方法[J].自动化学报，2010，4（4）：475-487.

[9]李婵娟，梁德群，蒋妙龄.基于小波域的图像增强算法[J].哈尔滨工业大学学报，2009，11（11）：262-265.

[10]Candes E J，Donoho D L.Curvelets—a surprisingly effective nonadaptive representation for objects with edges[M]// Cohen A.Curve and Surface Fitting.Saint-Malo：Vanderbuilt University Press，1999.

[11]Do M N，Vetterli M.The contourlet transform：an efficient directional multiresolution image representation[J].IEEE Transactions on Image Processing，2005，14（12）：2091-2106.

[12]Sweldens W.The lifting scheme：a construction of second generation wavelet constructions[J].SIAM J Math Anal， 1997，29（2）：511-546.

[13]Ding W，Wu X，Li S，et al.Adaptive directional liftingbased wavelet transform for image coding[J].IEEE Trans on Image Process，2007，16（2）：416-427.

[14]Chang C L，Girod B.Direction-adaptive discrete wavelet transform for image compression[J].IEEE Trans on Image Process，2007，5：1289-1302.

[15]Huang N E，Shen Z.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proc R Soc Lond A，1998，454：903-995.

[16]Ding W，Wu F，Li S.Lifting-based wavelet transform with directionally spatial prediction[C]//Proceedings of the Process Picture Coding Symposium，San Francisco，CA，USA，2004：483-488.

[17]李云，刘学诚.基于小波变换的图像增强算法研究[J].计算机应用与软件，2008（8）：100-103.

[18]王星，安婧，沈小林.基于EMD的图像特征增强技术研究[J].山西电子技术，2009（4）：34-36.

LI Guangqiong,CHEN Rongyuan

College of Computer and Information Engineering,Hunan University of Commerce,Changsha 410205,China

An effective algorithm of image enhancement based on empirical mode decomposition and adaptive lifting wavelet analysis is presented.The image signal is decomposed to a number of IMF function via EMD;each IMF function is processed by adaptive lifting wavelet transform.The experiments of image enhancement show that this method is efficient and practical.

lifting wavelet transform;Empirical Mode Decomposition（EMD）;adaptive lifting wavelet transform;image enhancement

A

TP391

10.3778/j.issn.1002-8331.1212-0026

LI Guangqiong,CHEN Rongyuan.Image enhancement based on EMD and adaptive lifting wavelet transform. Computer Engineering and Applications,2014,50（21）：195-199.

国家自然科学基金（No.41101425）；湖南省科技计划项目（No.2012FJ4108）。

李广琼（1976—），女，讲师，主要研究方向为人工智能、图像处理。E-mail：liguangqiong0905@126.com

2012-12-03

2013-01-21

1002-8331（2014）21-0195-05

CNKI出版日期：2013-03-13，http://www.cnki.net/kcms/detail/11.2127.TP.20130313.0950.012.html