粒子群K-means聚类算法的改进

沈艳，余冬华，王昊雷

哈尔滨工程大学理学院，哈尔滨 150001

◎数据库、数据挖掘、机器学习◎

粒子群K-means聚类算法的改进

沈艳，余冬华，王昊雷

哈尔滨工程大学理学院，哈尔滨 150001

粒子群（PSO）与K-means结合是聚类分析中的重要方法之一，但都未考虑粒子更新导致的空类问题。提出基于多子群粒子群伪均值（PK-means）聚类算法，为该问题的解决提供一种有效途径，并与粒子群K均值（PSOK-means），K-means算法进行比较。理论分析和实验表明，该算法不但可以防止空类出现，而且同时还具有非常好的全局收敛性和局部寻优能力，并且在孤立点问题的处理上也具有很好的效果。

聚类分析；多子群粒子群；全局优化；K-means；PSOK-means

1 引言

K-means是聚类分析中广泛应用的算法之一，该方法对初始中心点的敏感，容易陷入局部极小解，聚类结果中类的个数及空类等问题一直都是研究的热点。与粒子群（PSO）结合的K-means聚类算法，在初始中心点，局部极小解方面收到了一定的效果，如刘靖明[1]，Kalyani[2]等。而在其基础上的改进算法，如混沌粒子群的CPSOKM方法[3]、变异粒子群K-means[4]、量子粒子群K-means[5]及KCPSO方法[6]在初始中心点及局部极小解问题上获得了极佳的效果，此外，针对聚类个数方面，有学者提出CPSOII动态聚类[7]及PM-K-means多类合并的粒子群K-means改进算法[8]。但是粒子群与K-means的结合或其改进算法，并没有解决聚类为空问题，与此同时，由于粒子需要在连续空间内更新，导致聚类中出现空类的几率大增，尤其是具备较高全局寻优能力的粒子，空类的出现，使得聚类结果远离预期目标类数，在类别划分中会淹没一些类的特征，并且淹没类的数据会被划分到其他所属类，弱化该类特征。在与粒子群结合或在其基础上改进的文献里，常见的做法是将其忽略，尽管这个问题不是经常出现，却是实际存在的。文中第4章给出实例，该例子说明只要粒子进入区域G，那么该类必定为空。

基于上述事实，本文综合K-mediods和并行粒子群思想，提出一种基于多子群伪K均值算法（Pseudo-K-means，简记为PK-means算法）。PK-means算法只需要调整“认知”和“社会”部分的学习因子就能调整粒子的全局寻优能力及局部寻优能力。伪均值的引入并不影响多子群粒子群的寻优、处理初始中心点及局部极小问题的能力，同时消除了聚类无解的情况。为描述上的方便，文中采用集合论中商集的相关概念给出PK-means算法的描述，便于文中在理论上说明聚类结果非空。对Iris和Wine数据实验表明，PK-means分类效果与PSOK-means一致，均比K-means准确、稳定，且没有空类现象。在增加孤立点后，适当增加聚类数目，可以将孤立点分成单独的类而不影响其他数据的分类。

2 多子群粒子群算法简介

多子群粒子群是在原始粒子群算法中，将粒子分为两个子群，对子群采用在局部和全局寻优能力上各有所长的不同更新策略。设Pi为第i个粒子曾经达到的最优解，为整个粒子群达到的最优解，那么r子群的粒子速度更新公式为：

其中，cr1，cr2，cr3，cr4分别为r子群和k子群的“认知”与“社会”部分的学习因子，r1和r2为[0，1]上的独立的随机数。ω为惯性权重：

在本文中，适应度函数就取聚类结果各个簇中数据对象到中心点欧式距离的平方和，记为：

针对于两个子群的划分，设粒子群有N个粒子，按照粒子适应度值从优到劣排序，子群划分比率为ρ，则r子群粒子为前[ρN]个粒子，其中[·]代表取整，剩下的就是k子群的粒子。由粒子的速度更新公式（1）与公式（2）可知，粒子更新主要涉及两个方面的影响，习惯上称为“认知”和“社会”部分。如果“认知”部分的影响超过“社会”部分，则更新后的粒子局部寻优能力强；如果“社会”部分影响超过“认知”部分，则更新后的粒子全局寻优能力强。因为r子群要倾向于局部搜索，所以“认知”学习因子要比“社会”学习因子大得多，而k子群要倾向于全局搜索，所以“社会”学习因子要比“认知”学习因子大得多。关于这方面更详细的理论阐述，可以参考文献[9]。这点正好为K-means聚类初始中心点问题提供了一种行之有效的解决方法。

3 PK-means算法的建立

3.1 PK-means商集描述

设X是样本数据集合，R是集合X的一个等价关系，集族X/R是集合X相对于等价关系R而言的商集，[x1]R，[x2]R，…，[xn]R代表商集X/R中的n个等价类。那么，PK-means划分为n个类的聚类就等价于存在n个中心点x1，x2，…，xn∈X，找到一个等价关系R*，使其满足如下条件：

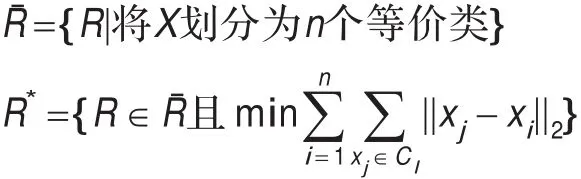
3.2 聚类非空性

根据商集的性质：（1）每一个等价类均非空；（2）不同等价类之间相交为空集，所有等价类的并集就是整个集合X。因为聚类结果中的每一个类就是商集中的一个元素，即一个等价类，由上述性质（1）可知，每一个类非空，且n个中心点x1，x2，…，xn∈X按照如下方式选取，每一次按照K-means方法计算第i类中心时，选取离该值距离最近的样本集点xi作为第i类的新的中心点进行聚类。这就对数据集进行了一个完美的划分，完成了聚类。最特殊的情况就是，该类只有中心点本身，仍然非空。

此外，由于中心点x1，x2，…，xn∈X，这就契合了K-medoids采用数据样本点作为聚类中心的聚类思想，顺承了K-medoids算法的优点，有效降低了孤立点对聚类结果的影响。

3.3 粒子编码

粒子群算法中的粒子，实质上是一个可行解，对应于划分成n个类的聚类问题来说，一个粒子就需要包含n个聚类中心点。设数据样本点有m个属性值，那么一个粒子就是一个n×m维向量，如果用Z代表一个粒子，那么该粒子可以编码如下：

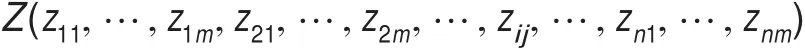
其中，zij代表第i个聚类中心点的第j维属性值。

3.4 PK-means算法描述

设数据样本集为X，参数集为Ω={X，N，n，ρ，cr1，cr2，ck1，ck2，ωmin，ωmax}pg，PK-means算法流程可以描述如下：

（1）读取数据，设定初始参数集Ω。

（2）初始化模型，设定粒子个数N，针对每个粒子分别在数据对象X中，随机抽取n个数据样本点作为初始中心点，根据公式（5）计算各个粒子的适应度值并排序。

（3）根据适应度值排序结果和子群划分比率ρ，对粒子群进行划分，得到r子群和k子群。

（4）r-子群和k子群分别按照公式（1）～（3）进行繁殖得到子代，用N个子代粒子作为N组均值初始中心。

（5）每一个粒子选择离均值初始中心最近的数据样本对象作为新的簇中心。

（6）将数据样本集中每个数据对象（再）指派到最相似的簇。

（7）计算每个簇的均值。

（8）对于每个簇的均值中心，选择离其最近的数据对象作为新的簇中心。

（9）判断中心点是否稳定，如果稳定，进行聚类，根据聚类结果得到新一组N个粒子的粒子群并计算其适应度值。然后转向（10），否则，转向（5）。

（10）比较适应度值。通过对比父代与其子代的适应度值大小，更新局部最优粒子pi，同时比较所有的父代与所有的子代适应度值。选取最大适应度值作为全局最优粒子pg。

（11）判断全局最优粒子pg是否满足结束条件，不满足转向（3），否则，结束程序，输出聚类结果。

4 实验仿真

4.1 聚类为空实例

在离散的样本点中，采用连续化方法选取中心点而不加处理，就可能导致某个中心点的聚类结果为空类。采用粒子群（PSO）方法优化的K-means方法就存在这个问题。下面将取Iris数据集中部分点（取72个样本，分别来自3个类别）作为例子说明聚类结果为空是可能的。

将该72个点划分为3类，此时粒子的可能解区域为矩形域[1.0，6.9]×[0.1，2.5]，某一次粒子更新后，有两个中心点分别为G1，G2，以G1，G2为圆心，以能够包含所有点的最小半径r1，r2作圆，然后再以G1，G2为圆心，以2r1，2r2作圆，划分出的区域如图1，而第三个中心点因粒子更新进入了区域G，聚类完成后，第三类将成为空类，因为任何一个数据点此时与第三个中心点的距离必定大于min{r1，r2}，故该数据点一定不会指派到第三类。

图1 部分Iris数据集聚类为空示意图

而伪均值算法将不会出现这种情况，如果采用K-means计算出均值落入区域G，所寻找的伪均值就是离该均值最近的一个样本点作为新的中心点，至少该点属于样本集，如假设初始化中心点或粒子更新后的聚类中心为x1，x2，x3，对应坐标值为（1.4，0.3），（3.0，2.0），（6.0，1.2），此时聚类中心x2所对应的类会成为空类，采用伪均值聚类后，会选择与聚类中心点最近的样本点充当伪均值，即图1中的x1'，x2'，x3'，对应坐标值为（1.4，0.3），（1.9，0.4），（6.0，1.8），而这三个聚类中心必定属于不同类别且均为样本数据点，故不会出现空类。

4.2 Iris与Wine数据集聚类仿真

为了从实验方面验证PK-means算法的聚类效果，下面对UCI（http：//archive.ics.uci.edu/ml/）上的Iris和Wine数据进行实验，该数据均可分为3类。其中Iris数据选取其第三与第四维属性值（petal length，petal width），Wine数据选取其全部的13个属性值，对于Iris数据点可以在平面用散点图反映，见图2。

图2 Iris数据散点图

使用PK-means对Iris数据和Wine数据聚类时参数设置如下：类数K=3，PK-means算法中的参数，N=10，ρ=0.5，cr1=0.2，cr2=1，ck1=0.5，ck2=0.5，ωmin=0.8，ωmax=1.2。在表1中，给出了聚类次数与Iris和Wine的各自的错分点个数，由于Wine的属性值比较多，故表中只给出了相应的Iris的初始中心点，PK-means算法的最优初始中心点分别为样本集中第49个，第98个，第129个数据点，其中，K-means聚类结果参照文献[10]。从表1可以看出，K-means对初始中心点的敏感程度非常大，虽然错分数可以接受，但是PSOK-means、PK-means无论是从对初始中心点的依赖程度，还是在分类的准确程度上，都能够好于K-means算法，有效减少了聚类的随机性，PK-means与PSOK-means具有相同的效果，并没有因为引入伪均值而降低聚类最终效果。

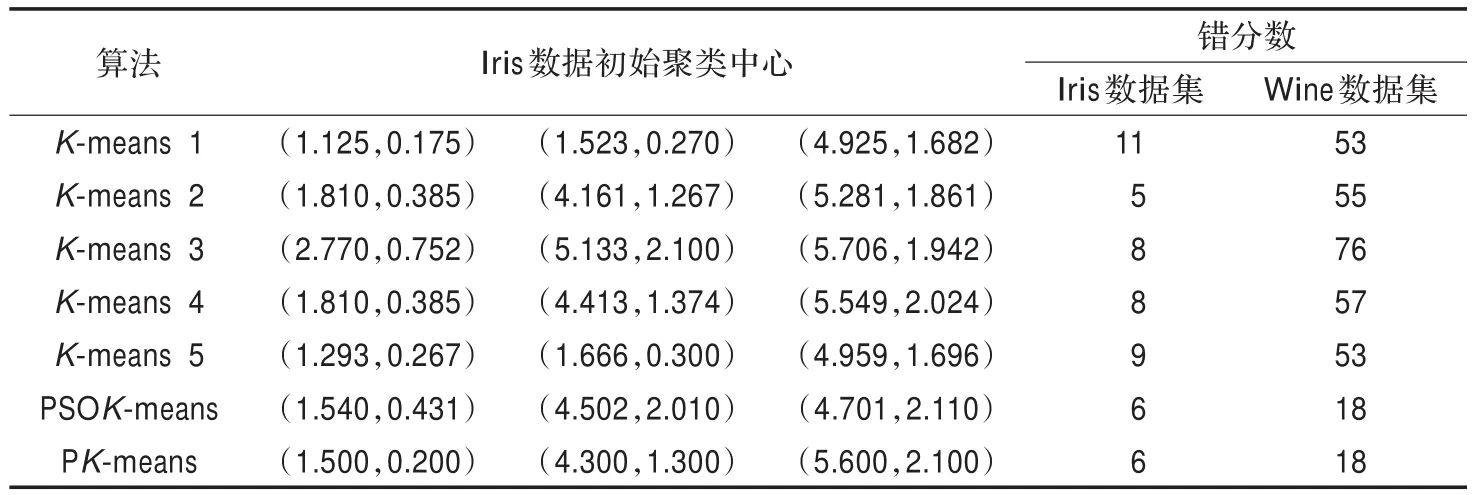
表1 分类结果

为了反映出多子群粒子群在算法中所起的作用，使用某次聚类过程中全局最优粒子更新代数和公式（5）的适应度函数值，画出初始中心点的调整（即粒子代数）与适应度函数值之间的曲线，如图3。Iris粒子适应度值每一次改变，都说明多子群粒子群找到了更优的初始中心点，即跳出了局部极小点，而Wine粒子的适应度值为直线，说明在初始化时，就已经找到了最优初始中心点。这也说明，加入的多子群粒子群算法起到了相应的效果。

图3 Iris与Wine粒子更新代数与适应度值关系

对于含有孤立点的数据来说，适当增加类数，即K值，一般可以把这些孤立点单独聚成类，而并不会影响数据分类，对于Iris数据，增加（14，0）与（20，0.2）两个点，这两个点很明显超出了原有数据的属性值范围而成为孤立点，对于Wine数据增加点（0，0，0，0，0，0，0，0，0，0，0，0，0），然后将增加了孤立点的数据聚成4类，结果如表2。

表2 加入孤立点后聚类结果

从表2可以看出，Iris数据集的第一个类只有两个数据点，恰为加入的孤立点（14，0）与（20，0.2），而Wine数据集的第三个类只有一个数据点，该点正是加入的那个孤立点，而对于其他的数据分类，错分数分别为6个与18个，并没有因为加入了孤立点而影响到分类效果。如果有必要，可以将分离开的孤立点剔除，然后再重新分类。

5 结论

PK-means算法综合了K-medoids算法和并行粒子群算法思想，在理论和实验上验证了该算法在克服初始中心点，局部极小，防止空类及处理孤立点问题上，都能收到很好的效果，并且在理论上论证了聚类结果非空的问题。此外，PK-means算法的收敛速度也很快，聚类的结果很稳定。值得指出，伪均值同样可以与混沌粒子群、变异粒子群及量子粒子群聚类算法结合，防止空类又不影响聚类准确性。

[1]刘靖明，韩丽川，侯立文.基于粒子群的K均值聚类算法[J].系统工程理论与实践，2005（6）：54-58.

[2]Kalyani S，Swarup K S.Particle swarm optimization based K-means clustering approach for security assessment in power systems[J].Expert Systems with Applications，2011，38：10839-10846.

[3]Li Y R，Zhu Y Y，Zhang C N.The K-means clustering algorithm based on chaos particle swarm[J].Journal of Theoretical and Applied Information Technology，2013，48（2）：762-767.

[4]王东，罗可.基于变异粒子群的聚类挖掘[J].计算机工程与应用，2011，47（21）：130-132.

[5]叶安新，金永贤.基于量子粒子群算法的聚类分析方法[J].计算机工程与应用，2012，48（32）：52-55.

[6]Cheng M Y，Huang K Y，Chen H M.K-means particle swarm optimization with embedded chaotic search for solving multidimensional problems[J].Applied Mathematics and Computation，2012，219：3091-3099.

[7]Masoud H，Jalili S，Hasheminejad S M H.Dynamic clustering using combinatorial swarm optimization[J].Applied Intelligence，2013，38：289-314.

[8]Lin Y C，Tong N，Shi M J，et al.K-means optimization clustering algorithm based on Particle Swarm Optimization and multiclass merging[J].Advances in Computer Science and Information Engineering，2012，168：569-578.

[9]闫允一.粒子群优化及其在图像处理中的应用研究[D].西安：西安电子科技大学，2008.

[10]连凤娜，吴锦林，唐琦.一种改进的K-means聚类算法[J].电脑与信息技术，2008，16（1）：38-40.

SHEN Yan,YU Donghua,WANG Haolei

College of Science,Harbin Engineering University,Harbin 150001,China

Combining particle swarm with K-means algorithm is one of the important methods in data mining,but all methods almost ignore the empty class problem which the particle update causes.This paper proposes a PK-means clustering algorithm based on multi-subswarms particle swarm and pseudo means,then is compared with both PSOK-means and K-means. The theory analysis and experiments show that the algorithm not only avoids empty clustering class but also has well global convergence and the local optimization,overcomes local minimum better,has a great effect on isolated data.

clustering analysis;multi-subswarms particle swarm;global optimization;K-means;PSOK-means

A

TP301

10.3778/j.issn.1002-8331.1401-0357

SHEN Yan,YU Donghua,WANG Haolei.Improvement of K-means based on particle swarm clustering algorithm. Computer Engineering and Applications,2014,50（21）：125-128.

国家自然科学基金（No.51309068）。

沈艳（1965—），女，博士，教授，研究领域为科学计算，系统建模，数据挖掘等；余冬华（1988—），男，硕士研究生，研究领域为科学计算，数据挖掘；王昊雷（1989—），男，硕士研究生，研究领域为数据挖掘，系统建模。E-mail：shenyan@hrbeu.edu.cn

2014-01-22

2014-03-27

1002-8331（2014）21-0125-04

CNKI出版日期：2014-05-29，http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1401-0357.html