混合快速细菌觅食算法求解非线性方程

郭德龙，郑添健，周永权

1.黔南民族师范学院数学系，贵州都匀 558000

2.广西民族大学信息与工程学院，南宁 530006

◎理论研究、研发设计◎

混合快速细菌觅食算法求解非线性方程

郭德龙1，郑添健1，周永权2

1.黔南民族师范学院数学系，贵州都匀 558000

2.广西民族大学信息与工程学院，南宁 530006

对于非线性方程组的求解，传统方法有很多，如牛顿法、梯度下降法等，但这些算法存在要求方程组连续可微、初值的选取是否合适等缺点，根据以上缺点将求解的问题转化为优化的问题，提出了新的交叉优化算法，充分利用细菌觅食算法局部搜索能力和粒子群算法的全局搜索能力，充分发挥了这两个算法各自优点。数值实验表明，新的算法可以弥补粒子群算法局部搜索能力弱和细菌觅食算法的全局搜索能力的不足，是求解非线性方程的有效方法。

局部优化；交叉；非线性方程

1 引言

经常遇到求解非线性方程组的问题在科学计算和实际工程领域。求方程的数值解是一个非常重要的研究内容之一，尤其是对于求解非线性方程的数值解。传统的算法有牛顿法、梯度下降法等[1-2]。但是这些算法的收敛速度以及解的精度是受初始值选取是否恰当影响的，同时如何去选择这个合适的初始点也是非常难。现代的智能优化算法如遗传算法、进化策略等虽在求解精度有了提高，但是也存在一个缺点那就是容易陷入局部最解。基于以上这些问题，研究和探索性能更好的算法是必要的。2002年，K M Passino基于大肠杆菌吞噬食物在人体肠道内一种行为，给出了一种新的群智能优化算法，细菌觅食算法[3]（Bacterial Foraging Algorithm，BFA）。并且此算法具有很强的全局搜索能力同时还具有群智能优化算法并行搜索能力。现在已成为计算智能领域研究的新的热点。模仿人体肠道内的大肠杆菌觅食是细菌觅食算法的主要行为，在搜索优化过程中搜索空间中的细菌的状态对应优化问题的解。

粒子群算法[4-5]是由Kennedy和Eberhart于1995年提出的一种基于群智能的随机优化算法。此算法模仿基点是群居的生物如鸟、鱼、蚂蚁等通过群聚来进行觅食和逃避被捕杀。在这类群体的动物整个群体中信息是共享的，而且每个个体的行为是建立在群体行为基础之上的，同时个体之间也存在着信息的交换与协作。在PSO算法中，粒子群在一个高维的空间中搜索是粒子通过个体和群体的飞行经历来不断调整自己的位置，同时每个粒子所处的位置都被看成解空间的一个。记做全局极值(xgbest)，第i个粒子所经历过的最好位置被记做个体极值(xpbest)。粒子根据下面的公式来更新自己的速度和位置：

其中r1，r2为[0，1]之间的随机数，c1，c2为非学习因子，w为非负惯性权重。

本文根据细菌觅食算法和粒子群算法的优点，给出了求解非线性方程的新算法。BFA模拟细菌群体行为，包括趋化、复制、驱散3个步骤。核心操作是趋化操作，一般包括翻转和前进两个过程，但由于BFA采取的是任意方向的翻转，收敛速度比较慢。而PSO中利用了个体极值和整体极值来更新位置的收敛速度快些。因此用PSO中的粒子移动的方式代替细菌的趋化操作步骤，即在细菌趋化中采用上面的公式（1），（2）进行细菌位置的更新。

2 问题的描述

设非线性方程：

的全部实根包含在(c，d)中，x*为方程（3）的任一固定实根，在[a，b]内只包含方程（3）的一个实根x*，[a，b]⊂[c，d]由优化理论易证方程（3）在[a，b]中的根x*等价于函数：

在[a，b]中的极小点，当H(x)最小值为0时，所对应的x即为方程（3）的精确解，H(x)最小值越小方程的近似程度越好。

3 细菌觅食算法描述

BFA算法包括趋化（chemotaxis）、复制（reproduction）和驱散（elimination-dispersal）3个步骤。

（1）趋化是指细菌聚集到营养丰富的区域。在这过程中运动方式包括前进和翻转。翻转是指细菌向任何方向移动单位步长。前进是指细菌完成一次翻转后它的适应度值得到改善，它将继续沿同一方向移动若干次直到适应度值不再改变，或达到预定的移动临界值。

（2）细菌进行繁殖。为简化计算法，可以规定复制繁殖的过程中细菌总数保持不变。以趋化过程中的每个细菌适应度值相加和为标准。较好的半数细菌分裂成两个子细菌，较差的半数细菌死亡。在这过程中遵循自然界“优胜劣汰，适者生存原则”。同时子细菌将继续继承生物特性，具有和母细胞相同的位置及步长。

（3）驱散过程指细菌在完成一定次数的复制后，将以一定概率被驱散到搜索空间中任意位置，也是加强算法全局寻优能力。对于复杂问题由复制和趋化无法避免陷入局部极小现象发生，但同时保留趋化过程可确保细菌局部搜索能力，复制过程能加快细菌的搜索速度。

4 混合算法求解非线性方程的设计

BFA算法中的核心是趋化操作为了更新细菌的位置，本文算法应用PSO中的粒子移动来更新细菌位置，而这充分利用了粒子群算法全局搜索能力强优点。充分发挥PSO算法全局搜索能力强，收敛速度快的优点，利用该算法的个体极值和全局极值来更新粒子位置。

混合算法的主要步骤如下：

步骤1给出细菌种群规模，迁移次数、复制次数、趋化次数和迁移概率进行参数设置。

步骤2首先设定每一个细菌的局部极值的初始值和全局极值的初始值，同时给出粒子群算法的参数。

步骤3随机生成初始化细菌群体。

步骤4计算细菌适应度值并进行评价。这里适应度函数取为：

步骤5执行细菌的三层循环操作

（1）内层循环（趋化性操作）按以下公式（8）进行细菌更新。包括更新个体最优和全局最优，并用公式（7）更新各细菌的速度。

其中w为非负惯性权重，c1，c2为非学习因子，r1，r2为[0，1]之间的随机数。

表1 本文算法与参考文献[5]对例1～例3的比较

表2 例4的数值结果

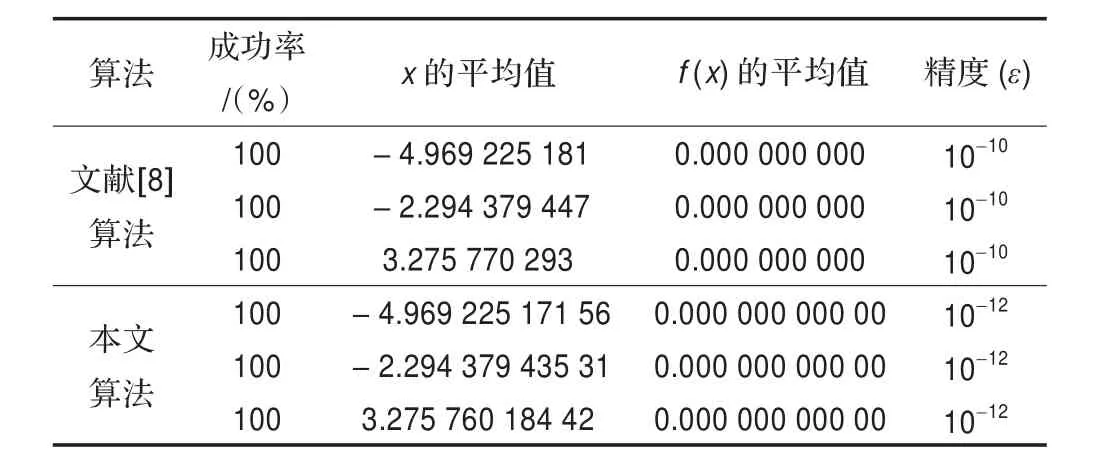
表3 本文算法与参考文献[8]对例5的比较结果

（2）复制操作：对于经过趋化性操作的细菌群体，并且对每个细菌的适应度值的累加和进行排序，淘汰掉适应度值较差的一半细菌再从剩下的一半细菌分裂出同样的细菌，遗传母细菌的位置和特性。

（3）迁移操作：通过上面的循环操作之后细菌可能走向局部极值。因此对于每一个细菌按照一定的迁移概率进行迁移，为了保证算法的收敛，设定一定的迁移细菌数目（凭经验值）。

步骤6输出群体最优解。

5 数值仿真实验

为了测试本文算法的性能，选取参考文献[5-8]的非线性方程。

数值实验在Matlab2010a中完成，为了保证该混合算法的可比性，各相关算法取相同的参数，细菌种群规模S=50，迁移次数Ned=2，复制次数Nre=10，趋化次数Nc=10和迁移概率p=0.25，采用惯性权重ω=0.7的线性递减策略，学习因子c1=c2=1.494，粒子数为50，r1，r2是[0，1]之间的随机数。

从表1～3比较结果可以看到本文所提出的混合算法收敛速度较快、求解的精度比较高，并且还能求出非线性方程的全部解。

6 结束语

本文提出了一种混合快速细菌觅食算法，充分将细菌觅食算法和粒子群算法（PSO）收敛性优点结合起来，应用在求解非线性方程数值解中。从数值计算结果可以看到本文设计该算法不仅有良好的稳定性而且有很高运算速度和精度，是一种可行而有效的优化算法，从而也为该算法在其他方面应用提供了一种新途径。

[1]李庆扬，莫孜中，祁力群.非线性方程组的数值方法[M].北京：科学技术出版社，1987.

[2]李庆扬，王能超，易大义.数值分析[M].北京：清华大学出版社，2008.

[3]Passino K M.Biomimicry of bacterial foraging for distributed optimization and control[J].IEEE Control Systems Magazine，2002，22（3）：52-67.

[4]Kennedy J，Eberhart R.Particle swarm optimization[C]// Proceedings of the 4th IEEE International Conference onNeural Networks.Piscataway：IEEEServiceCenter，1995：1942-1948.

[5]张建科.求解非线性方程及方程组的粒子群算法[J].计算机工程与应用，2006，42（7）：56-58.

[6]臧明磊，杨十俊.用遗传算法解一元非线性方程[J].济宁师专学报，1998，19（6）：1-2.

[7]高飞，奄恒庆.一类求解方程根的改进粒子群优化算法[J].武汉大学学报：理学版，2006，52（3）：296-300.

[8]张姣玲.求解非线性方程及方程组的人工蜂群算法[J].计算机工程与应用，2012，48（22）：45-47.

[9]王晓锋，张铁.一类求解非线性方程最优的8阶收敛迭代法[J].吉林大学学报：理学版，2013，51（4）：568-572.

[10]游煦.一类非线性方程近似解的改进Newton法[J].北京石油化工学院学报，2013，21（3）：62-66.

[11]倪健，马昌凤.解非线性方程的一种新的全局快速算法[J].合肥工业大学学报：自然科学版，2011，34（4）：620-622.

[12]张海蒂，曹德欣.求解非线性方程重根的区间牛顿法[J].计算机工程与应用，2012，48（31）：40-42.

[13]刘佳，周真真，夏少芳，等.基于人工蜂群算法的非线性方程组求解研究[J].自动化仪表，2013，34（2）：19-22.

[14]李超燕，赖红辉，周建良.基于极大熵和声搜索算法的非线性方程组求解[J].计算机工程，2011，37（20）：189-193.

[15]燕乐纬，陈树辉.基于改进遗传算法的非线性方程组求解[J].中山大学学报：理学版，2011，50（1）：620-622.

[16]王志刚.基于差异演化算法的非线性方程组求解[J].计算机工程与应用，2010，46（6）：54-55.

GUO Delong1,ZHENG Tianjian1,ZHOU Yongquan2

1.Department of Maths,Qiannan Normal University for Nationalities,Duyun,Guizhou 558000,China
2.College of Information and Engineering,Guangxi University for Nationalities,Nanning 530006,China

Traditional methods for solving nonlinear equations,such as Newton’s method,gradient descent method and so on,but they are required continuous differentiable,initial value selection.Aiming at above faults,the solution of the problem is transformed to an optimization problem.A new crossover foraging algorithm which is made full use of the ability of local search and particle swarm algorithm bacterial search ability,giving full play to the advantages of the two algorithms is proposed.Numerical experiments result shows that the new algorithm can make up for the lack of local search ability of particle swarm optimization algorithm and bacterial foraging algorithm global searching ability.This algorithm is an effective method for solving nonlinear equations.

local optimization;crossover;nonlinear equations

A

TP18

10.3778/j.issn.1002-8331.1401-0345

GUO Delong,ZHENG Tianjian,ZHOU Yongquan.Hybrid fast bacterial foraging algorithm for solving nolinear equation.Computer Engineering and Applications,2014,50（21）：32-34.

国家自然科学基金（No.61165015）；广西自然科学基金（No.0832082）；广西自然科学基金重点项目（No.2012GXNSFDA053028）；贵州省教育厅科研项目（黔教科2010093）。

郭德龙（1976—），男，副教授，主要研究方向为智能优化算法；郑添健（1976—），男，讲师，主要研究方向为计算机网络；周永权（1962—），男，博士，教授，主要研究方向为神经网络，计算智能及应用。E-mail：guodelong19760319@126.com

2014-01-21

2014-03-20

1002-8331（2014）21-0032-03

CNKI出版日期：2014-05-29，http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1401-0345.html