波动方程反演中边界条件下延拓的稳定性
李岩波,郭 华
(吉林大学数学学院,长春 130012)
波动方程反演中边界条件下延拓的稳定性
李岩波,郭 华
(吉林大学数学学院,长春 130012)
通过建立弹性波动方程反演中边界条件下延拓的过渡矩阵,得到了边界条件下延拓的求解方法及稳定性条件,解决了弹性波动方程参数反演时延拓深度点上边界条件无法测定的问题,从而提高了反演速度和精度.
弹性波方程反演;边界条件;下延拓;过渡矩阵;稳定性
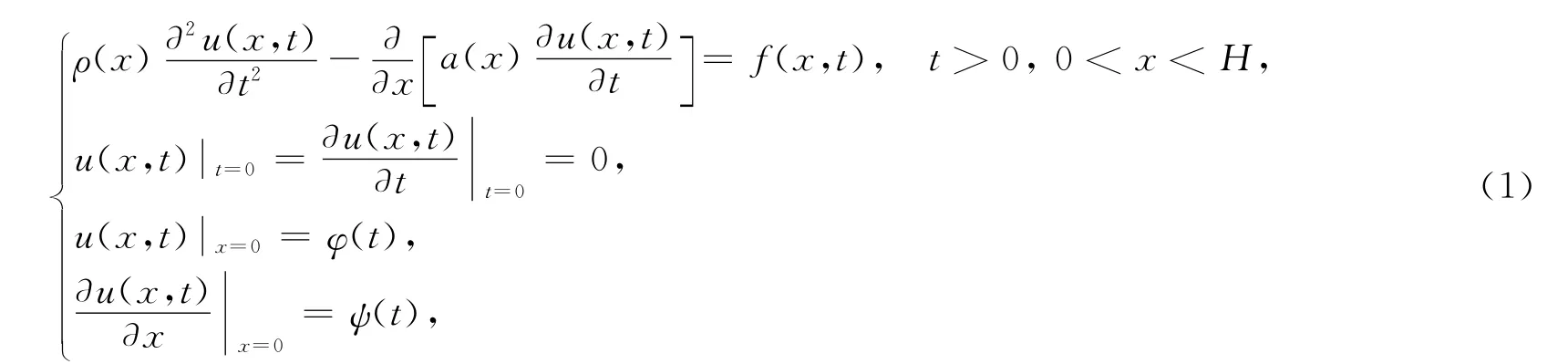
其中:变量x,t分别为深度和时间;u(x,t)为弹性介质内质点的位移;f(x,t)为已知函数;ρ(x)为地下介质的密度;a(x)=λ(x)+2μ(x),λ(x)和μ(x)为介质的Lame系数;φ(t)为地表边界条件;ψ(t)为震源子波,在地震勘探中常用δ-函数或Leike子波ψ(t)=e-αt2sin 2πft或ψ(t)=e-αt2cos 2πft模拟,常数α与振动的衰减有关,f是振动频率.
2 下延拓过渡矩阵
由于在频率域研究边界条件下的延拓问题较方便,因此将数学模型(1)做Fourier变换得
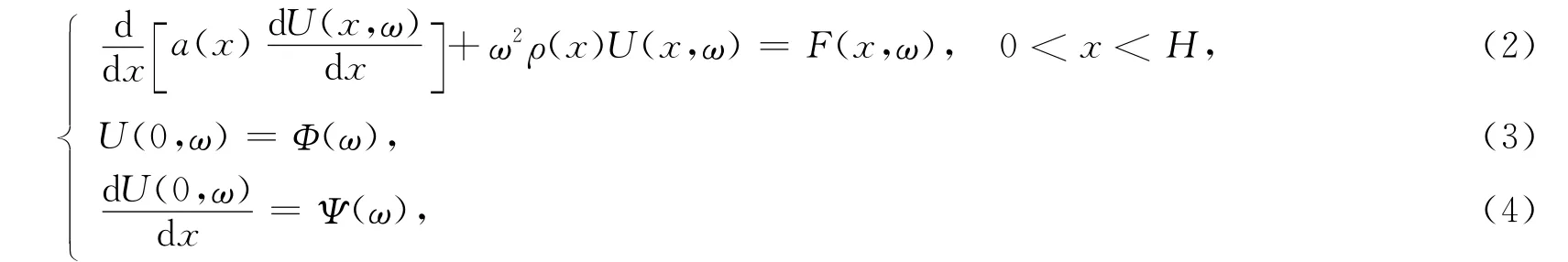
其中U(x,ω),F(x,ω),Φ(ω),Ψ(ω)分别是函数u(x,t),f(x,t),φ(t),ψ(t)的Fourier变换.将方程(2)和边界条件(3),(4)差分化得
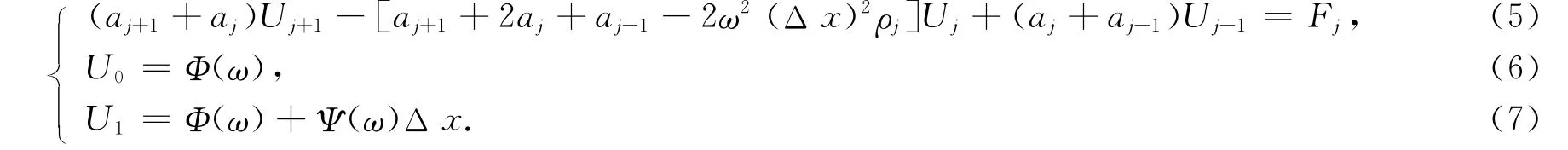

3 稳定性条件
边界条件下延拓的稳定性与下延拓过渡矩阵G有关.令
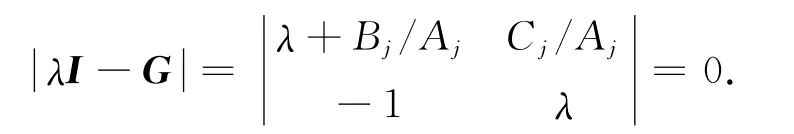
G的特征方程为Ajλ2+Bjλ+Cj=0.当根λ按模≤1,f(x,t)=0时,迭代格式(8)是稳定的[7],即边界条件下延拓稳定.

则稳定性条件仍然保持.式(9)和式(10)都是稳定性的充分条件,式(10)比式(9)稍弱,但应用较方便.
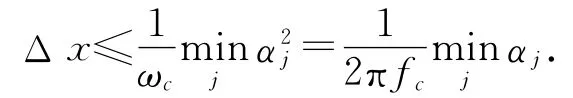

[1] GUO Hua,LIU Cai,LI Yue,et al.A New Inversion Method of Sedimentary Strata for Deriving Double Parameters and Its Applications[J].Journal of Geoscientific Research in Northeast Asia,2002,5(1):79-88.
[2] 何彦锋,孙伟家,符力耘.复杂介质地震波传播模拟中边界元法与有限差分法的比较研究 [J].地球物理学进展,2013,28(2):664-678.(HE Yanfeng,SUN Weijia,FU Liyun.Comparison of Boundary Element Method and Finite-Difference Method for Simulating Seismic Wave Propagation in Complex Media[J].Progress in Geophys,2013,28(2):664-678.)
[3] 任志明,刘洋.一阶弹性波方程数值模拟中的混合吸收边界条件[J].地球物理学报,2014,57(2):595-606.(REN Zhiming,LIU Yang.Numerical Modeling of the First-Order Elastic Equations with the Hybrid Absorbing Boundary Condition[J].Chinese J Geophys,2014,57(2):595-606.)
[4] Duchkov A A,Hoop M V,De.Velocity Continuation in the Downward Continuation Approach to Seismic Imaging[J].Geophysical Journal International,2009,176(3):909-924.
[5] Bai X Y,Liang K,Chen Y B,et al.Study and Application of Seismic Attenuation Based on the One-Way Wave Equation[J].Journal of Seismic Exploration,2011,20(1):45-55.
[6] 孙卫涛.弹性波动方程的有限差分数值方法[M].北京:清华大学出版社,2009.(SUN Weitao.The Finite Difference Numerical Method for Elastic Wave Equation[M].Beijing:Tsinghua University Press,2009.)
[7] 李荣华.偏微分方程数值解法[M].北京:高等教育出版社,2005.(LI Ronghua.Numerical Solution of Partial Differential Equation[M].Beijing:Higher Education Press,2005.)
(责任编辑:赵立芹)
Stability of Downward Continuation of Boundary Conditions of Wave Equation Inversion
LI Yanbo,GUO Hua
(College of Mathematics,Jilin University,Changchun130012,China)
The transition matrix of the downward continuation of boundary conditions about elastic wave equation inversion was established.The solving method and stable conditions of the downward continuation of boundary conditions were obtained.The problem that the boundary conditions at downward continuation depth points cannot be determined has been solved so as to improve the speed and precision of inversion calculation.
inversion of elastic wave equation;boundary condition;down continuation;transition matrix;stability
O175.2
A
1671-5489(2014)04-0743-03
弹性波方程的反演问题在地震勘探领域应用广泛[1-2],它能为储层描述提供所需的参数特征,是储层预测的确定性方法[3-5].若反演深度较大或分辨率较高,则反演的点数会显著增加,既增加了反演计算的不适定性,也延长了计算时间.若使用分段反演的方法,则不但在参数反演上是等效的,而且可以显著减少计算时间.弹性波方程参数的分段反演,需在每段上都有边界条件.但实际应用中只可能在第一段上获取地表边界条件的观测值,因而需要用理论计算求出其他各段所需的边界条件,即将地表边界条件延拓到各段上,作为各段的边界条件.本文给出了地表边界条件下延拓的方法和稳定性条件.
1 数学模型
若忽略横波效应,且假设仅深度与介质的变化有关,则地震波的传播满足下列弹性波方程的定解问题[6]:
10.13413/j.cnki.jdxblxb.2014.04.21
2013-12-31.
李岩波(1972—),女,汉族,博士,副教授,从事偏微分方程及应用数学的研究,E-mail:liyb@jlu.edu.cn.通信作者:郭 华(1964—),女,汉族,博士,教授,从事偏微分方程及应用数学的研究,E-mail:guohua@jlu.edu.cn.
吉林省自然科学基金(批准号:20130101179JC;201215165)、虚拟现实技术与系统国家重点实验室开放课题项目(批准号:BUAA-VR-13KF-14)和符号计算与知识工程教育部重点实验室开放课题项目(批准号:93K172013Z01).

