基于抽样近邻的协同过滤算法
董立岩,刘晋禹,蔡观洋,李永丽
(1.吉林大学计算机科学与技术学院,长春 130012;2.东北师范大学计算机科学与信息技术学院,长春 130117)
基于抽样近邻的协同过滤算法
董立岩1,刘晋禹1,蔡观洋1,李永丽2
(1.吉林大学计算机科学与技术学院,长春 130012;2.东北师范大学计算机科学与信息技术学院,长春 130117)
针对实时推荐过程中实际数据的稀疏性,满足条件的项目或用户较少,导致推荐精度较低的问题,提出一种采用抽样近邻的协同过滤算法.该算法充分利用评分用户矩阵提供的信息,增加了参与到预测评分计算过程中的用户或项目,从而解决了传统协同过滤算法在实际应用中的不足.实验结果表明,在增加在线计算时间较少的情况下所给算法可有效提高推荐精度.
协同过滤;稀疏矩阵;推荐精度;近邻
本文以近邻用户/项目组的选择作为切入点,充分利用现有评分矩阵提供的信息,以近邻组质量与推荐精度的关系为基础,提出一种抽样近邻的协同过滤算法(sampling neighbor collaborative filtering,SNCF).实验结果表明,该方法可有效提高推荐精度.
1 算 法
1.1 基于抽样的近邻查找策略
传统协同过滤算法在计算目标用户的预测评分时,一般直接从内存中读取过去某段时间计算过的其与所有其他用户间的两两相似性,由于数据量较大,且数据稀疏,一般仅筛选出最相似的K个用户作为近邻,导致曾经计算过的大部分相似性都不会参与到实际预测评分计算过程中,即很多计算是无用的,这种模式也导致了相似性的延迟性.而实时推荐中仅选择那些与目标用户有共同评分信息的用户计算相似性,有效减少了计算相似性的时间开销,但也会引入很多非正相关的用户到近邻用户组中.考虑到两种模式的不足,本文提出一种新的抽样近邻组查找策略.近邻查找策略步骤如下.
如果需要预测用户u对项目p的评分情况,主要参数有:近邻个数K和抽样因子α.
1)找到一个集合User,该集合是所有对项目p有评分的用户组成的集合;
3)分别计算出用户u与候选集User中每个用户元素间的相似性,将结果从大到小排序;
4)将3)中的结果取出前k个用户作为近邻用户组.
近邻中有部分用户可能并未对目标项目评过分,在计算预测评分过程中,本文选择用户评分均值取整[5]的方法作为对目标项目的评分.
1.2 基于抽样的近邻查找算法分析
初始数据中,由于用户集合项目集都较大,导致用户-项目评分矩阵过于稀疏,通过上述近邻选择方式选出的候选用户集则比原用户集小很多;新候选用户集的稀疏程度与抽样因子α成正比,由于实验中α的值过小,抽样后的用户集极大降低了稀疏度.此外,由于实际环境中对目标项目有评分信息的用户较少,新策略中本文将这些用户都添加到样本空间中,使这项历史行为信息能在预测评分过程中发挥一定作用;该方法还使一些没有对目标项目做出评分、但实际却和目标用户在一定程度上相似的用户参与到最终评分预测过程中的概率提高了.
如图1所示,左侧的“所有列”表示参与评分的所有用户,标记为集合U,其中对项目p有过评分记录的用红色记号标注,分别为U1,U2,U3,U4.计算“所有列”的稀疏率为1-4/14=71%.由于这些有评分信息的用户等概率的在用户集合中分布,本文假设用户集合按相似性降序以有评分信息的用户为界均分为(4+1)个桶,用户所在桶的编号越小,越与目标用户相似.按照上述策略,将{U1,U2,U3,U4}4个用户添加到“抽样列”集合中,设定抽样因子α=1,还需从a~j中再额外随机选择4个用户添加到“抽样列”中,因此“抽样列”集合的稀疏率为1-4/8=50%.“相关列”中所有用户都对目标项目评过分,因此稀疏率为0%.设近邻用户个数为4,假设集合都已按与目标用户的相似性降序排过序,则从抽样列选择未对目标项目评分但与目标用户很相似的用户和对目标项目有评分信息的用户各两个作为近邻用户,虽然相关列是对目标项目有评分信息的用户,但从所有列的排序中可见,有些用户的相关性与目标用户相差较远,如果他们加入到近邻用户组会影响近邻的质量.

图1 不同策略下的候选用户集Fig.1 Candidate set of users under different polices
由算法的时间复杂度可见,抽样近邻方法[6]比局部最优近邻法所需时间更多,这是因为选择用户数量增多的原因,选择用户数量增多则需花更多时间计算他们与目标用户间的相似性,但抽样近邻方法可提高推荐的精度,使用户获取正感兴趣的推荐.随着计算机科学的发展,可通过硬件资源的提高及算法的优化降低时间上的开销,使两种方法在时间复杂度上的差异越来越小,因此该方法以牺牲少量的计算时间为代价提高了推荐的准确性.
1.3 基于抽样近邻的用户协同过滤算法
由上述理论分析可知,新的近邻选择策略可对推荐结果产生有益影响,因此本文将这种近邻选择策略应用到传统基于用户协同过滤算法中,提出一种新的基于抽样近邻的用户协同过滤算法(sample neighbor user-based collaborative filtering,SN-UBCF).SN-UBCF算法除了应用近邻选择策略外,其他部分与UBCF算法相似,如用户间相似性计算、计算预测得分的方式等.主要步骤如下:
1)采用抽样近邻选择策略选出候选用户集;
2)计算出候选用户集中的用户与目标用户间的相似性;
3)相似性按降序排序,将前k个用户添加到近邻用户组,由于近邻用户中有未对目标项目评分的用户,因此将用户组分为对目标项目评过分的用户和未对目标项目评过分的用户两类;
4)采用近邻用户组中的相似性和评分信息计算目标用户对目标项目的预测评分.
上述算法的关键步骤是如何计算用户间的相似性,本文采用性能较好的Pearson相关相似性计算.文献[7-8]研究表明,通过增加相关重要性权重因子可降低共同评分信息少的用户间的相似性在计算评分中的权重,从而提高推荐精度,因此本文使用该相似性计算公式计算用户间的关系.用户u和v间的相似性为
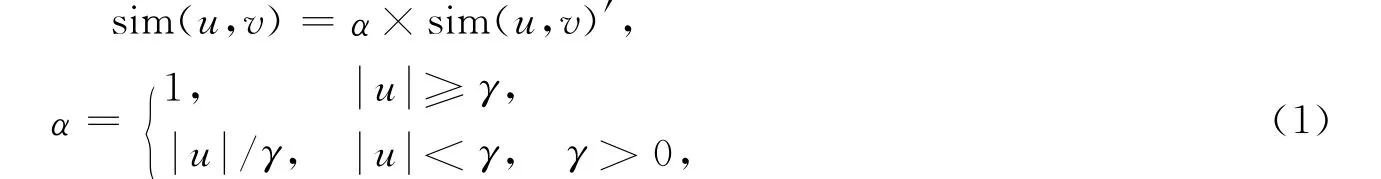
2 实 验
2.1 方 法
考察不同种类近邻选择策略应用到基于用户的协同过滤算法中对个性化推荐精度的影响.协同过滤算法要求用户设定某些参数,实验中测试多个参数对算法性能的影响.实验采用对折交叉验证方法[9],将MovieLens数据集5等分,依次选出其中的4份作为训练集,1份作为测试集.
2.2 评估指标
协同过滤算法多采用打分机制衡量用户对物品的兴趣度,因此推荐的过程相当于计算用户对物品的兴趣度分值,称为评分预测推荐.对此模式的质量评估,一般分析计算系统产生的预测分值与用户对项目的实际分值间差值的大小,差值越小则推荐结果越准确;反之则推荐结果准确性越差.实验中采用MAE作为度量标准[10]评价算法的性能:

其中:Rui表示用户u对项目i的评分;rui表示推荐系统的预测评分信息;T表示测试集合.
2.3 结果与分析
图2给出了传统协同过滤算法和SN-UBCF算法在不同近邻个数情况下推荐精度的变化情况.由图2可见,在不同近邻个数下,SN-UBCF算法都比UBCF算法的MAE值约低0.01,所以新算法可有效提高推荐精度.实验还度量了算法的计算时间,时间消耗在两部分:1)找到候选用户集所需的时间,即找出那些没有对目标项目评分的用户;2)计算出候选用户集中每个用户与目标用户间相似性所需时间.算法用时结果列于表1.由表1可见,SN-UBCF算法所需时间比UBCF算法高近1倍.算法采用Python实现,算法的执行效率较低,因此表1中的时间数据仅作说明使用,与实际应用环境中计算评测分值所用时间有较大差距.在实际工业环境中,可采用并行化算法实现核心部分,以减少算法的时间开销.由于计算相似性的用户集增大,所以在线时间一定会比原算法高,且该值与用户选择的抽样比例成正比,抽样用户越多,计算相似性需花费的时间越多;但由于选择的用户可能与目标用户没有共同评分项目,两者的相似性为0,不需计算,所以这种比例关系不是恒定的常量值,因此本算法在牺牲一定时间的开销下获得了较高的精度.
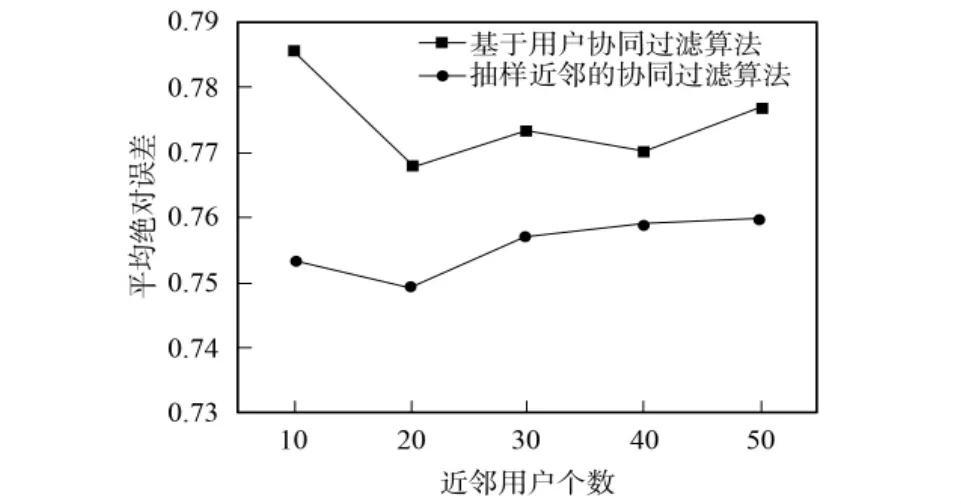
图2 不同k值时的精度对比Fig.2 Accuracies at different kvalues

表1 不同算法所用时间Table 1 Run time by different algorithms
综上,为使推荐结果更接近用户的实际需要,本文提出的基于抽样的近邻选择策略,不但理论上有合理性,且实际也符合用户的行为.还可将该方法应用在基于用户的协同过滤算法中,提出了SN-UBCF算法.实验结果表明,该算法在以增加少许的运算时间为代价的同时可极大提高算法的推荐精度.
[1] SONG Yang,ZHUANG Ziming,LI Huajing,et al.Real-Time Automatic Tag Recommendation[C]//Proceeding of the 31st Annual International ACM SIGIR Conference on Research and Development in Information Retrieval.New York:ACM,2008:515-522.
[2] Sarwar B M,Karypis G,Konstan J,et al.Item-Based Collaborative Filtering Recommendation Algorithm[C]//Proceedings of the 10th International Conference on World Wide Web.New York:ACM Press,2001:285-295.
[3] Sarwar B M,Karypis G,Konstan J,et al.Recommender Systems for Large-Scale E-Commerce:Scalable Neighborhood Formation Using Clustering[C]//Proceeding of the Fifth International Conference on Computer and Information Technology.New York:ACM Press,2002.
[4] Sarwar B M,Karypis G,Konstan J,et al.Application of Dimensionality Reduction in Recommender Systems:A Case Study[C]//Proceedings of ACM Web KDD Workshop.Minneapolis:University of Minnesota,2000:114-121.
[5] Xue G R,Lin C,Yang Q,et al.Scalable Collaborative Filtering Using Cluster-Based Smoothing[C]//Proceedings of the 28th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval.New York:ACM Press,2005:114-121.
[6] SHI Yue,Larson M,Hanjalic A.Exploiting User Similarity Based on Rated-Item Pools for Imprrved User-Based Collaborative Filtering[C]//RecSys’09:Proceedings of the Third ACM Conference on Recommender Systems.New York:ACM Press,2009:125-132.
[7] ZAHNG Jiyong,Pu P.A Recursive Prediction Algorithm for Collaborative Filtering Recommender Systems[C]//Proceedings of the 2007ACM Conference on Recommender Systems.New York:ACM Press,2007:57-64.
[8] Koren Y.Factor in the Neighbors:Scalable and Accurate Collaborative Filtering[J].ACM Transactions on Knowledge Discovery from Data,2010,4(1):1-24.
[9] Yehuda K.Collaborative Filtering with Temporal Dynamics[C]//Proceedings of the 15th ACM SIGKOD International Conference on Knowledge Discovery and Data Mining.New York:ACM,2009:447-456.
[10] Symeonidis P,Nanopoulos A,Papadopoulos A N,et al.Collaborative Filtering:Fallacies and Insights in Measuring Similarity[C/OL].2013-03-04.http://delab.csd.auth.gr/papers/WEBMINING06.pdf.
(责任编辑:韩 啸)
Collaborative Filtering Algorithm Based on Sampling Neighbor
DONG Liyan1,LIU Jinyu1,CAI Guanyang1,LI Yongli2
(1.College of Computer Science and Technology,Jilin University,Changchun130012,China;2.School of Computer Science and Technology,Northeast Normal University,Changchun130117,China)
Since the user-item matrix is sparse,and there are less users or items satisfying the conditions,the precision of the algorithm can’t be high.By sampling neighbor collaborative filtering algorithms,users take full advantage of score matrix provided information to increase the users or projects participated in the calculation process,so as to solve the shortage of traditional collaborative filtering algorithms in real application.Experiment results show that the new algorithm can effectively improve the precision in recommendation along a small increasing of runtime.
collaborative filtering;sparse matrix;precision of recommendation;neighbor
TP301.6
A
1671-5489(2014)04-0779-04
个性化推荐算法在Web服务中应用广泛,如电子商务、搜索引擎、多媒体服务中的个人影音和个性化阅读等,它可以提高服务的用户黏度.协同过滤算法在工业环境中应用广泛.针对特殊的推荐需求(实时推荐),如购物车推荐、新闻推荐等[1],需要根据用户当前的状态产生最新的推荐,但基于内存的协同过滤算法多数情况下需要预先计算用户或项目间的相似性存入内存中,使用时直接取值即可,导致产生的推荐具有一定的滞后性.
Sarwar等[2]为了减少在线运算的复杂性,在运算过程中仅选择了对最终项目有评分信息的用户,计算出这些用户与最终用户间的相似性,挑选出近邻用户组.但该方法可用的用户或项目较少,信息量较少导致推荐精度不高.文献[3]提出了基于模型的协同过滤算法,可有效减少在线计算时间,但也存在推荐滞后的问题.奇异值分解的矩阵分解算法[4]可降低用户项目评分矩阵的维度及计算相似性所用的时间,但推荐精度不高.
10.13413/j.cnki.jdxblxb.2014.04.28
2014-05-14.
董立岩(1966—),男,汉族,博士,教授,从事数据挖掘的研究,E-mail:dongly@jlu.edu.cn.通信作者:李永丽(1965—),女,汉族,博士,副教授,从事信息安全的研究,E-mail:Liyl603@nenu.edu.cn.
国家自然科学基金(批准号:61272209).

