基于连续时间T-S模糊模型非线性系统的稳定性分析
李 丽 芳
(吉林警察学院信息工程系,长春 130117)
基于连续时间T-S模糊模型非线性系统的稳定性分析
李 丽 芳
(吉林警察学院信息工程系,长春 130117)
针对一类连续时间非线性系统的稳定性分析问题,提出一种基于Takagi-Sugeno模糊模型的稳定性分析新方法.在模糊系统稳定性分析过程中,通过加入松弛矩阵技术,能充分考虑模糊隶属函数时间导数的有用信息,并显著增加稳定性分析的自由度,从而获得比已有稳定性判据保守性更小的连续时间Takagi-Sugeno模糊系统稳定性判据.所提出的稳定性判据以线性矩阵不等式形式给出,可方便地通过MATLAB数值软件求解.仿真实验验证了所提方法的有效性.
非线性系统;稳定性分析;T-S模糊模型;松弛矩阵
本文针对基于模糊Lyapunov函数的连续时间T-S模糊模型的稳定性分析问题,提出一种比已有研究结果保守性更小的稳定性分析方法.在设计过程中充分考虑了模糊隶属函数导数的有用信息,提出一种松弛矩阵技术,获得了比已有结果保守性更小的稳定性判据.仿真结果对比分析验证了本文提出方法的有效性.
1 模糊系统预备知识和引理
考虑由如下r条IF-THEN型模糊规则描述的连续时间T-S模糊系统[1]:

其中:x(t)∈Rn表示n维系统状态向量;ξ1(t),…,ξp(t)表示模糊模型的前件变量;Mij(i=1,2,…,p;j=1,2,…,r)表示模糊集;Ai∈Rn×n表示模糊模型的已知参数矩阵.
根据标准的T-S模糊推理方法,系统(1)的总体模糊模型可表示为

在已有采用模糊Lyapunov函数进行系统稳定性分析中,人们试图通过在设计中考虑模糊隶属函数随时间的导数信息减少所得稳定性判据的保守性,并常用如下关于模糊隶属函数导数的假设条件:
假设1 对于连续时间T-S模糊系统(2),假设其模糊隶属函数的导数变换界满足如下条件[14]:
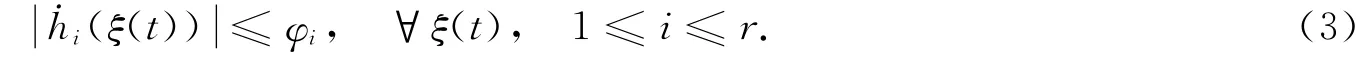
其中λi为模糊建模时确定的实数.
为方便,本文用x,hi和˙hi分别代替x(t),hi(ξ(t))和˙hi(ξ(t)).文献[10-15]证明了假设条件(3)在实际应用中的可行性,并给出了针对具体问题时φi的计算方法.文献[15]通过引入自由矩阵X,显著减少了连续时间T-S模糊系统稳定性判据的保守性.
定理1[15]考虑满足假设1的连续时间T-S模糊系统(3),若存在适当维数的矩阵M1和M2,对称矩阵M3和Pi(i=1,2,…,r),使得下列线性矩阵不等式成立:
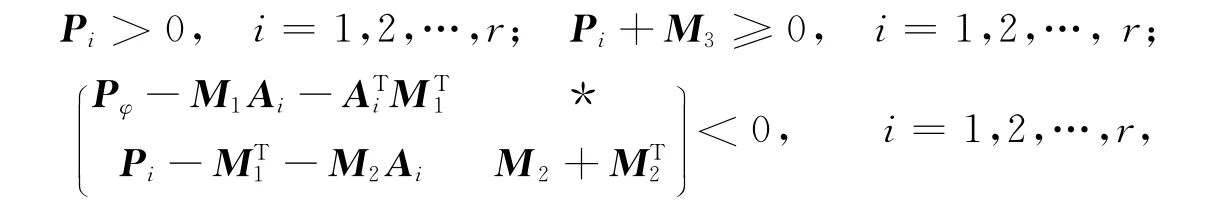
引理1 对于适当维数的对称矩阵X和R,如下两个命题成立:
1)对于-φi≤˙hi≤0,∀ξ(t),1≤i≤r,若有R<0和-φiX+R<0成立,则˙hiX+R<0成立;
2)对于-φi≤˙hi≤φi,∀ξ(t),1≤i≤r,若有φiX+R<0,R<0和-φiX+R<0成立,则˙hiX+R<0成立.
证明:1)对于对称矩阵X和非零向量x可知必有xTXx<0或者xTXx≥0.于是,在-φi≤˙hi≤0,∀ξ(t),1≤i≤r条件下,如果xTXx≥0,则有˙hixTXx≤0;否则有˙hixTXx≤-φixTXx.对于对称矩阵R,如果xTXx≥0,则有xT(˙hiX+R)x≤xT(R)x;否则有xT(˙hiX+R)x≤xT(-φiX+R)x,命题得证.
2)的证明与1)类似,故略.
2 主要结果
为进一步减少已有基于Lyapunov函数的连续时间T-S模糊系统稳定性判据的保守性,本文提出一种松弛矩阵技术,能更有效地考虑模糊隶属函数时间导数的有用信息,获得比文献[15]保守性更小的稳定性判据.
定理2 考虑满足假设1的连续时间T-S模糊系统(3),若存在适当维数的矩阵Mi1和Mi2,对称矩阵Xi和Pi(i=1,2,…,r),使得下列线性矩阵不等式成立:
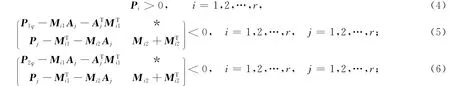
证明:对于连续时间T-S模糊系统(3)使用模糊Lyapunov函数

不等式(4)保证了上述Lyapunov函数的合理性.
对上述模糊Lyapunov函数沿系统(3)轨迹求取时间导数可得:
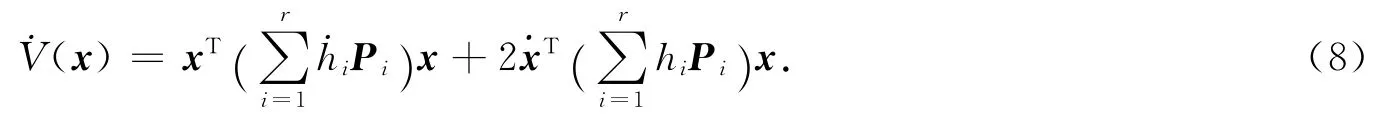
不失一般性,在任意时刻必有某个模糊隶属函数时间导数满足
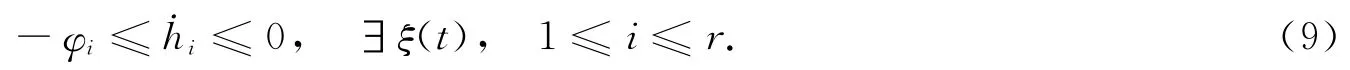
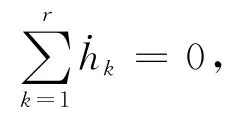
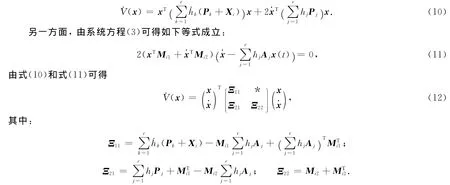
因此,由假设1、条件(9)和引理1可得到保证˙V(x)<0成立的充分条件为如下两个矩阵不等式成立:

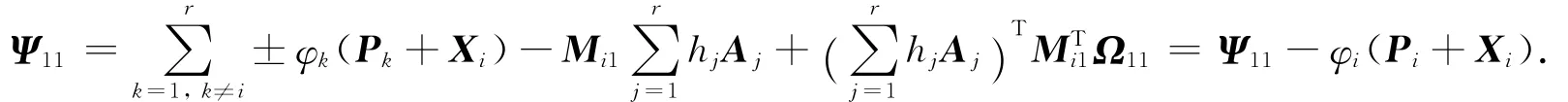
其中此时,若有线性矩阵不等式(5),(6)成立,则矩阵不等式(13),(14)也成立,即连续时间T-S模糊系统(3)是全局渐近稳定的.证毕.
注1 在定理2中,本文通过提出一种有效的松弛矩阵技术,引入了更多自由矩阵变量Mi1,Mi2和Xi,使所推导的稳定性判据在其设计过程中充分考虑了模糊隶属函数时间导数的有用信息,能显著减小结果的保守性.此外,与文献[15]相比,强约束条件Pi+M3≥0(i=1,2,…,r)在定理2中被合理去除,进一步增大了稳定性分析的解空间,减少了保守性.
3 仿真验证
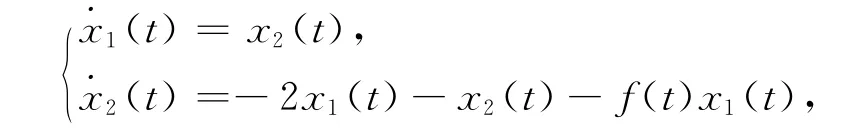
使用T-S建模方法建立上述非线性系统的模糊模型:
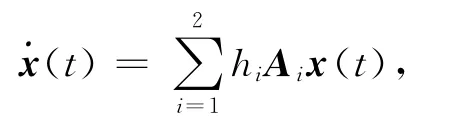
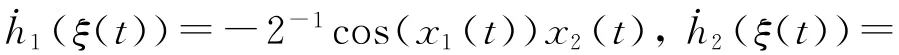
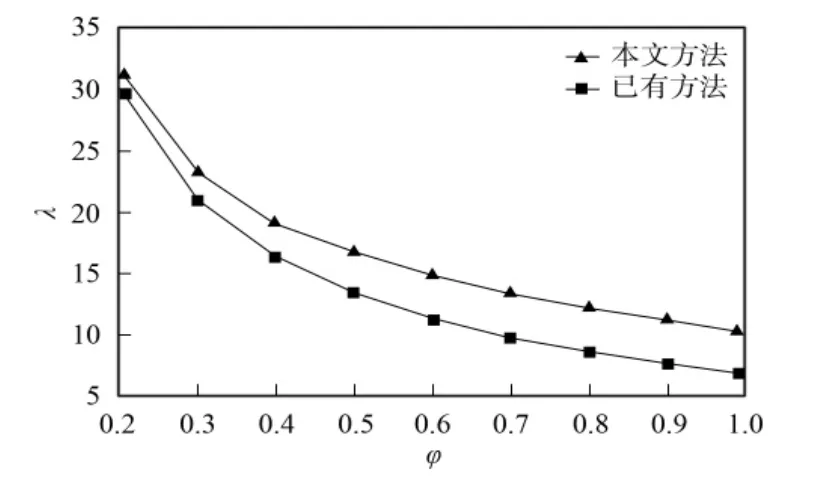
图1 不同方法得到系统参数λ的最大值比较Fig.1 Comparison between system parameterλ values obtained via different methods
本文使用MATLAB的LMItools计算在相同假设1条件下分别利用本文提出的定理2和文献[15]提出的定理1进行求解,并进行可变系统参数λ稳定范围的比较.本文将假设1中的参数设定为φi∈{0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0}(i=1,2).图1给出了在不同φi条件下分别使用文献[15]方法和本文方法得到的系统参数λ的最大值比较结果.由图1可见,对于每个φi,本文方法得到的λ最大值均大于文献[15]方法得到的对应值,即本文提出的连续时间T-S模糊系统稳定区域大于文献[15]得到的系统稳定区域,本文提出的稳定性判据具有更小的保守性.
下面在φi=0.5条件下选择λ=16.7,该点在文献[15]的T-S模糊系统稳定判据计算下是不稳定点,但本文的定理2能保证其为稳定点,即此时只有使用本文提出的定理2才能保证非线性系统在φi=0.5条件下当λ=16.7时是全局渐近稳定的.使用MATLAB LMI工具箱,求解线性矩阵不等式(4)~(6),可得到如下两个可行的Lyapunov矩阵:
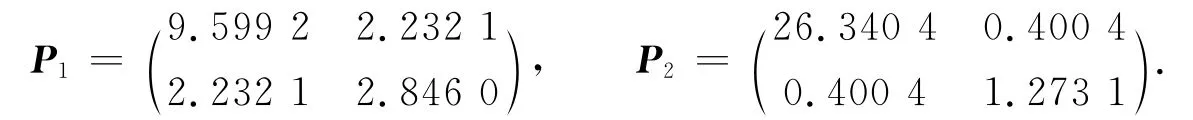
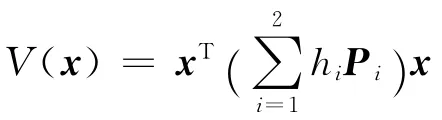
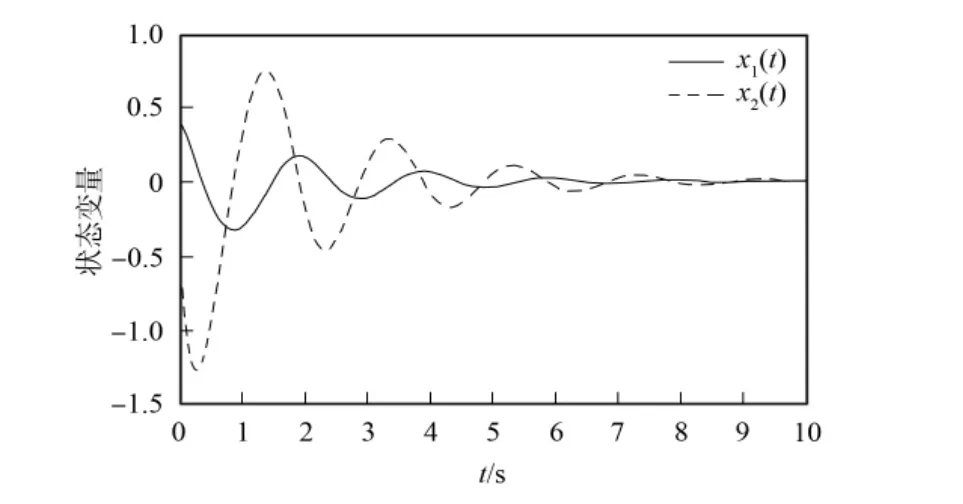
图2 系统状态向量轨迹Fig.2 Trajectory of system state variables
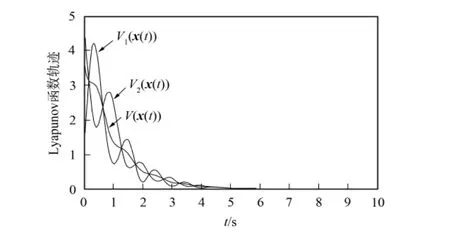
图3 V1(x(t)),V2(x(t))和V(x(t))随时间的变化轨迹Fig.3 Time trajectories of V1(x(t)),V2(x(t))and V(x(t))
综上所述,本文提出了一种连续时间T-S模糊系统稳定性分析问题的新判据.通过使用有效的松弛矩阵技术,充分考虑了模糊隶属函数时间导数的有用信息,可显著减少所得系统稳定性判据的保守性.仿真验证结果表明,本文方法与已有结果相比具有更好的优越性和有效性.
[1] Takagi T,Sugeno M.Fuzzy Identification of Systems and Its Application to Modeling and Control[J].IEEE Transactions on Syst Man Cybern,1985,15:116-132.
[2] WANG Lixin,Mendel J M.Fuzzy Basis Functions,Universal Approximation,and Orthogonal Least-Squares Learning[J].IEEE Transactions on Neural Networks,1992,3(5):807-814.
[3] Tanaka K,Ikeda T,Wang H O.Fuzzy Regulators and Fuzzy Observers:Relaxed Conditions and LMI-Based Designs[J].IEEE Transactions on Fuzzy Systems,1998,6(2):250-265.
[4] Kim E,Lee H.New Approaches to Relaxed Quadratic Stability Conditions of Fuzzy Systems[J].IEEE Transactions on Fuzzy Systems,2000,8(5):523-534.
[5] LIU Xiaodong,ZHANG Qingling.New Approaches to H∞Controller Designs Based on Fuzzy Observers for T-S Fuzzy Systems via LMI[J].Automatica,2003,39(9):1571-1582.
[6] Sala A,Ariño C.Asymptotically Necessary and Sufficient Conditions for Stability and Performance in Fuzzy Control[J].Fuzzy Sets and Syetms,2007,158(24):2671-2686.
[7] Sala A,Arino C.Relaxed Stability and Performance Conditions for T-S Fuzzy Systems with Knowledge on Membership Function Overlap[J].IEEE Transactions on Syst Man Cybern:Part B,2007,37(3):727-732.
[8] Montagner V F,Oliveira R,Peres P L D.Convergent LMI Relaxations for Quadratic Stabilizability and H∞Control of Takagi-Sugeno Fuzzy Systems[J].IEEE Transactions on Fuzzy Systems,2009,17(4):863-873.
[9] Tanaka K,Ohtake H,Wang H O.A Descriptor System Approach to Fuzzy Control System Design via Fuzzy Lyapunov Functions[J].IEEE Transactions on Fuzzy Systems,2007,15(3):333-341.
[10] Xie X P,Ma H J,Zhao Y,et al.Control Synthesis of Discrete-Time T-S Fuzzy Systems Based on a Novel Non-PDC Control Schems[J].IEEE Transactions on Fuzzy Systems,2013,21(1):147-157.
[11] Lam H K.Stability Analysis of T-S Fuzzy Control Systems Using Parameter-Dependent Lyapunov Functions[J].IET Control Theory and Applications,2009,3(6):750-762.
[12] ZHANG Huaguang,XIE Xiangpeng.Relaxed Stability Conditions for Continuous-Time T-S Fuzzy-Control System via augmented Multi-indexed Matrix Approach[J].IEEE Transactions on Fuzzy Systems,2011,19(3):478-492.
[13] Tognetti E S,Oliveira R,Peres P.Selective H2and H∞Stabilization of Takagi-Sugeno Fuzzy Systems[J].IEEE Transactions on Fuzzy Systems,2011,19(5):890-900.
[14] Mozeli L A,Palhares R M,Souza F O,et al.Reducing Conservativeness in Recent Stability Conditions of T-S Fuzzy Systems[J].Automatica,2009,45(6):1580-1583.
[15] Mozeli L A,Palhares R M,Avellar G.A Systematic Approach to Improve Multiple Lyapunov Function Stability and Stabilization Conditions for Fuzzy Systems[J].Information Sciences,2009,179(8):1149-1162.
(责任编辑:韩 啸)
Stability Analysis of Nonlinear Systems Based on Continuous-Time Takagi-Sugeno Fuzzy Model
LI Lifang
(Department of Information Engineering,Jilin Police College,Changchun130117,China)
A novel stability analyisis method was proposed for addressing the problem of stability analysis of continuous-time nonlinear systems based on the Takagi-Sugeno fuzzy model.In the process of stability analysis,a slack matrix method was applied to further considering the useful underlying fuzzy membership functions’time derivative.Owing to more freedom can be introduced in virtue of the slack matrix method,the obtained stability criteria are less conservative than those existing ones.Furthermore,the stability criteria proposed are given in terms of linear matrix inequality,which is easily solved via MATLAB numerical software.Finally,a numerical example was given to illustrate the effectiveness of the proposed result.
nonlinear systems;stability analysis;T-S fuzzy model;slack matrix
TP273
A
1671-5489(2014)04-0789-05
现实世界中的系统通常具有非线性物理特征,而系统稳定性分析问题是控制论研究的重点.Takagi-Sugeno(T-S)模糊模型[1]有效解决了一类非线性系统的数学建模问题.文献[2]证明了由于T-S模糊模型能以任意精度逼近定义在紧集上的一个连续非线性函数,在理论分析上赋予了基于T-S模糊模型非线性系统建模技术的合法性.在基于T-S模糊模型的非线性系统稳定性分析研究成果中,早期结果均选用单Lyapunov函数进行稳定性条件的设计,但由于这种单Lyapunov函数对于所有的模糊子系统使用同一个Lyapunov矩阵,因而所得到系统稳定性条件的保守性通常较大,在很大程度上限制了T-S模糊模型在非线性系统稳定性分析领域内的应用[3-8].为了减少所得稳定性条件的保守性,文献[4]提出了一种附件变量引入技术减少稳定性判据的保守性.文献[5-8]在文献[4]的基础上进行了改进,得到了保守性更小的稳定性判据.但由于单Lyapunov函数本身固有的缺点使上述结论很难从本质上对稳定性结果的保守性进行改善,要想进一步减少保守性就必须设计新型的Lyapunov函数.文献[9]提出了一种模糊Lyapunov函数,它能更充分考虑模糊隶属函数的有用信息,显著地减少了结果的保守性.在此基础上,人们提出了许多基于模糊Lyapunov函数的模糊系统稳定性分析结果[10-15].
10.13413/j.cnki.jdxblxb.2014.04.30
2014-02-28.
李丽芳(1970—),女,汉族,硕士研究生,副教授,从事控制论的研究,E-mail:lili_fang99@163.com.
国家自然科学基金(批准号:21127010).

