基于低碳理念的供应商订货量研究

刘 骏，任 龙

(1.东北财经大学金融学院，辽宁大连116023；2.清华大学经济管理学院，北京100084)

基于低碳理念的供应商订货量研究

刘 骏，任 龙

(1.东北财经大学金融学院，辽宁大连116023；2.清华大学经济管理学院，北京100084)

从绿色供应链的角度对核心企业供应商选择问题进行了建模求解，除考虑传统供需关系中的成本、质量、时间、敏捷性等主要因素外，将温室气体排放量纳入模型中。数值模拟说明：随着环境问题加剧，要想赢得更大市场份额，供应商不仅需要继续提高自身的响应速度，更需要降低温室气体排放量。随着低碳理念制度化，供应链上下级之间应以更加环保的方式实现双赢。

低碳；供应商选择；最优订货量

一、研究背景及文献综述

随着客户需求多样化与市场竞争加剧，企业管理者认识到横向一体化战略的局限性，转而寻求“纵向一体化”联盟。供应链管理(SCM) 突破了以往企业大而全的运作模式，把供应链中所有节点企业看作一个整体，涵盖整个物流和从供应商到最终用户的采购、制造、分销、零售等职能领域。

传统运作管理理念从TQCF等四个竞争要素方面对企业绩效进行衡量，SCM更是如此。其中主要包括时间、质量、成本以及快速响应能力。已有很多学者对此予以关注。[1][2][3]但实际上，企业往往无法从这四个方面全部领先于竞争对手，只能根据自身实际情况合理设计企业战略以满足市场需求。

随着全球气候变暖、环境问题日益突出，国际与国内相关组织对企业的可持续发展能力提出了新要求，顾客也对新的低碳绿色产品提出了新要求，这已为大势所趋。在竞争激烈的今天，如同马斯洛需求理论，客户对企业的要求也同样存在这样的需求层次。[4]当客户的低层级需求得到满足后必然转向更高层级需求。基于环保理念的绿色供应链管理正引起人们越来越多的关注。[5]低碳与绿色化程度也成为新竞争优势。

在此背景下，学者们提出了绿色供应链(Green Supply Chain)这一概念。这是一种以绿色制造理论和供应链管理技术为基础，在整个供应链管理过程中综合考虑环境影响和资源效率的现代管理模式。它涉及供应商、生产商、销售商、终端用户以及回收处理商，其目的是使整个产品生产过程对环境影响与负作用最小，实现最高的资源利用效率。[6]低碳供应链作为GSCM的拓展，在低碳排放方面提出了更多要求，但其本质上相同。

为适应多变的市场需求，企业越来越强调自身核心能力。供应商选择成为供应链管理决策中的一项重要内容。[7]供应商选择评价准则始于1996年Dickson的研究。[8]他认为，产品的质量、成本、交货期是选择供应商的最重要标准，这与TQCF标准不谋而合。能否选择合适的供应商，将直接关系到供应链整体成本及绿色化程度，进而增强供应链的整体竞争力。然而供应商选择涉及很多定性与定量因素，这是一个典型的多目标决策问题。[9]以往的评估方法包括线性加权模型、多目标规划模型、数学规划、数据包络分析(DEA)、[10]层次分析法[11]以及神经网络方法。[12]

在低碳供应链体系架构中，影响环境的有害物质多产生于供应链的上游。核心企业对于供应商的选择将在很大程度上影响整条供应链的绿色化程度，因此基于“低碳”供应链理念的供应商选择模型正变得越来越重要。

在供应商选择问题上，国内学者大都将目光集中于价格、供应时间及供应商能力等要素的评估，往往忽略了环保因素在供应商选择中的作用。[7]在低碳供应商评价上，王能民等学者提出了绿色制造模式下评价供应商的指标体系，在此基础上结合模糊决策的方法给出了评价模型。[13]很多即使使用了模型办法对问题求解的也都偏重供应商的选择而没有考虑订货量大小的问题。

本文从基本运作管理核心要素TQCF出发，考虑低碳要素在供应链协调与优化中的重要作用，从产品回收率、温室气体排放量、供应时间、供应商能力、成本要素等工程与非工程因素出发，通过核心企业利润最大化得出供应商选择的数学规划模型，并在第三部分结合我国电子行业实际企业给出数值结果。

二、模型建立

(一)基本假设

在本模型中，核心制造企业仅有一家，不考虑竞争关系。只考虑一种原材料的多供应商选择问题，且每单位原材料对应一单位制造商产成品。进货量没有整数限制。核心企业具备已存供应商的全部信息。

考虑到“低碳”理念，产品存在回收利用的问题，每个供应商供应材料的回收率为已知，为了满足国家或地方标准，产品必须达到一定回收率。

正常情况下，供应商的生产能力与生产时间成线性关系；当制造商对供应商提出更高数量要求时，超过部分的原材料的生产量与时间仍成线性关系，但比例系数发生变化。在本问题中没有考虑制造商由于未及时供货所带来的缺货损失，而用制造商在规定时间内提前交货的收益做替代。

产品利润包括一次售出利润、二次售出利润与提前供应奖励，其支出包括由于温室气体的排放而必须缴纳的税金。其中第一次售出利润为全新产品售出价格减去对应于相关供应商的转换费用，包括：运输成本、制造成本等要素；第二次售出利润为折旧产品售出价格减去第二次转换费用，其中包括：回收成本、维修费用等成本要素。

因环保需要，各地政府在制造过程中开始限制温室气体的排放量，假定每个供应商的单位原材料在生产过程中气体排放量为已知，国家的单位气体排放处罚也已知。

(二)符号说明

表1 符号说明

(三)累计生产时间设定

假定单一厂商在正常生产负荷情况下单位生产时间恒定。当生产负荷超过正常水平时，虽然所需时间与超过部分仍成线性关系，但此时单位时间提高。图1所示为生产量与累计生产时间的关系：单位生产时间随累计生产数量的升高而提高。

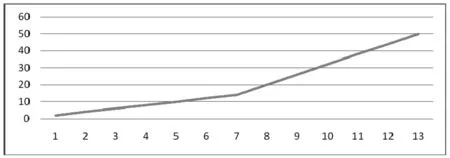
图1 生产量与累计生产时间关系

(四)供应商订货量决策模型

作为运筹学中的重要组成部分，数学规划在供应链决策、生产运作管理领域发挥了重要作用。[14][15]本文使用数学规划办法，目标函数为线性函数，而约束中存在非线性等式，总体上属于非线性规划(NLP)问题。

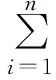
s.t.

xi1+xi2=xi

(xi1-Oi1)xi2=0

xi1≤Oi1

xi2≤Oi2

Ti≤t,i=1,2…n

Ti=xi1/ui1+xi2/ui2,i=1,2…n

xi≥0，xij≥0,i=1,2…n,j=1,2

上式为模型表达式，旨在求取核心企业利润最大值，其利润来自于三部分，即一次产品销售利润，二次产品销售利润以及提前生产奖励(由原材料的提前供应产生)，分别为上述模型中目标函数的第1、2、3项。在总的模型中，仅考虑由于温室气体排放而带来的罚款损失，为原目标函数的第4项。

约束部分：由于供应商生产能力有限，超额的生产将导致更长的单位生产时间，故核心企业对于每个供应商的需求应该被分成两部分考虑：正常生产能力下的需求及超常生产能力下的需求，这两部分的总和为核心企业对应于该供应商的总的原料需求量。接下来的约束为总的需求量不应超过核心企业的生产能力，核心企业对于各个供应商的需求量不应超过其总生产能力。

随着国家对制造业环保要求的提高，对制造企业的产品回收率与温室气体排放量做出了具体要求，接下来的两个约束描述了这方面的相关要求。从传统供应链的角度来看，也一定程度上反映了产品质量问题。

接下来的约束为非线性约束，模型描述了核心企业对于同一供应商的两种不同需求之间的相互关系，这也是结合下面的两种需求的非负性与最大生产条件所体现的。约束条件的意义在于，只有当正常条件下的供应商制造能力被达到后，才可以考虑增加其超长的生产能力。

最后关于时间的约束表示每个供应商的供货时间存在一个上界。为了处理简便起见，在本模型中假设正常与超常情况下生产时间与相对的生产数量之间成线性关系。随着研究的深入，也可以用更加精确并且复杂的模型对二者的关系进行处理。

三、电子行业企业应用

新的发展战略要求经济增长方式必须从粗放型经济转向绿色经济，绿色供应链的理念正得到人们越来越多的关注。就电子行业而言，其面临的挑战主要是如何有效地使用有限资源，在最大程度减少对环境危害的基础上创造最大价值。

(一)基本数据

根据本地区某电器企业的原始数据，在其基础上进行适当调整，得到各供应商的基本数据如表2所示：

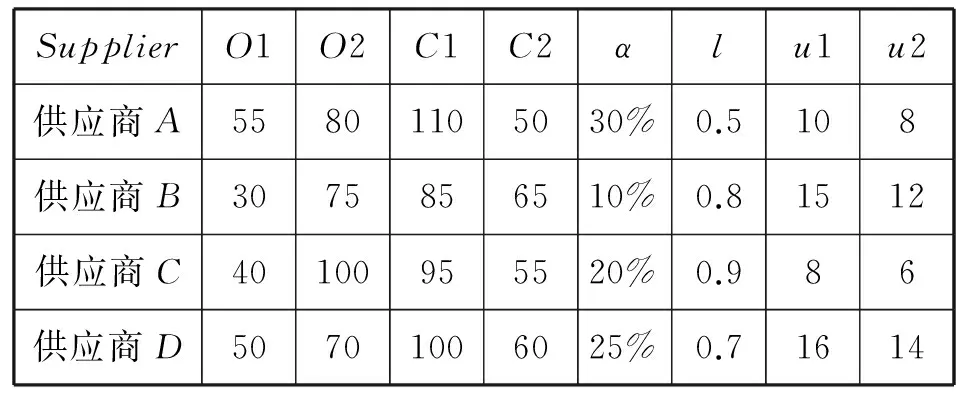
表2 供应商基础数据

核心企业的自身要求信息及相关常数如表3所示：

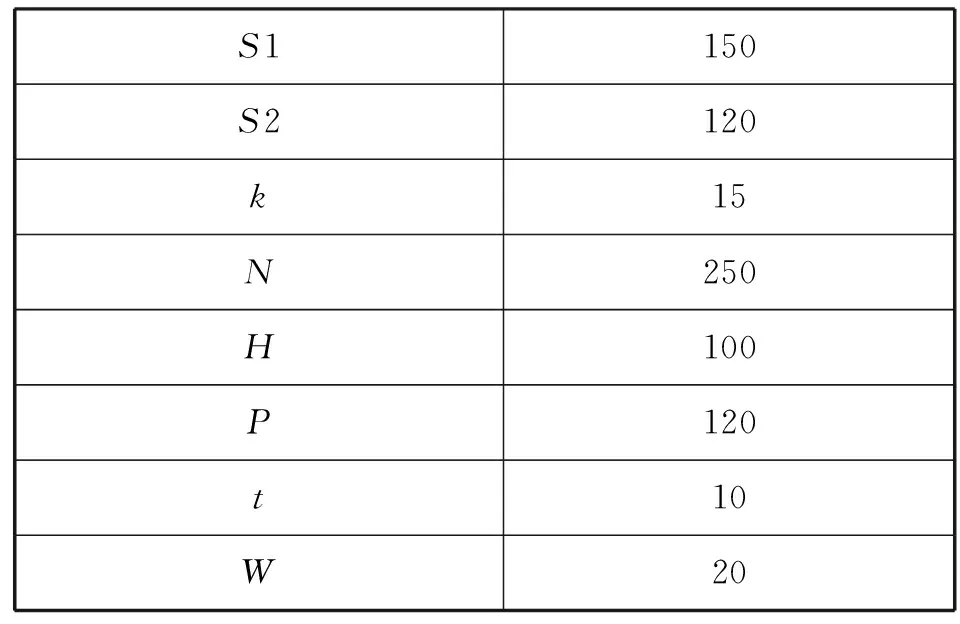
表3 问题常数

(二)最优订货量

使用Lingo软件进行求解。第一行表示在正常生产能力范围内核心企业对每个供应商的订货量。第二行是超过供应商生产能力的订货量。第三行表示总订货量。求解结果模型最优值为12573.9。

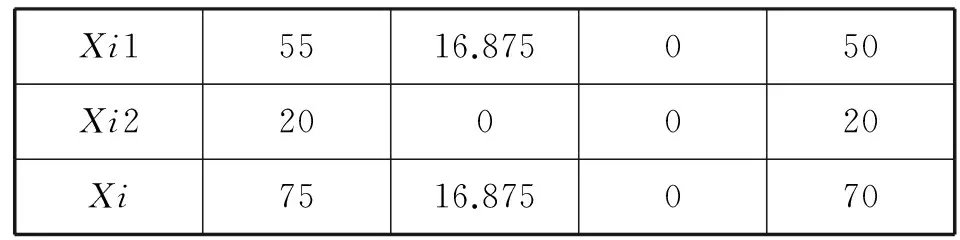
表4 最优解

四、结论与展望

本文从绿色供应链的角度对核心企业供应商选择问题进行了建模求解，除考虑传统供需关系中的成本、质量、时间、敏捷性等主要因素外，还将温室气体排放量纳入模型体系中。数值模拟表示：随着环境问题的加剧，要想赢得更大的市场份额，供应商不仅需要继续提高自己的响应速度，更需要降低温室气体排放量。随着低碳理念制度化，供应链上下级之间应以更加环保的方式实现双赢。这必将成为大势所趋。

本文仅考虑了诸如供应时间、产品回收率、温室气体排放量、核心企业成本等因素，在今后研究中应把更多因素纳入到这个体系中来。整条绿色供应链的优化问题也应该成为后续研究的重点。该模型中使用了非整数NLP建模办法，但在实际中，离散制造型企业的决策变量大多为整数型规划问题，这类问题的理论算法也是一个研究问题。另外，还有二者总利益最大化问题，这涉及供应商与制造商的利润分配与契约问题，需建立更科学的供应商选择模型予以分析。

[1] 文昌俊. 基于供应链管理的质量管理方法研究[J].湖北工学院学报，2004(3)：121-123.

[2]Martin Christopher, John Gattorna, “Supply chain cost management and value-based pricing”, Industrial Marketing Management, Volume 34, Issue 2, February 2005, Pages 115-121

[3]Xiao Tiao-jun, Jin Jiao, “Ordering, wholesale pricing and lead-time decisions in a three-stage supply chain under demand uncertainty”, Computers & Industrial Engineering, Volume 59, Issue 4, November 2010, Pages 840-852.

[4]C. A. Weber, J. R. Current, “A multiobjective approach to vendor selection,” European Journal of Operational Research, vol. 68, no. 2, pp. 173-184, July 1993.

[5]马士华，陈荣秋. 生产运营管理[M].北京：机械工业出版社，2010.

[6]谷立霞;，赵增朝. 电子产业绿色供应链管理研究[J]. 企业活力，2005(8)：62-63.

[7]董景峰，王刚，吕民，高国安. 基于改进蚁群算法的多供应商选择问题求解[J].计算机集成制造系统，2007(8)：1639-1644.

[8]Dickson G W. “An analysis of vendor selection systems and decisions”. Journal of Purchasing, 1996, 2( 1) : 521 .

[9]C. Y. Tam, V. M. Tummala, “An application of the AHP in vendor selection of a telecommunications system,” International Journal of Management Science, vol. 29, no.2, pp. 171-182, 2001.

[10]C. A. Weber, J. R. Current, and A. Desai, “Non-cooperative negotiation strategies for vendor selection,” European Journal of Operational Research, vol. 108, no. 1, pp. 208-223, July 1998.

[11]R. L. Nydick, R. P. Hill, “Using the Analytic Hierarchy Process to structure the supplier selection procedure,” International Journal of Purchasing and Materials Management, vol. 28, no. 2, pp. 31-36, 1992.

[12]V. Albino, A. C. Garavelli, “A neural network application to subcontractor rating in construction firms,” International Journal of Project Management, vol. 16, no. 1, pp. 9-14, 1998.

[13]王能民，孙林岩，汪应洛. 绿色制造模式下的供应商选择[J]. 系统工程，2001(2)：37-41.

[14]Brian Borchers, John Mitchell, “A computational comparison of branch and bound and outer approximation algorithms for 0-1 mixed integer nonlinear programs”, Computers & Operations Research, Volume 24, Issue 8, August 1997, Pages 699-701

[15]Lorenz T.Biegler, Gnacio E. Grossmann, “Retrospective on optimization”, Computers & Chemical Engineering, Volume 28, Issue 8, 15 July 2004, Pages 1169-1192.

(编辑：李学迎)

2014-05-06

F274

A

2095-7238(2014)07-0054-05

10.3969/J.ISSN.2095-7238.2014.07.012