基于PF-RBF神经网络的短期风电功率预测

王永翔， 陈国初， 张 鑫

(上海电机学院电气学院， 上海 200240)

基于PF-RBF神经网络的短期风电功率预测

王永翔， 陈国初， 张 鑫

(上海电机学院电气学院， 上海 200240)

为了提高风电功率的预测精度，研究了一种基于粒子滤波(PF)与径向基函数(RBF)神经网络相结合的风电功率预测方法。使用PF算法对历史风速数据进行滤波处理，将处理后的风速数据结合风向、温度的历史数据，归一化后构成风电功率预测模型的新的输入数据；利用处理后的新的输入数据和输出数据，建立PF-RBF神经网络预测模型，预测风电场的输出功率。仿真结果表明，使用该预测模型进行风电功率预测，预测精度有一定的提高，连续120h功率预测的平均绝对百分误差达到8.04%，均方根误差达到10.67%。

粒子滤波； 径向基函数； 神经网络； 功率预测； 风力发电

风能作为可再生能源的重要组成部分，是一种分布广、储量大、无污染的清洁能源，它的开发和利用已得到世界各国的高度重视[1-2]。

自然界的风往往具有很强的波动性、间歇性和随机性,其对风电场风电功率的输出具有较大的影响。当大规模风电并入电网时，风电功率的不稳定性将对电力系统的安全稳定运行以及电能质量都会产生很严重的影响[3]。因此，提高风速和风电功率的预测准确率对电力系统的稳定运行以及降低电力系统运行成本具有重大的实际意义。在风电功率预测的研究过程中涌现了许多方法，如时间序列法[4]、卡尔曼滤波法[5]、人工神经网络法[6]、支持向量机法[7]等，对风电功率都有较好的预测效果。然而，近些年也有不少学者提出了风电功率预测的组合方法，在一定程度上使预测精度有了很大提高。文献[8]中将改进的EMD(Empirical Mode Decomposition)算法与神经网络相结合，与单一的预测模型相比较，该方法在预测精度上有了很大提高。文献[9]中将信息融合技术应用到风电功率预测中,提出了一种基于交叉熵理论的风电功率组合预测方法，有效地提高了预测精度。

本文利用粒子滤波(Particle Filter， PF)算法对历史的风速数据进行平滑滤波处理，剔除风力发电机运行过程中的奇异点；然后，由处理后的风速结合历史风向、温度等数据得到风电功率预测模型的新的输入数据；最后，利用建立PF-RBF神经网络模型对风电功率进行预测。仿真结果表明，预测精度有一定的提高。

1 粒子滤波算法

PF的思想是基于贝叶斯估计原理利用粒子集来表示概率的蒙特卡洛(Monte Carlo)模拟方法，可以很好地用于非线性系统的处理[10-12]。历史风速数据可以看成是一系列波动性离散的点集，PF可以通过系统的状态空间模型，充分利用k-1时刻的状态值，并结合当前的观测值对k时刻的数据进行滤波处理。

1.1PF数学模型及实现步骤

PF建立在贝叶斯估计的基础上。贝叶斯估计主要通过先验知识和实际观测的数据来构造未知系统状态的后验概率密度函数。假设状态空间模型为

xk=f(xk-1,uk-1)

(1)

观测模型为

yk=h(xk,vk)

(2)

式中，f(·)和h(·)为已知的状态函数和观测函数;xk和yk为系统在k时刻的状态量和状态的观测值；uk和vk分别为零均值的系统噪声和观测噪声，它们相互独立并独立于过去和当前状态。

PF是用先验概率密度p(xk|y1∶k-1)结合不断到来的新的观测值来修正先验知识，从而得到所需的后验概率密度p(xk|y1∶k)。由贝叶斯估计原理可知，后验概率密度通常可通过预测和更新两步来得到。

(1) 预测

p(xk|y1∶k-1)=

(3)

(2) 更新

(4)

PF通过贝叶斯估计Monte Carlo方法从后验概率密度p(x0∶k|y1∶k)中抽取N个独立同分布的样本，用经验分布来逼近状态的概率密度函数，使

(5)

式中，δ(·)为狄拉克函数；i=1,2,…，N。

通常从被引入的一个容易实现采样的重要分布函数q(x0∶k|y1∶k)中抽样,即

q(x0∶k|y1∶k)=

q(xk|x0∶k-1,y1∶k)q(x0∶k-1|y1∶k-1)

(6)

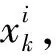
(7)

本文建立的PF算法风速数据处理步骤如下：

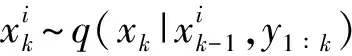
归一化权值,得

步骤3判断是否需要重新采样。计算有效粒子数为

若Neff≤NT,需要重新采样，则进入步骤4；否则，转入步骤5。其中，NT为样本阈值。

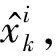
步骤5状态估计输出，

步骤6令k=k+1，返回步骤2。

1.2PF算法对风速数据的预处理

本刊讯：据《五粮液集团》报道，2018年11月23—24日，由中国百强论坛组委会、华顿经济研究院主办的“第十八届中国上市公司百强高峰论坛暨第四届中国百强城市全面发展论坛”在北京举行。四川五粮液股份公司以2017年度实现利润总额133.92亿元排名“2018年中国上市公司百强排行榜”第46位，获得“中国百强企业奖”。（江源荐，黄筱鹂编辑）

风速是风力发电机产生功率的主要因素。数值天气预报提供的历史风速数据的准确性往往直接决定着功率预测最终结果的可靠性。通过PF算法对历史风速的平滑处理可以更好地提高预测系统的预测精度。本文以东北某风电场6月份30天的风速数据为基础，每小时记录一组数据，共720组。设uk=1，vk=1，N=200，通过PF处理后的风速序列以及原始风速序列如图1所示。由图可见，两者基本吻合。

图1 原始风速和粒子滤波处理后的风速序列图Fig.1 Time series of wind speed and processed wind speed

2 PF-RBF神经网络预测模型

径向基函数(Radial Basis Function, RBF)神经网络是一种具有较强输入、完全映射能力的最优前向网络。与其他前向型网络相比，RBF网络具有结构简单、训练简洁、收敛速度快、局部逼近性能好及需设置参数少等优点，故被广泛应用于非线性优化、时间序列预测和模式识别等科学领域[13]。

2.1RBF神经网络结构

RBF神经网络具有3层前向网络结构，即输入层、隐含层和输出层[14]。该结构克服了BP神经网络中收敛速度慢及存在局部最小值的问题。其结构如图2所示。

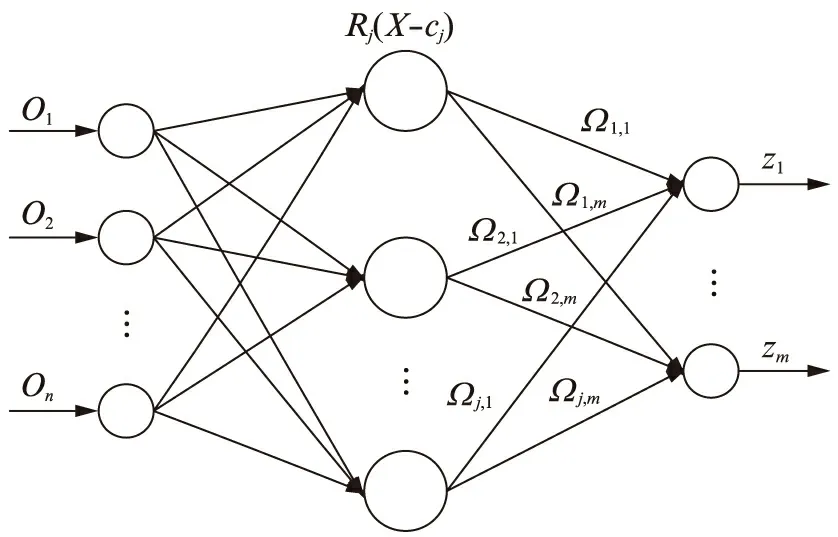
图2 RBF神经网络结构图Fig.2 Structure of RBF neural network

图中，O1,O2,…,On为输入层的实际输入值；n为输入层神经元个数，e=1,2,…,n；zξ为网络输出层第ξ个神经元的实际输出值；ξ=1,2,…,m,m为输出层神经元的个数；cj为第j个隐含节点基函数的中心；Ωj,ξ为隐含层第j个节点到输出层第ξ节点间的连接权值。

RBF神经网络的隐含层基函数通常选择高斯核函数，即

(8)

j=1,2,…，l

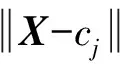
由图2可得到RBF神经网络的输入与输出之间的关系为

(9)

ξ=1,2,…,m

假设输入向量的期望输出值为s，Oe有Q个输入样本总数，那么上述方差可以表示为

(10)

RBF神经网络工作原理如下： 当输入值接近隐含层基函数中心范围时，隐含层的神经元就会感应出较大的输出，确定了RBF中心后，网络将输入值映射到隐含空间中，再根据隐含层神经元输出数据的加权求和(一般通过用线性函数映射)得到网络的输出值。

2.2PF-RBF神经网络风电功率预测模型

风电场采集到的风速呈现出随机波动震荡等特点，通过PF算法对历史风速进行平滑性处理，得到网络模型的新的风速输入数据，使数据的规律性得到进一步增强。然后，建立RBF神经网络模型，将新的风速数据结合历史风向和温度进行归一化处理，作为网络模型新的输入数据；最后，通过所建模型进行功率的预测输出。本文建立的模型PF-RBF神经网络风电功率预测流程如图3所示。

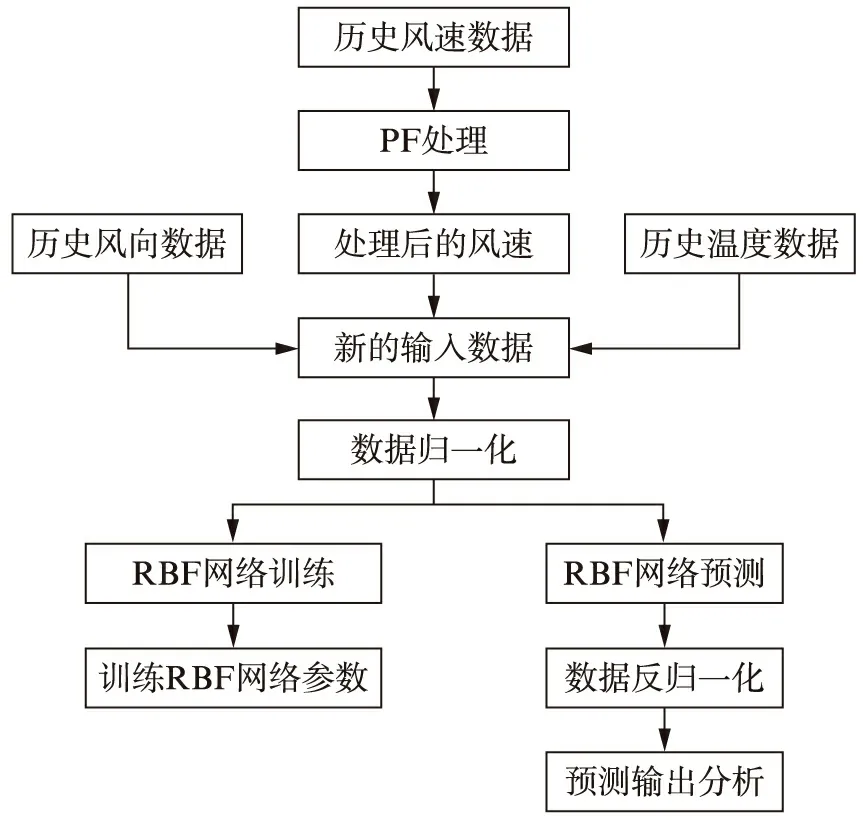
图3 PF-RBF神经网络风电功率预测模型Fig.3 Wind power prediction model based on PF-RBF neural network

PF-RBF神经网络风电功率预测步骤如下：

(1) 滤波处理。通过PF算法对历史风速数据进行平滑处理，由k-1时刻的风速结合新到来的观测值预测k时刻的风速状态，产生一系列规律性较强的风速数据。

(2) 数据归一化。将新得到的风速数据结合风向、温度等历史数据构成模型新的输入向量X，并进行归一化处理，即

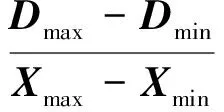
(11)

式中，D为归一化的输出；X为模型新输入数据，即风速、风向、温度共同构成的网络输入向量数据；Xmax、Xmin为新输入数据的最大、最小值；归一化处理后的输出最大、最小值分别设为Dmax=1，Dmin=-1。

(3) 训练网络。由RBF神经网络各层之间建立的映射关系，对网络进行学习训练确定网络的参数权值，建立网络预测模型。

(4) 网络预测。在训练好的网络模型中输入归一化后的风电功率测试数据，通过建立好的预测模型网络来获得功率的预测值。

(5) 反归一化。由于步骤(4)得到的是归一化后的功率，因此，根据式(12)将步骤(4)中得到的输出数据进行反归一化处理，计算出风电功率预测值为

(12)

(6) 预测分析。由输入的实际风电功率以及所建模型的预测输出功率在图表上显示出来，并计算其预测误差。

3 预测结果及分析

为了验证所建预测模型的有效性，本文以东北某风电场2007年6月份30天的数据为基础，每小时记录一组数据，共720组。利于PF算法对所有风速数据进行滤波处理，处理后的风速结果如图1所示。然后，剔除滤波过程中的奇异点以及风机非正常运行点，共剩余697组数据样本。在本文建立的PF-RBF神经网络风电功率预测模型中，选取前577组数据作为网络的训练数据，进行连续120h的风电功率预测实验，将预测结果与后120组数据进行比较，图4给出了利用Matlab实验平台仿真得预测结果与实际风速的比较。

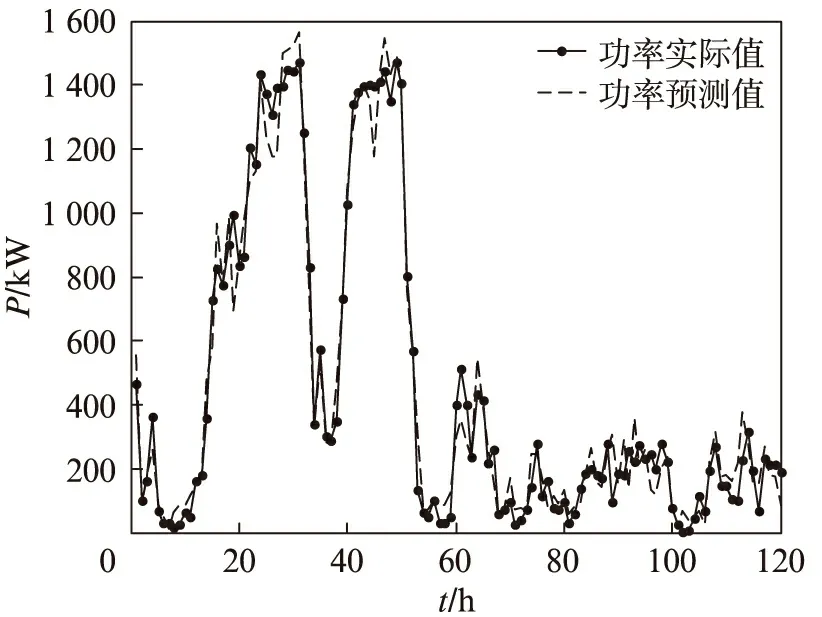
图4 连续120h功率预测值与实际值对比图Fig.4 Comparison of power prediction value and measured values in 120 hours

本文采用数据归一化后的平均绝对百分误差(Mean Absolute Percentage Error， MAPE)和归一化后的均方根误差(Root Mean Square Error，RMSE)对模型预测精度进行评价，其中，

(13)

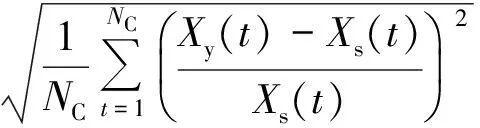
(14)

式中，Xs(t)为t时刻的实际值，Xy(t)为t时刻的功率预测值；NC为测试样本小时数。

通过Matlab实验平台仿真，并由式(13)、(14)计算得实验预测模型的MAPE=8.04%，RMSE=10.67%，误差结果在目前风电功率预测的允许误差范围内。此外，为进一步验证本文方法预测范围精度的准确性，通过多次仿真实验，分别计算连续48、72、96h的功率预测误差，表1给出了使用本文方法与单一的RBF神经网络预测模型[15]的MAPE比较结果。由表1可见，本文方法的预测精度有显著提高。

表1PF-RBF预测模型和单一RBF模型的MAPE比较结果
Tab.1 Comparison of MAPE of PF-RBF prediction
model and RBF model

4 结 语

本文提出的基于PF-RBF神经网络风电功率预测模型，通过PF算法对历史的风速数据进行平滑性滤波处理，以增强风速的规律性为预测模型提供更可靠的输入数据。然后，建立RBF神经网络预测模型，并将处理后的风速值结合其他的气象数据共同构成模型的输入。最后，通过归一化处理后的数据对网络参数进行训练，将新的测试数据输入网络实现预测功率的实时预测。仿真结果表明，本文给出的预测方法对短期风电功率预测具有很好的预测精度，在一定程度上对风电场功率预测以及电力系统的并网安全运行等提供了很好的实用信息。

[1] 刘永前，韩爽，胡永生．风电场出力短期预报研究综述[J]．现代电力，2007，24(5)： 6-11.

[2] 李晶，宋家骅，王伟胜.大型变速恒频风力发电机组建模与仿真[J].中国电机工程学报，2004，24(6)： 100-105.

[3] Ernst B, Oakleaf B, Ahlstrom M L, et al.Predicting the wind[J].IEEE Power & Energy Magazine,2007,5(6)： 78-89.

[4] Kamal L，Jafri Y Z.Time series models to simulate and forecast hourly averaged wind speed in Wuetta,Pakistan[J].Solar Energy,1997,61(1)： 23-32.

[5] Bossanyi E A.Short-term wind prediction using Kalman filters[J].Wind Engineering,1985,9(1)： 1-8.

[6] 范高锋，王伟胜，刘纯，等.基于人工神经网络的风电功率预测[J].中国电机工程学报，2008，28(34)： 118-123.

[7] 戚双斌，王维庆，张新燕.基于支持向量机的风速与风功率预测方法研究[J].华东电力，2009，37(9)： 1600-1603.

[8] 王鹏，陈国初，徐余法，等.改进的EMD及其在风电功率预测中的应用[J].控制工程.2011,18(4)： 588-591，599.

[9] 陈宁，沙倩，汤奕，等.基于交叉熵理论的风电功率组合预测方法[J].中国电机工程学报，2012，32(4)： 29-34.

[10] Gordon N J,Salmond D J,Smith A F M.Novel approach to nonlinear/non-Gaussian Bayesian state estimation[J].IEE Proceeding-F,1993,140(2)： 107-113.

[11] Kotecha J H, Djuric P M.Gaussian sum particle filtering[J].IEEE Transactions on Signal Processing,2003,51(10)： 2602-2612.

[12] 罗悦.基于粒子滤波的锂离子电池剩余寿命预测方法研究[D].哈尔滨： 哈尔滨工业大学，2012： 27-28.

[13] 何耀耀，许启发，杨善林，等.基于RBF神经网络分位数回归的电力负荷概率密度预测方法[J].中国电机工程学报，2013，33(1)： 93-98.

[14] 张德丰.MATLAB神经网络应用设计[M].北京： 机械工业出版社,2009： 157-159.

[15] 武小梅，白银明，文福拴.基于RBF 神经元网络的风电功率短期预测[J].电力系统保护与控制，2011，39(15)： 80-83.

Short-Term Wind Power Prediction Based on PF-RBF Neural Network

WANGYongxiang,CHENGuochu,ZHANGXin

(School of Electric Engineering, Shanghai Dianji University, Shanghai 200240, China)

To improve accuracy of wind power prediction, this paper proposes a short-term wind power prediction method combining a particle filter (PF) and a radial basis function (RBF) neural network. Historical wind speed data are first processed with a particle filter. The processed wind speed data combined with the historical data of wind direction and temperature are used as input to the model. A PF-RBF neural network of wind power output prediction model is established using the new input data. Simulation results show that the proposed model is accurate in wind power prediction. The mean absolute percentage prediction error in a period of 120 hours has been reduced to 8.04%, and the root mean square error is 10.67%.

particle filter(PF); radial basis function (RBF); neural network; power prediction; wind power generation

2014 - 06 - 10

上海市自然科学基金项目资助(11ZR1413900)；上海市教育委员会科研创新项目资助(13YZ140)；上海市教育委员会重点学科资助(J51901)

王永翔(1988-)，男，硕士生，主要研究方向为近海风电场风电功率预测，E-mail： 304611081@qq.com

指导教师： 陈国初(1971-)，男，博士，教授，主要研究方向为风电功率预测技术，E-mail： chengc@sdju.edu.cn

2095 - 0020(2014)06 -0324 - 05

TM 614；TP 183

A