分段线性减振系统的防跳跃及减振性能

雷娜，吴志强

（天津大学机械学院力学系，天津300072）

分段线性减振系统的防跳跃及减振性能

雷娜，吴志强

（天津大学机械学院力学系，天津300072）

为分析一类单自由度分段线性减振系统性能。先用平均法求得系统在主共振激励下的幅频响应方程，并基于约束分岔理论计算转迁集。再定性地分析转迁集各区域系统的幅频响应类型，得到避免跳跃的参数临界条件。数值计算验证了理论分析的可靠性。此外还讨论了阻尼比和激励幅值在非跳跃参数区域变化时，对系统力传递率及系统幅频响应峰值点力传递率的影响。研究结果证明较小激励情况下，阻尼比越大，减振系统的抗振动性能越好。

振动与波；分段线性；转迁集；跳跃；分岔；减振

分段线性减振系统是一类特殊的非线性系统，普遍存在于工程实际中[1]，如重载列车转向架悬挂系统，柴油机轴系安装的分段线性缓冲器，振动筛和振动输送机等采用的分组弹簧。采用此类非线性系统可在不改变减振系统固有频率的前提下，避免干扰频率与固有频率吻合，从而迅速降低响应峰值，极大的改善了系统的振动特性。

跳跃和滞后现象是非线性系统受迫振动的重要特征。非线性受迫振动系统减振设计的重要环节，就是预防有潜在危险的跳跃现象。因为跳跃现象可能引起某些设备或器件振动突然变得剧烈而遭到破坏，或者振动突然减弱而不能正常运转，所以对于分段线性减振系统，研究如何利用非线性特点且避免跳跃具有重要工程实际意义。

文[2]分析了分段线性系统的非光滑向量场对庞加莱映射的影响以及由此产生的复杂动力学行为；文[3]使用多项式拟合的方法将一类典型的分段线性系统的弹性力表示为级数形式，进而利用多尺度法对改造后的非线性方程求解，得到分段线性保守自治系统解析解的通用公式；文[4]研究了减振器中弹性限位器的设计，指出传统设计在小阻尼情况下非常危险，会出现意想不到的主共振、亚谐共振和混沌响应；文[5]应用奇异性理论分析了分段线性非线性汽车悬架系统的分岔行为，由系统参数与系统的分岔解间的关系，得到不同参数下系统的运动特性；文[6]研究了阻尼以及2阶初始位置等参数对分段线性减振系统的振动性能和抗冲击性能的影响；文[7-9]以非线性发动机悬架模型为研究对象，根据只要频响曲线出现两个垂直斜坡（即临界振幅），就会发生跳跃的思路提出了避免跳跃的图形标准，即通过绘制幅频响应跳跃与非跳跃的参数边界平面来优化力学参数。这种方案虽然得到了频响跳跃与非跳跃的临界条件，但是求解过程较复杂，有必要发展新的方法。

针对对称分段线性减振系统，本文基于约束分岔理论[10]，计算转迁集，确定系统可能的幅频响应类型，从而更细致地给出不同参数组合区域内的非线性振动特性；讨论在非跳跃区，阻尼比和激幅值对系统力传递率和系统幅频响应峰值点力传递率的影响，以及如何确定分段减振系统的特性参数，使其更好地发挥作用。

1 非线性动力学模型的建立

1.1 系统动力学模型

图1所示为对称分段线性弹簧系统，当振幅小于间隙时，只有主弹簧起作用，系统作线性振动；当振幅大于间隙时，质量块与副弹簧反复接触后又分离，因而系统的振动是非线性的。系统振动微分方程为

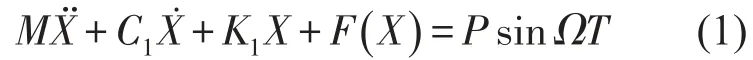
其中F(X)是弹簧非线性恢复力-位移函数

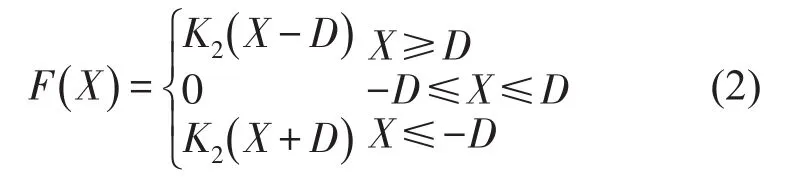
式中M为质量块质量，K1、K2为弹簧刚度，C1为弹簧阻尼，W、P分别为激振角频率和幅值，D为间隙值。

为得到振动方程的无量纲形式，引入如下变换及组合参数

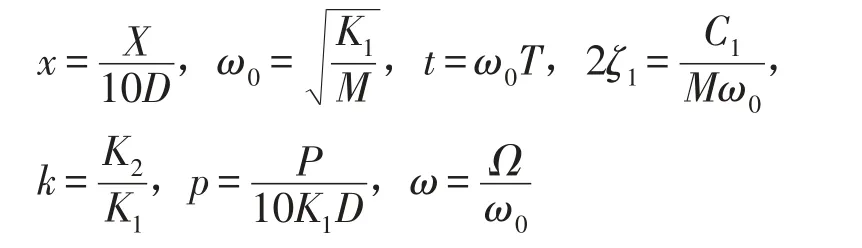
代入方程(1)和可得(2)

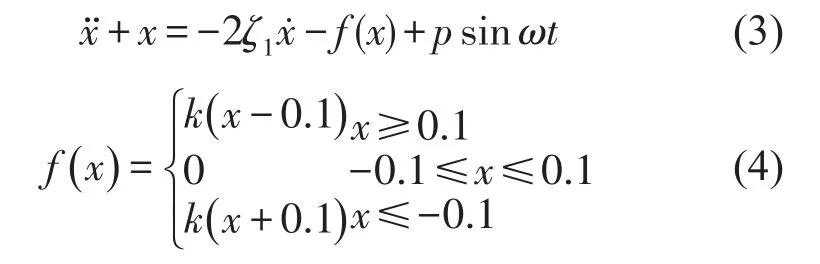
由于无量纲过程中特征长度选为十倍的间隙，使得无量纲间隙为0.1，这为系统主共振周期响应的近似分析奠定了基础。

1.2 平均法求取幅频响应方程

为考虑主共振(w=1)情况，将系统的振动方程改写为

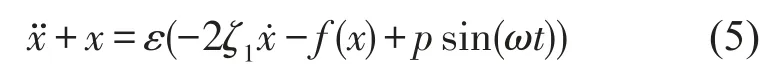
假设系统存在一次近似解形式如

其中j=wt+q，应用平均法[11]可将方程化成振幅、相位为未知量的标准方程，因振幅和相位的导数都是O(e)量级的周期函数，可代之以一个周期的平均值得到

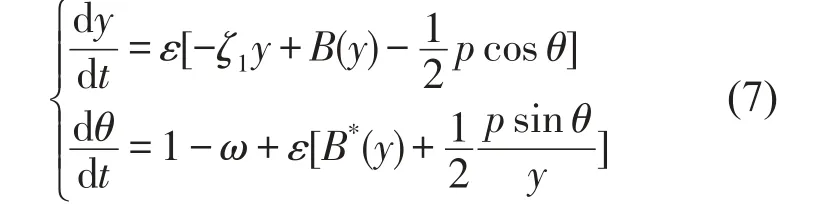
其中

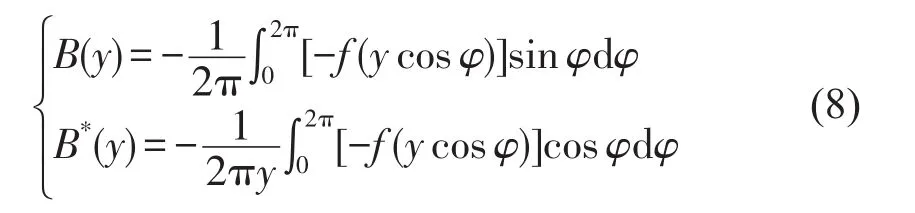
对于非线性系统，通常关心的是系统受迫振动的稳态值，于是令

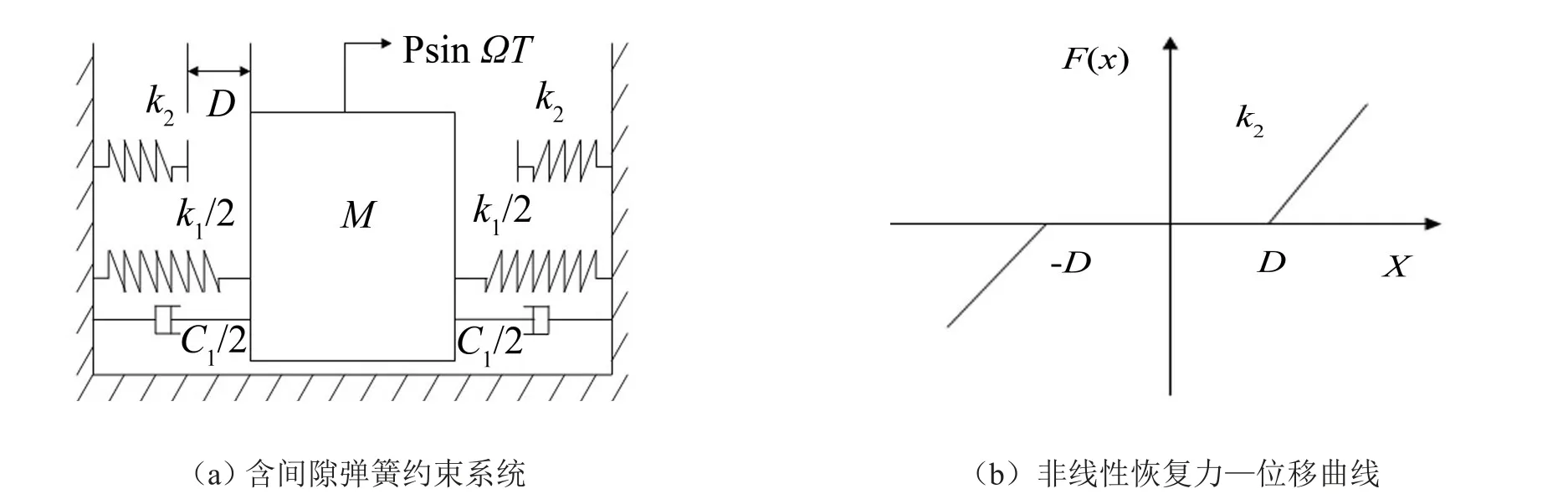
图1 动力学模型示意图

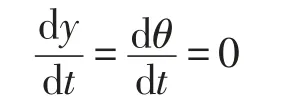
消除变量j，求得系统的稳态幅频响应方程为

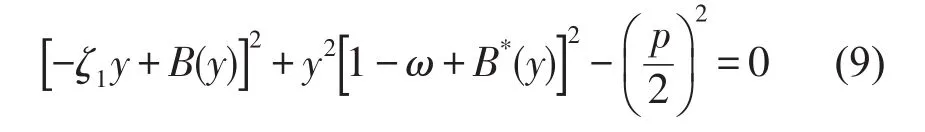
解出w可得

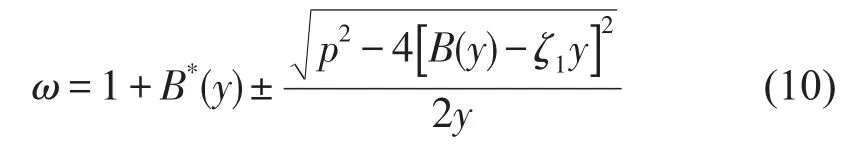
当系统参数给定时，由方程(9)或(10)可得幅频响应曲线。不同的参数值，可对应不同类型曲线，(也可能对应相同类型曲线)。为讨论参数对曲线类型的影响，奇异性方法是很好的工具。由于方程是分段的，因此要用约束分岔理论分析方法。

2 幅频响应分类及跳跃临界条件

为分析参数变化时，幅频响应曲线类型的变化，选择振幅y为状态变量，激励频率w为分岔参数，阻尼比z1和激励幅值p为开折参数，根据约束分岔理论可求得非空转迁集[8]包括

约束分岔集BI

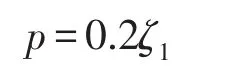
滞后集H

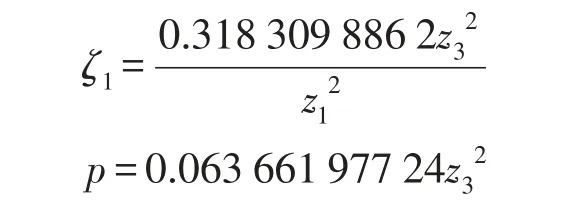
双极限点集DLI

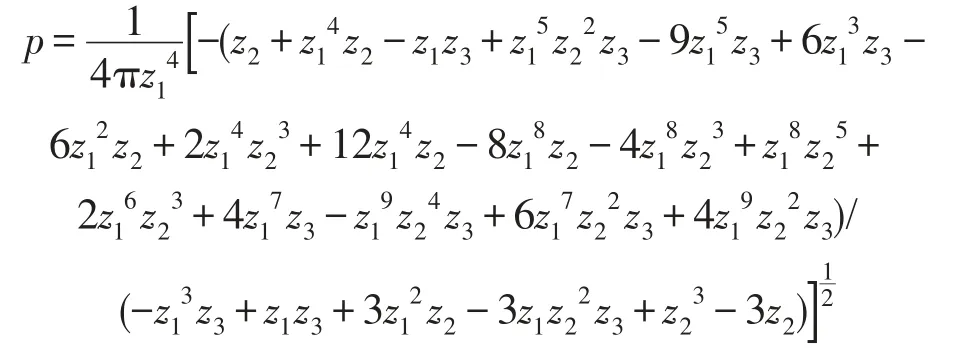
其中

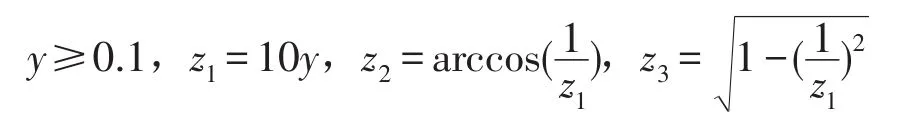
上述转迁集将无量纲参数空间划分为4个区域如图2所示。

根据奇异性理论，参数在同一个区域内取值时，幅频响应的定性特征是保持不变的，因而分别从不同区域内取一组(ζ1，p)值，画对应的分岔曲线，就得到参数变化时所有不同类型的分岔图(图3实线所示)，共有四种。在图3给出了幅频响应数值计算结果(图3星号所示)以便比较。显然数值结果与平均法结果吻合较好，说明基于平均法结果的后续分析是可靠的。

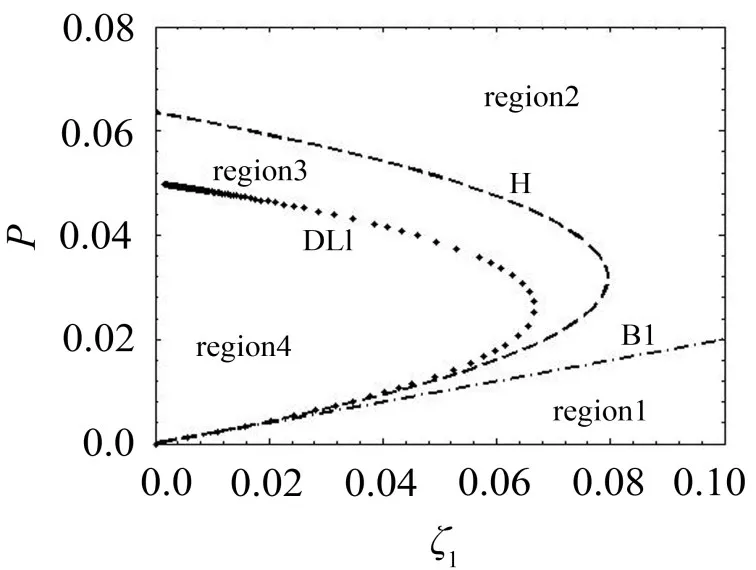
图2 转迁集(k=0.5)

综合以上分析可见，与文[7―9]采用的方法相比，分岔分析的奇异性方法更简便，并能得到更丰富的信息。

工程中为避免跳跃现象引起机械设备性能突变甚至破坏，就须在非跳跃区选择系统参数，也就是说在滞后集H右侧选择参数是避免跳跃的有效措施。激励强度增加时，非跳跃区向小阻尼方向扩展。跳跃现象只出现在较小阻尼、较小激励的情况下，因此适当增大阻尼，都可以防止激励强度更大时出现跳跃现象。

3 系统隔振效果分析

由约束分岔理论分析可知，在图2转迁集的非跳跃区域2取参数能保证分段减振系统充分发挥非线性弹簧作用，而且幅频响应不出现跳跃和滞后现象。

隔振系统对动态力的消减程度常用无量纲的力传递率来表示，即传递到基础上的力幅值与设备上激励幅值之比。由和可知传递到基础上的动荷载为

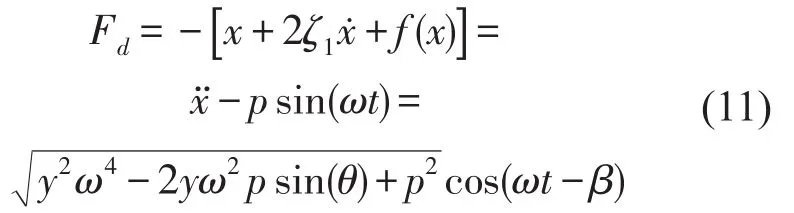
其中

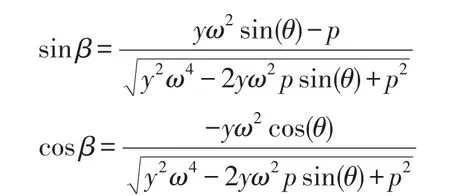
式中sin(q)由方程的第二式可确定为

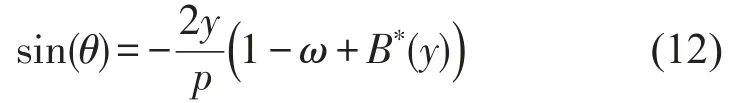
于是，传到基础上最大的动荷载值为

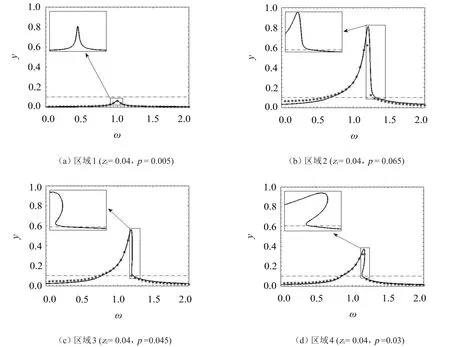
图3 不同类型幅频响应

非线性系统的力传递率为

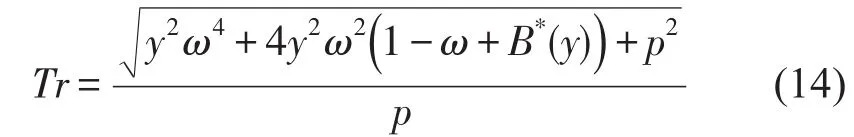
分别变化参数p、ζ1得到相应的Tr曲线，见图4。

当ζ1=0.09时，激励幅值系数p的变化对低频和高频区的力传递率都没有影响，对共振区有影响，此时共振峰逐渐增大，且峰值向右移。

当p=0.06时，随着阻尼比ζ1的增加，共振区的力传递率峰值迅速降低，阻尼比的影响逐渐减弱。

为分析幅频响应峰值点的力传递率，对方程(9)中的ω求一次导，得峰值点(ωm，ym)值

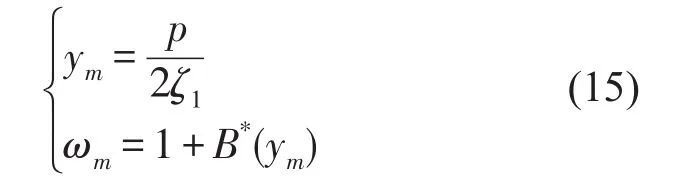
将(15)代入(14)，即求得幅频响应共振峰值点的传递率为

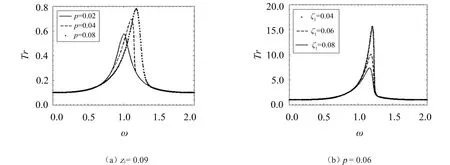
图4 参数p、z1分别对Tr的影响

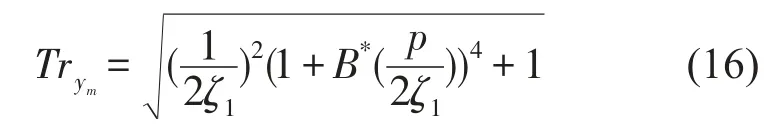
由此可绘制响应峰值点传递率关于阻尼比ζ1和激励幅值p变化的等高线图(图5所示)。结合转迁集图2，可在等高线图中绘制相应的非空转迁集，并且由前面约束分岔理论可知约束分岔集BI曲线将等高线图面分为线性部分与非线性部分。

由图5可见，当阻尼比取定值时，对于线性系统，激励幅值的增加对响应峰值点传递率没有影响；对于非线性系统，随着激励幅值的增加响应峰值点传递率先快速增大而逐渐趋向定值。

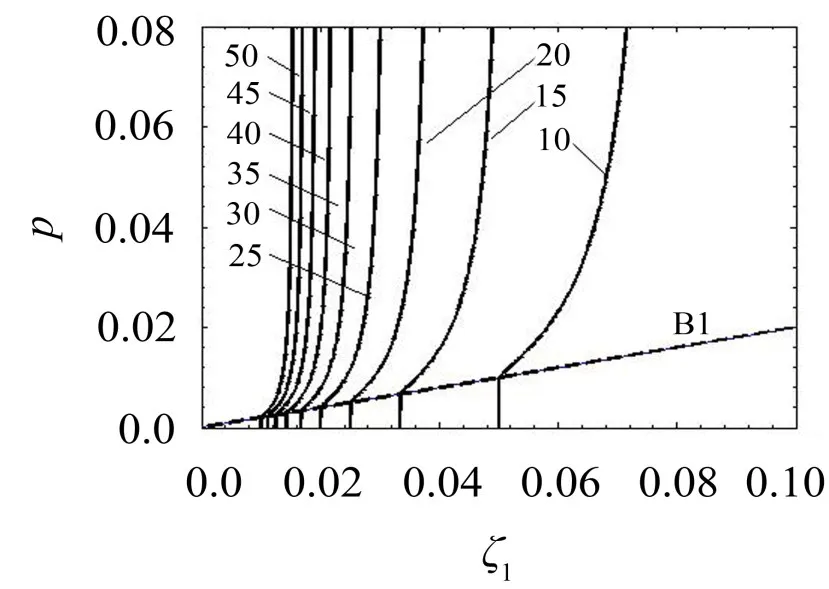
图5 等高线

4 结语

利用平均法理论、约束分岔理论分析了对称的分段线性弹簧系统的主共振响应，得到如下结论：

（1）利用约束分岔理论定性地分析系统可能发生的响应类型，更细致地划分了跳跃区的响应；

（2）得到系统产生跳跃的参数临界条件滞后集H，将开折参数平面分为跳跃区和非跳跃区，为系统设计提供了参考；

（3）阻尼比和激励幅值都对共振频率区的力传递率有影响，且在较小激励情况下，阻尼值越大，减振系统的抗振动性能越好。

［1］闻邦椿，李以农，韩清凯.非线性振动理论中的解析方法及工程应用[M].吉林：东北大学出版社，2001：294-303.

［2］胡海岩.分段线性系统动力学的非光滑分析[J].力学学报，1996，28(4)：100-105.

［3］闫政涛，翁雪涛，朱石坚，楼京俊.刚度分段线性系统的自由振动解析研究[J].噪声与振动控制，2010，30(6)：18-22.

［4］胡海岩.隔振系统限位器的非线性动力学设计[J].航空学报，1996，17(5)：18-22.

［5］钟顺，陈予恕.分段线性非线性汽车悬架系统的分岔行为[J].应用数学和力学，2009，30(6)：631-638.

［6］方益奇，王克军，张明.分段线性减振系统的振动性能分析[J].机械科学与技术，2011，30(2)：251-255.

［7］Jazar G N,Houim R,Narimani A,et al.Frequency response and jump avoidance in a nonlinear passive engine mount[J].Journal of Vibration and Control,2006, 12(11):1205-1237.

［8］Jazar G N,Mahinfalah M,Deshpande S.Design of a piecewise linear vibration isolator for jump avoidance[J].Proceedings of the Institution of Mechanical Engineers, Part K:Journal of Multi-body Dynamics,2007,221(3): 441-449.

［9］Deshpande,S.,S.Mehta and G.N.Jazar.Jump avoidance conditionsforpiecewiselinearvibrationisolator[C].Computer and Information in Engineering Conference.Long Beach,California USA.2005.

［10］吴志强，陈予恕.含约束非线性动力系统的分岔分类[J].应用数学和力学学报，2002，23(5)：477-482.

［11］陈予恕.非线性振动系统的分叉和混沌理论[M].北京：高等教育出版社，1993：330-370.

Analysis of JumpAvoidance and Vibration Reduction Performances of a Piecewise Linear Single DOF System

LEINa,WU Zhi-qiang

(School of Mechanical Engineering,Tianjin University,Tianjin 300072,China)

The damping performance of a single DOF system with piecewise linear terms under primary resonance excitation is studied.Employing the averaging method,an implicit function of the amplitude-frequency response equation under the primary resonance excitation is obtained.The transition sets can be calculated from this function on the basis of constraint bifurcation theory.The parametric critical condition to avoid jumping is calculated by qualitative analysis of the amplitude-frequency response equation in the sub-regions of the transition sets.Numerical calculation verifies the feasibility of this method.In addition,the influence of damping ratio and external excitation amplitude within the jump-free region on the global force transmissibility and the force transmissibility at the peak point of the amplitude-frequency response curve is discussed.The results show that under small excitation,large damping ratio can enhance the vibration resistance effect of the system.

vibration and wave;piecewise linearity;transition set;jumping;bifurcation;vibration reduction

10.3969/j.issn.1006-1335.2014.02.004

1006-1355(2014)02-0012-05

2013-03-06

国家自然科学基金：(11172198)；973项目：（2013CB035402）

雷娜(1987-)，女，湖南耒阳人，硕士，目前从事非线性振动、分岔与混沌方面研究。

E-mail:zhiqwu@tju.edu.cn