基于边光滑有限元法的结构振动与稳定性研究

李威，李诤，柴应彬，韩旭

（1.华中科技大学船舶与海洋工程学院，武汉430074；2.湖南大学机械与运载工程学院，长沙410082）

基于边光滑有限元法的结构振动与稳定性研究

李威1，李诤1，柴应彬1，韩旭2

（1.华中科技大学船舶与海洋工程学院，武汉430074；2.湖南大学机械与运载工程学院，长沙410082）

用一种新型的数值方法—边光滑有限元方法（edge-based smoothed finite element method,ES-FEM）对梁、板等简单结构的振动与稳定性问题进行分析与研究。光滑有限元方法在计算系统总体刚度矩阵时在构造的光滑域内对应变进行光滑操作，这样得到的刚度矩阵改善了有限元方法过刚的数值缺陷。对梁和板结构在一定边界条件下的振动与稳定性问题的分析结果表明：与其它有限元方法相比，光滑有限元方法提高了数值计算结果的精确度和收敛性。

振动与波；有限元法；边光滑有限元法；刚度矩阵；稳定性

Kay words:vibration and wave;FEM;ES-FEM;stiffness matrix;stability

梁和板结构是机械、车辆、土木、船舶等工业领域最基本的构件，它们的振动与稳定性关系到设备及整个系统的工作性能和寿命，严重时会使系统功能失效或者造成破坏事故，因此，对结构的振动和稳定性研究有重要的现实意义，而有限元方法作为重要的数值方法被广泛应用，其中三角形单元以其方便的前处理和对复杂几何形状的适应性，深受研究者的喜爱。然而，有限元三角形单元的发展深受精度和稳定性低的制约。应变光滑技术是CHEN[1]在节点积分无网格方法中为得到稳定解提出来的，很快被应用到自然单元方法。LIU[2―4]针对有限元方法(FEM)“过刚”的问题，将标准有限元方法和应力光滑技术结合起来提出了基于单元光滑有限元方法(SFEM)和基于节点光滑有限元方法(NS-FEM).与FEM“过刚”的特性正相反，NS-FEM表现出“过柔”的问题，而过柔的模型将会导致结果的不稳定性。针对此问题，LIU[5]提出一种基于边光滑有限元方法用于计算平面问题，展示了较好的计算性能。

本文基于边光滑有限元方法(ES-FEM)对梁、板等简单结构进行振动和稳定性分析,先将问题域离散为三角形单元，基于三角形的边进一步构造光滑域，在光滑域内运用应变光滑技术调整系统刚度，改善有限元方法过刚的模型缺陷，提高计算精度。

1 边光滑有限元法基本公式

1.1 光滑域的构造

在边光滑有限元法中，问题域Ω首先被离散成N个三角形单元，将每条边的端点和这条边相邻的两个单元的中心相连接，这样就在三角形单元的基础上形成了Nk个基于边的光滑域，如图1所示。

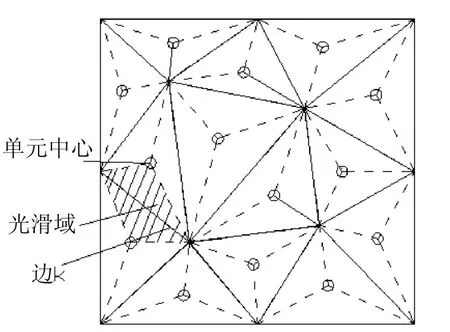
图1 三角形单元和基于边的光滑域

1.2 静力分析

对于平面应力问题，ES-FEM的静力平衡方程[5]为

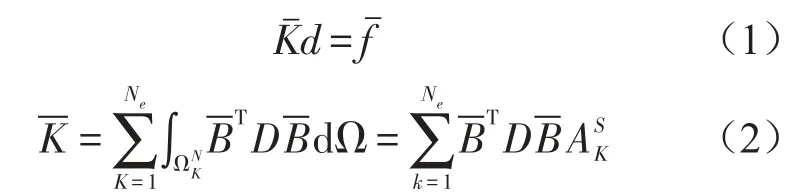
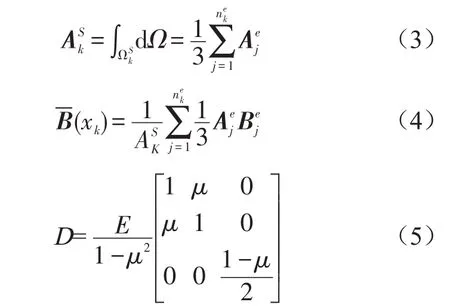
1.3 动力分析

平面问题的动力平衡方程可表示为

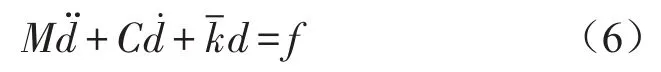
把d=d0exp(iwt)代入上式，不计阻尼和外力，可得到特征方程

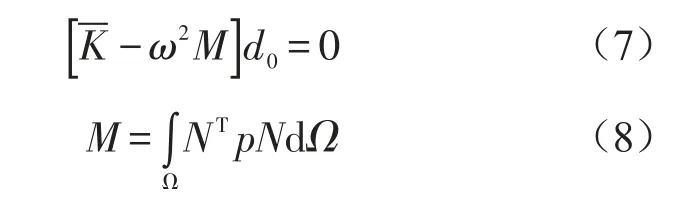
1.4 Reissner-mindlin板问题

设板离散成若干个三角形单元，每个单元有三个节点，每个节点有三个位移：每个节点的位移可表示为

自由振动分析的标准Galerkin弱形式[6]可表示为

对于板的小挠度屈曲，标准Galerkin弱形式[7]可表示为

由标准Galerkin弱形式可得板静力问题和屈曲问题的ES-FEM公式，导出特征值方程分别为

式中NS为光滑域的数目，为光滑域的面积，Ne为初始单元的数目，τ为板内初始应力矩阵，并且有

式中[8]k=5/6为剪切修正系数，α=0.05，h为三角形单元最长边的边长。对和有

式中Nj为第j个节点的形状函数。

2 数值算例

2.1 悬臂梁自由振动分析

考虑一悬臂梁模型，长L=120 mm,高H=12 mm,厚度t=1.0 mm，杨氏模量E=2.1×1011N/m2，泊松比υ=0.3，密度ρ=8×10-6kg/mm3。用单元尺寸为0.001m个节点的标准有限元方法结果作为参考，用Matlab软件编程实现FEM和ES-FEM，在单元尺寸为0.006 m和0.004 m的情况下分别对算例进行求解，前5阶固有频率如表1所示。

表1 悬臂梁自由振动前5阶固有频率

从表1可以很明显的观察到，当用同样的节点数目时，ES-FEM可以得到比FEM更精确的结果，收敛的更快。固有频率可以用来衡量结构的刚度，因此与FEM相比，用ES-FEM建立的模型更接近结构的精确刚度。用ES-FEM方法求悬臂梁自由振动前八阶模态振型如图2所示

2.2 Reissner-mindlin板自由振动分析

有一两端固支，两端自由的方形板，边长L=0.5 m，板厚t=0.002 5 m，材料杨氏模量E=2.0×1011N/m2，泊松比υ=0.3，质量密度ρ=8 000 kg/m3，采用2×20×20个三角形单元对板进行自由振动分析，用无量纲量表示结构的固有频率，这里D=Et3/(12(1-υ2))为板的弯曲刚度。求解结果和精确解[9]如表2所示。

图2 悬臂梁前8阶模态振型

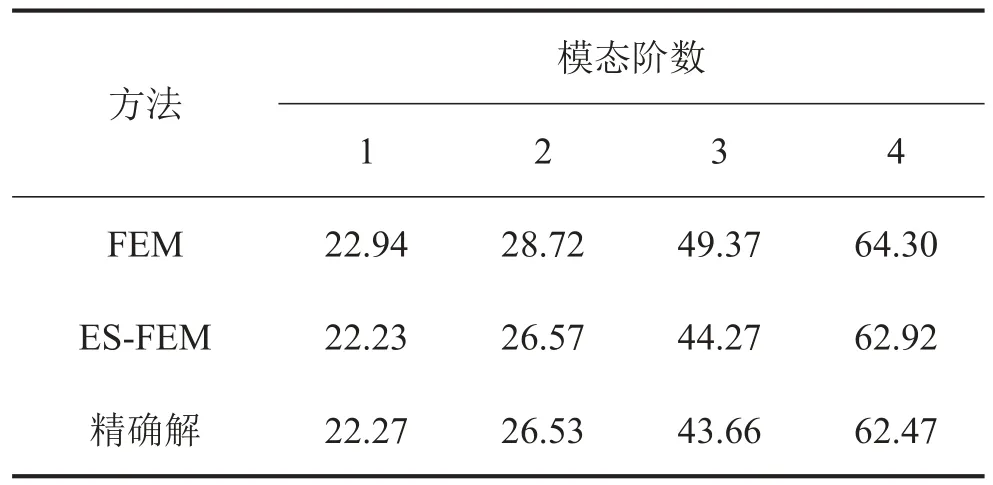
表2 方板自由振动前4阶无量纲频率

同精确解相比，在同样的节点数和单元划分条件下，ES-FEM方法得到的解比FEM更精确。用ESFEM方法求方板自由振动的前4阶模态振型如图3所示。

2.3 Reissner-Mindlin板稳定性分析

考虑一方形板，四边固支，单轴向受力，边长L=1 m，板厚t=0.01 m，材料杨氏模量E=2.0×1011N/m2，泊松比υ=0.3，定义屈曲载荷系数K=λcrL2/(π2D)，D为前例定义的弯曲刚度。分别用尺寸为0.1 m和0.05 m的三角形单元对板进行稳定性分析，解析解[10]为K=10.07，数值方法计算结果如表3所示。

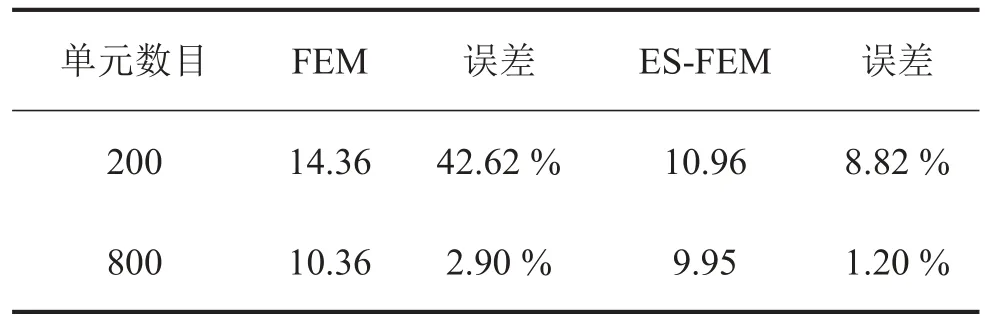
表3 方形板屈曲失稳载荷系数

用ES-FEM求得四边固支方形板轴向失稳模态如图4所示。

由FEM和ES-FEM的计算结果和解析解对照，可以明显的看出，在同样的单元划分条件下，与FEM相比，ES-FEM更接近精确解，在增加单元时收敛更快。

3 结语

本文采用一种新的边光滑有限元方法对梁、板等结构进行稳定性分析，在解析解的参照下将结果与标准有限元方法进行对比，结果表明：边光滑有限元方法有效地改善了标准有限元方法过刚的模型缺陷，在同样的单元条件下结果更为精确，收敛性更快更好，是一种比较理想的数值计算方法。

[1]CHEN J S,WU C T,YOON S,et al.A stabilized conformingnodalintegrationforGalerkinmeshfree method[J].International Journal for Numerical Methods in Engineering,2000,50:435-466.

[2]LIU G R,Nguyen T T,Dai K Y,et al.Theoretical aspects of the smoothed finite element method(SFEM)[J].InternationalJournalforNumericalMethodsin Engineering.2007,71(8):902-930.

[3]LIU G R,DAI K Y,Nguyen T T,et al.A smoothed finite elementmethodformechanicsproblems[J].Computational Mechanics,2007,39(6):859-877.

[4]LIU G R,A generalized gradient smoothing technique and smoothed bilinear form for Galerkin formulation of a wide class of computational methods[J].International Journal of Computational Methods.2008,5(2):199-236.

[5]LIU G R,DAI K Y,Nguyen T T.An edge-based smoothed finite element method(ES-FEM)for static,free and forced vibration analysis[J].Journal of Sound and Vibration, 2009,320:1100-1130.

[6]LIU G R,Quek S S.The finite element method[M]:A practical course.Butterworth Heinemann,Oxford,2002.

[7]Liew K M,CHEN X L.Buckling of rectangular Mindlin plates subjected to partial in-plane edge loads using the radial point interpolation method[J].International Journal of Solids and Structures.2004,41:1677-1695.

[8]Lyly M,Stenberg R,Vihinen T.A stablebilinear element for the Reissner-Mindlin plate model[J].ComputerMethodsinAppliedMechanicsand Engineering,1993,110:343-357.

[9]Leissa A W.Vibration of plates[M].Washington,DC, NASA,SP-160,1969.

[10]Timoshenko S P,Gere J M.Theory of elastic stability [M].3rd edition.New York,McGraw-Hill,1970.

[11]曾攀.有限元分析及应用[M].北京：清华大学出版社，2004.

Analysis of Vibration and Stability of Structures Using Edge-based Smoothed Finite Element Method

LIWei1,LIZheng1,CHAI Ying-bin1,HANXu2

(1.School of NavalArchitecture and Ocean Engineering,
Huazhong University of Science and Technology,Wuhan 430074,China; 2.College of Mechanical and Vehicle Engineering,Hunan University,Changsha 410082,China)

A novel numerical method,edge-based smoothed finite element method(ES-FEM),is used to analyze vibration and stability problems of beam and plate structures.In the ES-FEM,the system global stiffness matrix is computed using strain-smoothed method over the smoothing domains connected to the edges of the elements.As a result,the smoothing operation can reduce the over-stiffening behavior of the conventional finite element method.Numerical examples of beam and plate structures under special boundary conditions are presented to demonstrate that the ES-FEM can achieve higher accuracy and convergence rate compared with the conventional FEM for structures.

O241.82

ADOI编码：10.3969/j.issn.1006-1335.2014.02.001

1006-1355(2014)02-0001-04

2013-01-09

国家杰出青年科学基金项目（10725208）

李威（1975-），男，湖北武汉人，副教授，目前从事结构振动噪声分析与试验测试研究。

E-mail:hustliw@mail.hust.edu.cn