节理岩体巷道的稳定性分析

王 文，朱维申，陈云娟，张 磊

(山东大学 岩土与结构工程研究中心，山东 济南 250061)

节理岩体巷道的稳定性分析

王 文，朱维申，陈云娟，张 磊

(山东大学 岩土与结构工程研究中心，山东 济南 250061)

由于节理、断层等不连续面的存在造成岩体变形的不连续性，并且这些不连续面对岩体变形、应力等力学行为造成重要影响。对已有的非连续变形分析程序进行了两点改进，分别在程序中加入了锚杆的塑性模拟和改进的SSOR-PCG方法，并且通过与试验数据的对比验证了改进程序的正确性。分析了某节理岩体巷道围岩的破坏过程，得到在原来支护方式的基础上在顶拱应力集中的位置增加3根锚索的支护方式对巷道的支护效果较好。最后通过对巷道关键点位移的监测优化了支护参数，得到锚杆长度为 3 m，施加预应力为120kN为支护的最优方式。

节理岩体；围岩稳定性；非连续变形分析方法；锚固效应;裂隙扩展

目前，以有限元法和有限差分法为代表的计算方法在岩土工程稳定评价中广泛应用。但是，岩体作为一种地质结构体，这些基于连续介质的数值方法在模拟岩体的变形与稳定方面存在一定的局限性，因此，一些考虑岩体非连续性特点的数值方法，包括关键块体理论、离散元法、不连续变形分析方法等，自20世纪80年代开始逐步受到岩石力学界的关注和重视。非连续变形分析方法DDA(discontinuous deformation analysis)是由石根华博士提出的分析块体运动和变形的一种数值方法[1-2]，该方法基于最小势能原理建立系统方程，具有完备的块体运动学理论，能够较好地模拟多块体系统的大位移和大变形问题，因此在数值模拟和工程应用方面取得了较大的发展。郑榕明等详述了有限元与DDA的耦合算法，并给出了计算实例，证明了耦合方法的优越性[3];姜清辉[4]和刘君等[5]研究了三维DDA模型，编制了相应的 DDA 程序；邬爱清等[6]应用DDA对复杂地质条件下地下厂房围岩的变形与破坏特征开展了研究；马永政等[7]在DDA程序中引进无网格节点位移插值模式；姜清辉等[8]对DDA采用的常加速度法进行拓展，给出求解块体系统运动方程的 Newmark积分格式，并引入一种与块体不平衡力成正比的自适应阻尼，保证求解的稳定性；高亚楠等[9]采用有限变形理论对现有的DDA程序进行了改进，拓宽了DDA的使用范围；刘永茜等[10]在DDA中考虑了惯性力和阻尼力作用，并改进时间步长自动调节;焦玉勇教授等[11]改进了DDA方法，提出一种可用来模拟节理岩体的断裂破坏过程的新方法——DDARF(discontinuous deformation analysis for rock failure)。笔者对原有 DDARF程序进行了两点改进，方程迭代采用改进的SSOR-PCG方法进行，并且在程序中考虑了锚杆的塑性变形。应用改进的计算程序对某节理岩体巷道的支护方案和支护参数进行了优化分析，研究成果为正在开工的巷道的施工和设计者提供了参考。

1 DDARF的基本理论

DDARF方法是基于改进的DDA方法，用来解决断续节理岩体的破坏问题。该方法[12-13]采用行波法将计算区域自动剖分成三角形块体单元，块体边界分为真实节理边界和虚拟节理边界。对于模型中的所有节理，在没有达到断裂破坏准则时都将其定义为虚拟节理，其强度在计算过程中达到断裂破坏准则后则转化为真实节理，形成裂隙，并对其赋以真实的节理强度参数。裂纹扩展沿虚拟节理进行并且按照界面破裂准则进行开裂。虚拟节理的破坏分为拉伸破坏和剪切破坏两种，拉伸破坏采用最大拉应力准则，剪切破坏采用摩尔-库仑准则。断续节理的变形、破坏过程可认为是虚拟节理的开裂、扩展和贯通，在这一过程中伴随着虚拟节理力学属性(黏聚力、内摩擦角、抗拉强度)减弱、断续节理整体强度降低。因此，DDARF方法可以模拟裂纹萌生、扩展、贯通和岩体破碎全过程，适用于完整岩石、断续节理岩体乃至完全不连续岩体等任意情形。

2 锚杆的锚固效应

笔者对原来的锚杆模型进行了改进，考虑了锚杆的塑性。

2.1 锚杆的塑性模拟

对锚杆的数值模型做如下简化：① 锚杆主要承受轴向作用力。② 假定锚杆为理想弹塑性体，Tyield为锚杆的抗拉强度。当轴力fTanch，则置f=0。

考虑有一根锚杆连接块体i的点(x1，y1)与块体j的点(x2，y2)，如图1所示，设锚杆有预应力fa，锚杆的刚度为e。记锚杆长度为l，锚杆两端点位移分别为{u1，v1}和{u2，v2}，则

(1)

图1 锚杆示意Fig.1 Anchor schemes

锚杆的伸长量可表示为

y2)(dy1-dy2)]=

(2)

式中,lx，ly为锚杆的方向余弦，其表达式为

若锚杆有预应力，则锚杆的总伸长量为

(4)

则锚杆的应变能为

(5)

(6)

当f≥Tyield时，锚杆的势能Πb为

(7)

在程序中对锚杆进行判断，然后分别对式(6)，(7)求导使其最小化，叠加到总体平衡方程中即可以得到锚杆的锚固效应。

2.2 劈裂条件下裂隙试块的锚固效应

为了验证锚杆模型的正确与否，笔者对含裂隙的岩体进行了锚固，利用数值模拟方法对试块的强度和裂纹扩展过程进行了研究，然后与试验进行了对比分析。

2.2.1模型建立

张磊[14]对劈裂试验中锚固裂隙试块的强度和裂纹扩展过程进行了试验研究。参照他的试验，笔者拟采用DDARF程序进行数值模拟的相似研究，并与其结果进行对比分析。首先建立与劈裂试验有相同尺寸的模型并且施加相同的轴向位移荷载，然后分别研究锚固角(锚杆埋设方向与裂隙平面所形成的锐角)为30°，45°，70°和85°四种工况下的裂隙对试块性能的影响。为了使试验中的锚杆屈服，进而可以对比数值模拟和试验结果，程序中增加了计算时步，使锚杆进入了塑性区。

2.2.2数值模拟结果

使用DDARF程序模拟出锚固角度为30°的试块的轴向荷载-位移变化曲线。由于程序中不能模拟锚杆的滑移，因此试块破坏后轴向荷载-位移曲线中没有出现残余强度，如图2所示。锚固角度为30°的试块的裂纹扩展过程如图3所示：加锚后，试块首先在裂隙尖端产生翼裂隙，然后许多次生裂纹在两个相邻端开始产生并扩展，并且相向生长，随后形成破碎带而导致试块破坏。

图2 轴向荷载-位移曲线Fig.2 Axial load-displacement curves

图3 裂纹扩展过程Fig.3 Propagation process for fractures

2.2.3试验分析

张磊[14]研究了劈裂条件下不同锚固角度的锚杆对裂隙试件的锚固效应。试验中采用硬铝合金棒作为锚杆材料(图4(a))，并采用厚度为1mm，宽度为4cm，长度为15cm的聚氯乙烯薄膜加工的薄片作为预置贯穿裂隙(图4(b))。试块为边长100mm的立方体，裂隙与轴向的夹角分别为30°，45°，70°，85°。

图4 锚杆、裂隙材料和劈裂试验装置Fig.4 Anchor and fissure materials and splitting test device

劈裂试验是将试件放置于劈裂夹具中完成的(图4(c))。试验过程中采用位移控制方式，在伺服压力机上以一定的加载速率对劈裂夹具加载，直至试件发生劈裂破坏。

2.2.4试验结果

通过劈裂试验分别得到锚固角度为30°的试块轴向荷载-位移变化曲线和破坏过程，如图5和6所示(图6中的圆圈表示锚杆)。图5中的轴向荷载峰值点A的值见表1。试块破坏过程如下：随着荷载的增大，裂缝发展程度增加，随后锚杆与砂浆在黏结界面上发生滑移，锚杆屈服，最后试件彻底断裂。

图5 劈裂试验中轴向荷载-位移曲线Fig.5 Axial load-displacement curve in splitting test

图6 试验中裂纹扩展过程Fig.6 Crack propagation process in splitting test

表1 锚固试块的峰值强度Table 1 Peak strength of anchor specimens

2.2.5结果对比分析

将DDARF数值模拟计算结果与室内劈裂试验结果进行对比，见表1(括号中的数值表示该数据比试验数据的减少量占试验数据的百分比)可知：轴向荷载-位移曲线的峰值强度相差幅度在1%～15%，模拟效果较好。同时，数值模拟的裂纹扩展规律也与试验现象相符。由表1也可以得到锚杆的塑性模型可以更加精确地模拟锚杆对节理岩体的加固作用，表明这种方法对锚杆的模拟是正确的。

3 改进的SSOR-PCG方法

最初非连续变形方法方程迭代采用了直接解法和逐步超松弛(SOR)迭代法。块体较少时，可采用直接解法，块体较多时，采用SOR迭代法。SOR法需要一个松弛因子，它的选取对计算效率是至关重要的，但是最佳的松弛因子又无法确定，这无疑影响了非连续变形方法的使用。考虑到平衡方程中K阵的对称、正定、主元占优的特点，笔者采用预处理共轭梯度法(PCG)，用K阵的对角阵作为预处理矩阵。如果将PCG与SSOR(对称逐步超松弛)相结合，可以得到非常有效的SSOR-PCG法。它具有SSOR对松弛因子的不敏感性和PCG收敛速度快的特点。笔者将改进后的SSOR-PCG方法[15]加入到DDARF程序中，节省了方程的计算量，加快了计算效率，可比原迭代方法节省计算量8%～50%[16]。

4 工程中的实际应用

在煤矿巷道支护工程中，支护方式的选择及支护参数的确定往往是重点考虑的问题，可以达到提高支护效果的目的，对煤矿节省成本，提高经济效益，具有重要应用价值。现以某煤矿的水平运输大巷为例，利用改进后的数值模拟软件DDARF研究了巷道围岩的裂纹扩展过程，改进了支护方式，优化了支护参数，为现场的施工与设计提供了一定的理论指导。

4.1 模型的建立

煤矿的半圆拱形巷道断面外接于半径为1.5m 的圆。巷道问题符合平面应变问题，故建立平面模型进行模拟，选取煤矿巷道比较有代表性的局部区域进行模型计算，模型的宽、高分别是巷道宽、高的10倍。模型的上表面施加均匀的垂直压应力，模型两侧面施加随深度变化的水平压应力，模型下表面的垂直和水平位移固定。该大巷围岩在开挖后出现破裂岩体，主要以泥岩、粉砂岩为主，并夹有多层小煤及煤线，而且附近还有小断层，岩层非常破碎。因此笔者根据地质条件，运用蒙特卡洛方法，生成随机节理，推演了更小规模的节理的空间分布。巷道模型和加载方式如图7所示。

图7 巷道的计算模型和加载方式Fig.7 The computation model and load method of the roadway

4.2 力学参数和收敛准则

在岩体工程稳定性分析中，力学参数选取将对计算结果产生很大的影响，本次计算模型力学参数根据现场位移反分析所得结果，并参考岩块试验得到，见表2,3。

表2岩体力学参数
Table2Mechanicalparametersoftherockmass

名称弹性模量/GPa泊松比内摩擦角/(°)黏聚力/MPa容重/(kN·m-3)中粒粗砂岩3 80 2130225 4粉砂岩1 60 27271 725 0煤0 70 35200 415 6泥页岩0 80 32251 321 0细砂岩3 20 23293 225 3

表3岩体界面的力学参数
Table3Mechanicalparametersoftheinterfaceoftherockmass

内摩擦角/(°)黏聚力/MPa抗拉强度/MPa3021

4.3 巷道支护方案的优化

4.3.1巷道围岩的破坏过程

采用屏幕录像专家软件记录DDARF程序计算过程，得到直墙半圆拱形巷道围岩的破坏过程，如图8所示：在巷道底板处，随着底角破坏程度的增加，底板跨度不断增大，引起底板变形。然后巷道底角处破坏，引起两帮承载能力降低，进而导致顶板变形量加大。同时数值模拟和工程实际情况均表明巷道围岩两帮及顶底板位移量并不是均匀的，而是首先从巷道某一个部位开始破坏，从而导致整个巷道支护体失稳，直墙半圆拱巷道周围形成“双耳”是应力集中关键部位。

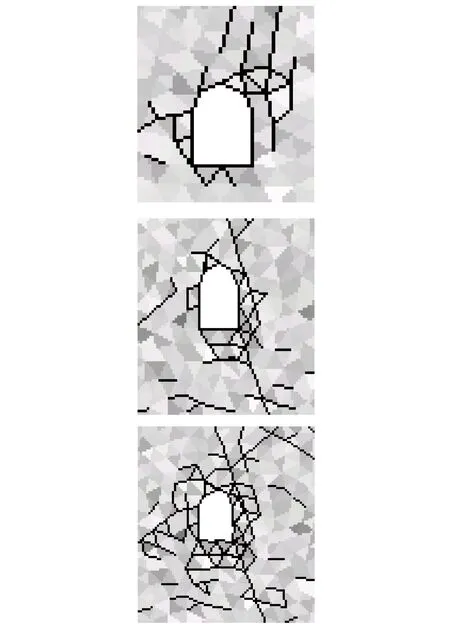
图8 围岩的破坏过程Fig.8 The damage process of surrounding rocks

4.3.2巷道支护方式优化

由于受断层影响，局部地段顶煤节理裂隙发育，帮顶围岩松软易碎，顶板及肩角处下沉明显，围岩产生不连续变形(图8)。根据巷道的破坏过程，原设计中采用锚杆支护，如图9(a)所示。其中锚杆采用φ25mm的强力锚杆，长度为3 m，弹性模量为200GPa，预应力为120kN，屈服强度600MPa。施加锚杆后，边墙和顶部的位移都减小，但是顶板的应力集中程度也是比较高，底板无支护，造成底臌。笔者在原设计的基础上改变了巷道围岩的支护方式，采取在顶部应力集中关键点上施加锚索(图9(b))。其中锚索采用直径19mm的钢绞线，极限拉断力400kN，长度为6 m。3根锚索的功能各不相同，中间锚索是控制顶板位移的，而两边的锚索是转移上覆岩层应力到深部去；底角锚杆是控制底臌的，它能有效控制巷道两帮的水平挤压力，从而有效控制底臌。由图9可知施加锚索后，巷道周边的应力集中现象得到改善，应力分布更加均匀，表明锚索调动了深部岩体强度，控制了浅部岩体的稳定性。

图9 巷道支护和破坏Fig.9 The diagrams of support of roadways and damage

不同支护方式下关键点的位移值见表4(括号中的数值表示该数据比无锚杆数据减少量占无锚杆数据的百分比)。可以看出：加锚杆后，巷道的顶拱、帮部和底板的位移值都比无锚支护时位移值小，减小幅度为10%～20%；锚杆锚索联合支护后，巷道的顶拱、帮部和底板的位移值比无锚支护时的减小20%～30%。由此可见当锚杆、锚索的预应力产生协同作用时，对深部巷道的支护效果明显，有效地阻止了巷道围岩的变形，控制了巷道的破坏。因此，锚杆-锚索-围岩共同承载的支护方式可以维护巷道的安全稳定，值得推广。

表4不同支护方式下关键点的位移
Table4Comparisonofdisplacementsofkeypointsmm

工况顶拱左帮中点底板中点无锚杆-1085146 3锚杆效应-92(14 8%)43(15 7%)40(13 6%)锚杆锚索效应-80(25 9%)37(27 5%)36(22 2%)

4.3.3支护参数的优化

(1)锚杆预应力值的选择。

在基本模型其他参数不变的条件下，通过改变锚杆和锚索的预应力值[17](60，90，120，150，180kN)得到其对巷道围岩位移的影响变化曲线，如图10(a)所示。

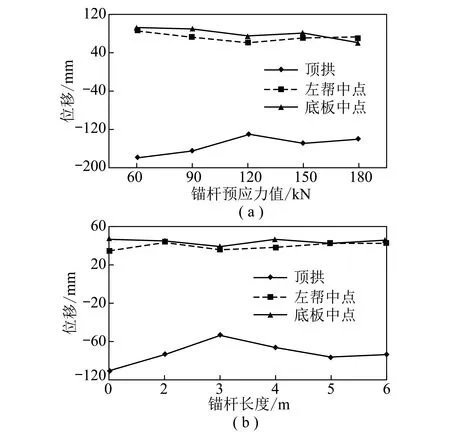
图10 锚杆预应力，锚杆长度与位移关系曲线Fig.10 Relation curves of prestress and length of the rock bolt with displacement

由图10(a)可见，随着锚杆预应力的增加，围岩的位移值减小，但是预应力值为120kN后再增加预应力值围岩的位移量的改变不是很大，所以在本工程中施加预应力为120kN比较合适。

(2) 锚杆长度的选择。

在基本模型其他参数不变的条件下，通过改变锚杆长度(2，3，4，5，6 m)得到其对巷道围岩位移的影响变化曲线，如图10(b)所示。

由图10(b)可见，锚杆长度影响着地下工程位移量及围岩稳定性，且锚杆长度为3 m时围岩的位移较小。锚杆长度若再增大，将造成浪费，而且也不必要，所以在本工程中锚杆长度为3 m比较合适。

5 结 论

(1)在劈裂试验中，通过DDARF数值模拟与室内试验进行对比得到：荷载-位移曲线的峰值强度较一致，数值模拟的裂隙扩展规律也与试验现象相符。同时通过试验验证了锚杆塑性模型的正确性，可以更加精确的模拟锚杆对节理岩体的加固作用。

(2)采用位移收敛准则计算某个工程收敛的时间和收敛时步，得到改进的SSOR-PCG收敛方法可以节省方程的计算量，加快计算效率，大大的提高程序的计算速度。

(3)巷道围岩采用锚杆-锚索-围岩共同承载的支护方式，对深部巷道的支护效果明显，控制了巷道的底臌，改善了巷道周边的应力集中，并且减少了巷道围岩的变形。

(4)通过对巷道支护参数的优化分析，本工程中选取锚杆长度3 m，施加预应力为120kN比较合适，巷道围岩的稳定性较好。

[1] Shi G H.Discontinuous deformation analysis:a new numerical model for the statics and dynamics of block system[D].Berkeley：University of California,1988.

[2] Chang T C.Nonlinear dynamic discontinuous deformation analysis with finite element meshed block systems[D].Berkeley:University of California,1994.

[3] 郑榕明，张勇慧，王可钧.耦合算法原理及有限元与DDA 的耦合[J].岩土工程学报,2000,22(6):727-730. Zheng Rongming,Zhang Yonghui,Wang Kejun.Coupling of FEM and DDA method[J].Chinese Journal of Geotechnical Engineering,2000,22(6):727-730.

[4] 姜清辉.三维非连续变形分析方法的研究[D].武汉:中国科学院武汉岩土力学研究所,2000.

[5] 刘 君.三维非连续变形分析与有限元耦合算法研究[D].大连:大连理工大学,2001.

[6] 邬爱清,丁秀丽,陈胜宏,等.DDA 在复杂地质条件下地下厂房围岩变形与破坏特征分析中的应用研究[J].岩石力学与工程学报,2006,25(1):1-8. Wu Aiqing,Ding Xiuli,Chen Shenghong,et al.Researches on deformation and failure characteristics of an underground powerhouse with complicated geological conditions by DDA method[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(1):1-8.

[7] 马永政,郑 宏,李春光.应用自然邻接点插值法的块体非连续变形分析[J].岩土力学,2008,29(1):119-124. Ma Yongzheng,Zheng Hong,Li Chunguang.Applying natural neighbor interpolation to discontinuous deformation analysis of block system[J].Rock and Soil Mechanics,2008,29(1):119-124.

[8] 姜清辉，周创兵，漆祖芳.基于Newmark积分方案的DDA方法[J].岩石力学与工程学报,2009,28(1):2778-2783. Jiang Qinghui，Zhou Chuangbin，Qi Zufang.Discontinuous deformation analysis method besed on newmark integration algorithm[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(1):2778-2783.

[9] 高亚楠，高 峰，Man-chu Ronald YEUNG.基于有限变形理论的非连续变形分析方法改进[J].岩石力学与工程学报,2011,30(11):2360-2365. Gao Yanan，Gao Feng，Man-chu Ronald YEUNG.Modification of discontinuous deformation analysis method based on finite deformation theory[J].Chinese Journal of Rock Mechanics and Engineering,2011,30(11):2360-2365.

[10] 刘永茜，杨 军.一种改进步长自调的非连续变形分析法[J].岩土力学,2011,32(8):2544-2548. Liu Yongqian,Yang Jun.An improved DDA method with adaptive step size[J].Rock and Soil Mechanics，2011,32(8):2544-2548.

[11] 焦玉勇，张秀丽，刘泉声,等.用非连续变形分析方法模拟岩石裂纹扩展[J].岩石力学与工程学报,2007,26(4):682-691. Jiao Yuyong,Zhang Xiuli,Liu Quansheng,et al.Simulation of rock crack propagation using discontinuous deformation analysis[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(4):682-691.

[12] 张秀丽.断续节理岩体破坏过程的数值分析方法研究[D].武汉:中国科学院武汉岩土力学研究所,2007.

[13] 张秀丽,焦玉勇,刘泉声,等.用改进的DDA方法模拟公路隧道的稳定性[J].岩土力学,2007,28(8):1710-1714. Zhang Xiuli,Jiao Yuyong,Liu Quansheng,et al.Modeling of stability of a highway tunnel by using improved DDA method[J].Rock and Soil Mechanics,2007,28(8):1710-1714.

[14] 张 磊.锚杆加固对裂隙岩体力学性能影响的室内试验和数值分析[D].济南:山东大学,2009.

[15] 林绍忠.对称逐步超松驰预处理共轭梯度法的改进迭代格式[J].数值计算与计算机应用,1997,18(4):266-270. Lin Shaozhong.Improved iterative format of symmetric successive over relaxation-preconditioned conjugated gradient mthod[J].Journal of Numerical Methods and Computer Applications,1997,18(4):266-270.

[16] 林绍忠.用预处理共轭梯度法求解有限元方程组及程序设计[J].河海大学学报,1998,26(3):112-115. Lin Shaozhong.Application of preconditioned conjugated gradient method to finite element equations and program design[J].Journal of Hehai University,1998,26(3)：112-115.

[17] 康红普，姜铁明，高富强.预应力锚杆支护参数的设计[J].煤炭学报,2008,33(7):721-726. Kang Hongpu，Jiang Tieming，Gao Fuqiang.Design for pretensioned rock bolting parameters[J].Journal of China Coal Society,2008,33(7):721-726.

Analysisofroadwaystabilityinjointedrockmasses

WANG Wen,ZHU Wei-shen,CHEN Yun-juan,ZHANG Lei

(GeotechnicalandStructuralEngineeringResearchCenter,ShandongUniversity,Jinan250061,China)

The mechanical behaviors of the jointed rock masses of the roadway were simulated using discontinuous deformation analysis(DDA).Two improvements were developed,which respectively the anchor plastic simulation and improved SSOR-PCG method were implemented into the original DDA program and the advanced program was justified through the comparison with experimental data.Then,the process of damage of the surrounding rocks of the roadway was simulated using the advanced program and supporting method was optimized.At the last,the displacement monitor results of the key points were studied and applied to investigate the optimal support pattern of the roadway,which showed the anchor length with 3 m and the prestressing with 120kN was the optimal support method.

jointed rock masses;surronding rock stability;DDA(discontinuous deformation analysis);anchorage effect;crack propagation

10.13225/j.cnki.jccs.2013.0183

国家自然科学基金重点资助项目(41072234)

王 文(1982—)，女，山东济宁人，博士研究生。E-mail：sddxww@126.com。通讯作者：朱维申(1932—)，男，教授，博士，博士生导师。E-mail：zhuw@sdu.edu.cn

TD322.4

A

0253-9993(2014)01-0057-07

王 文，朱维申，陈云娟，等.节理岩体巷道的稳定性分析[J].煤炭学报,2014,39(1):57-63.

Wang Wen,Zhu Weishen,Chen Yunjuan,et al.Analysis of roadway stability in jointed rock masses[J].Journal of China Coal Society,2014,39(1):57-63.doi:10.13225/j.cnki.jccs.2013.0183