广义积分型Cauchy中值定理及其逆定理

刘丽娜

(徐州经贸高等职业学校 公共基础部,江苏 徐州 221004)

0 引言

积分中值定理在微积分理论中占有极其重要的地位,有着十分广泛的应用,而Cauchy中值定理,特别是Lagrange中值定理,长期以来一直是人们研究的主要内容。文献[2、4]给出了 广义Cauchy中值定理及其在凸函数条件下的逆定理，文献[1]讨论了定积分中值定理的推广,分别给出了广义Lagrange中值定理及其逆定理,讨论了凸函数的微分中值定理的反问题,给出了积分型Cauchy中值定理的推广形式，本文对积分型Cauchy中值定理进行了进一步的研究，给出了广义积分型Cauchy中值定理及其逆定理的相关结论。

定理1 (积分型Cauchy中值定理)若

(i)f(x),g(x)在[a,b]内连续;

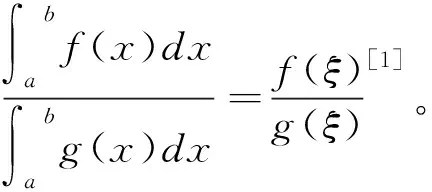
定理2 (广义Cauchy中值定理)设

(i)f(x)在[a,b]上连续，且f'+(x),f'-(x)存在；

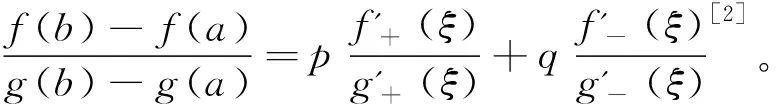
定理3 (广义Cauchy中值定理逆定理)设

(i)f(x)为[a,b]上单调递增凸函数;

(ii)g(x)为凹函数;

(iii)g(x)在(a,b)内可导,且g'(x)≠0;

则对于∀ξ∈(a,b)及非负数p、q且p+q=1，一定存在α、β∈(a,b),使得

定义1 设f(x)为定义在区间I上的函数,若对I上任意两点x1、x2和实数ξ∈(0,1),总有f(ξx1+(1-ξ)x2)≤ξf(x1)+(1+ξ)f(x2)，则f(x)称为区间I上的凸函数。若式中不等号反向,则称f(x)为区间I上的凹函数[3]。

1 引理

引理1 设f(x)在[a,b]上连续,f'+(x),f'-(x)存在,且f(a)=f(b)，则在(a,b)内至少存在一点ξ及非负数p、q且p+q=1,使得pf'+(ξ)+qf'-(ξ)=0[4]。

引理2 设f(x)为[a,b]上单调递增的凸函数,g(x)为[a,b]上的严格单调递增的凹函数,则对于[a,b]上的任意三点a≤x1≤x2≤x3≤b，下式成立：

引理3 设①f(x)为[a,b]上的单调递增凸函数;②g(x)为[a,b]上严格单调递增的凹函数; ③g'(x)>0,x∈(a,b),则∀x0∈(a,b) 有

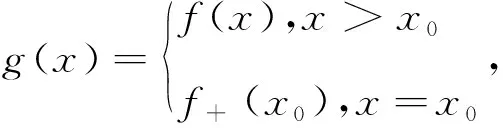
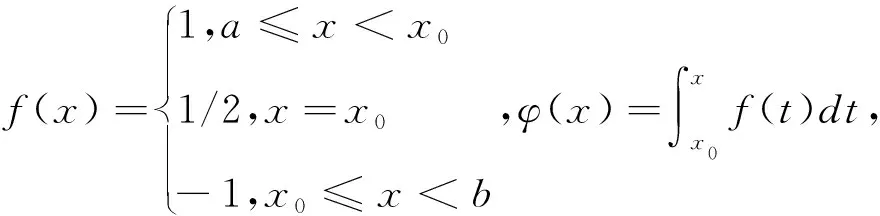
2 主要结论与证明

定理4 (广义积分型Cauchy中值定理) 设

(i)f(x)在[a,b]上可积，且f+(x),f-(x)存在；

(ii)g(x)在[a,b]上连续,且g(x)≠0；

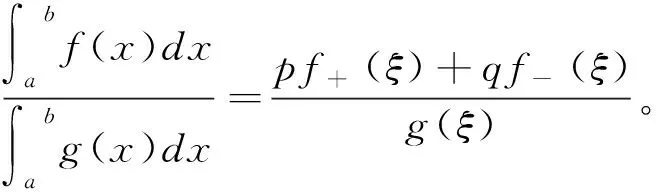
由于f+(x)、f-(x)存在,且g(x)在[a,b]上连续,由引理4可知

(3)

(4)

又易验证φ(a)=φ(b)。根据引理1,至少存在一点ξ∈(a,b)及非负数p、q,且p+q=1,使得pφ'+(ξ)+qφ'-(ξ)=0。注意到g(x)在[a,b]上连续,且g(x)≠0,从而有

(5)

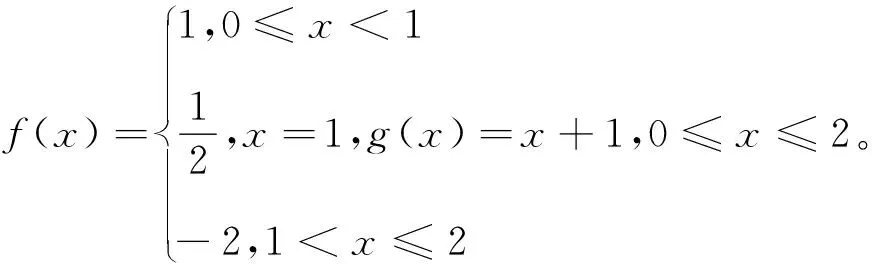
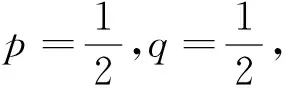
定理5 (广义积分Cauchy中值定理的逆定理)

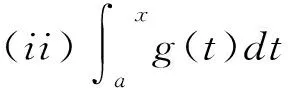
(iii)g(x)在[a,b]上连续,且g(x)>0。

则对于∀ξ∈(a,b)及非负数p、q,且p+q=1,一定存在α、β∈(a,b),使得

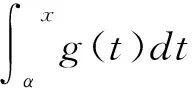
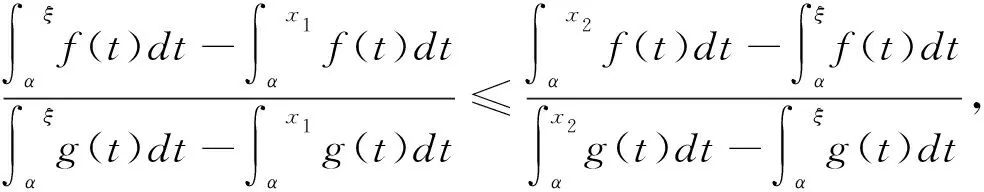
由引理3知：

于是对于非负数p、q且p+q=1,有

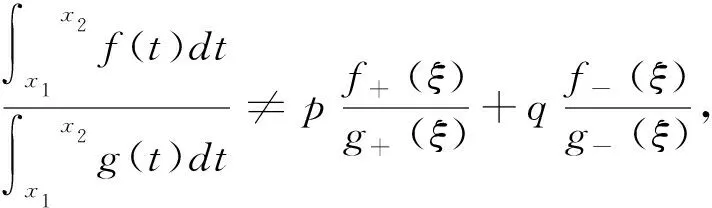
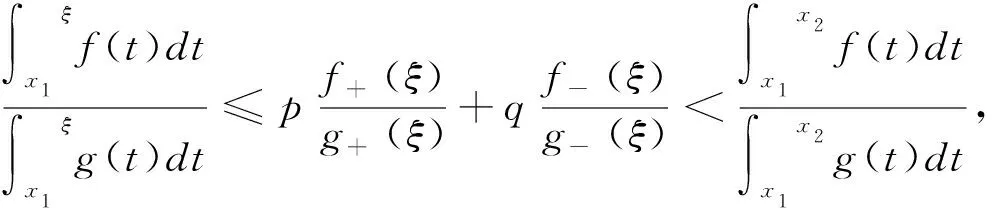
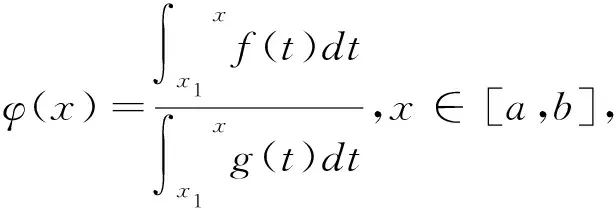
令α=x1，β=x0,故定理成立。

参考文献:

[1] 严振详.定积分中值定理的推广[J].上海海运学院学报,1995,16(1):29-33.

[2] 刘孝书,郭致林.广义Cauchy中值定理及其逆定理[J].数学的实践与认识,2006,36(6):337-340.

[3] 陈传璋.数学分析(上册)[M].北京:高等教育出版社,1983.

[4] 刘昌茂.广义Cauchy中值定理[J].吉首大学学报,1998,19(4):72-74.