A Localization Algorithm for Wireless Sensor Networks with Asymmetric Links*

ZHANG Yaming，SHI Haoshan*，LIU Yan，CHENG Wei

(1.School of Electronics and Information，Northwestern Polytechnical University，Xi’an 710072，China; 2.National Key Lab.of Antennas and Microwave Technology，Xidian University，Xi’an 710071，China)

A Localization Algorithm for Wireless Sensor Networks with Asymmetric Links*

ZHANG Yaming1，SHI Haoshan1*，LIU Yan2，CHENG Wei1

(1.School of Electronics and Information，Northwestern Polytechnical University，Xi’an 710072，China; 2.National Key Lab.of Antennas and Microwave Technology，Xidian University，Xi’an 710071，China)

For conquering the problem of poor locating performance by using DV-Hop algorithm in the complex environment with asymmetric links.Several approaches were put forwarded in this paper.Firstly，a neighbor nodes mining method is used for ensure the accurate identification of adjacent nodes.Secondly，the minimum hop-count mechanism is used for calculate the real hop count between nodes.Thirdly，a new method of computing average hop-size is adopted to reduce its error.And then，a novel method of solving a system of equations is presented to estimation the initial location of unknown node.Finally，a coordinate calibration technology is used to further improve the positioning accuracy.Simulation results show that，the improved algorithm can effectively avoid the influence of asymmetric links，significantly improve the positioning accuracy and reduce the cost of network.

wireless sensor networks(WSNs);localization;DV-Hop algorithm;asymmetric links

随着无线传感器网络应用的日趋复杂和多样化，作为其关键技术的节点定位技术得到了国内外学者的持续关注和研究。按照是否需要测量节点间距离，现有定位算法可分为基于测距的(Range-Based)定位和无需测距的(Range-Free)定位两类［1］。Rangebased定位首先使用测距技术获得节点间距离或角度信息，然后使用三边测量法、三角测量法或极大似然估计法计算未知节点坐标。这种定位机制虽然定位精度较高但通常需要配备额外的特殊硬件设备，会造成较大的成本和能耗负担。Range-free定位不需要测量节点间距离或方位，仅依靠相邻节点间的连通关系或利用节点间的估计距离计算节点位置。如今，随着Range-Free定位算法在成本控制等方面优势的进一步体现，它已经被视为一种高性价比的、简单易行且定位精度可接受的定位方式而倍受重视。DV-hop算法［2］作为无需测距定位算法的典型代表，是目前应用最广泛的定位算法之一，有着极其重要的研究价值。随着无线传感器网络研究和应用的进一步深入，针对DV-Hop算法的改进研究倍受重视。然而多数文献［3-10］局限于对个别问题的研究改进，缺乏对整个网络系统的全面考虑，更很少考虑真实环境，特别是复杂环境中存在的大量不对称链路对DV-Hop算法的影响。文献［11］通过对由26个节点组成的无线传感器网络进行链路质量测量，验证了无线传感器网络中的通信链路存在不对称性。文献［12］对无线传感器网络中链路存在不规则性进行了更深入的分析，发现导致链路不规则的原因有两大类，即传输介质(如介质类型、噪声和温度、障碍物等)和设备(如天线类型和增益、发射功率、接收机门限值等)。文献［13］通过对密集传感器网络的研究表明，数据报文接收率在真实环境中会随时间和空间因素变化，大约有5%到15%的链路是不对称链路，且环境约复杂不对称链路比例越高。这种不对称链路会严重影响DV-Hop定位算法中平均跳距和节点间距离的估算，进而影响到算法的定位精度。

鉴于以上研究和分析，本文提出了一种可用于复杂环境的改进的DV-Hop定位算法。该算法首先采用邻居挖掘机制确保相邻节点之间能准确识别，然后利用最小跳数方法更准确的计算未知节点到每个信标节点的最小跳数;接着采用改进的平均跳距计算方法减小平均跳距误差;然后采用一种新的方程组求解方法完成节点初步定位;最后使用一种简单的坐标校准技术，进一步提高定位精度。

1 DV-Hop算法原理

DV-Hop算法［2］是由美国路特葛斯大学Niculescu等人提出的类似于传统网络中距离向量路由机制的一种免测距无线传感器网络定位算法。其过程可分3个阶段，简单描述如下:

第1阶段通过典型的距离矢量交换协议使每个节点获取到每个锚节点的最小跳数。

第2阶段计算未知节点与锚节点之间的距离。在此阶段，每个锚节点根据第1阶段中记录的其它锚节点的位置信息和相距跳数，利用式(1)估算出平均跳距HopSize。然后，将该平均跳距作为校正值通过带有生存期字段的分组广播至网络中，未知节点仅存储接收到的第1个校正值，并转发给邻居节点，忽略所有后收到的校正值。未知节点接收到平均跳距后乘以其到锚节点的最小跳数，即可得到其与相应锚节点之间的估计距离(利用跳段距离代替直线距离)。

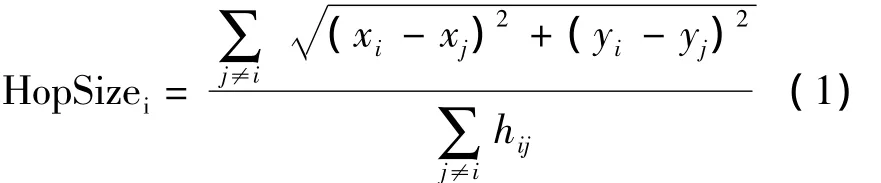
式中，(xi，yi)表示锚节点i的坐标;(xj，yj)表示锚节点j的坐标;hij表示锚节点i，j之间的最小跳数。

第3阶段利用三边定位法或极大似然估计法计算自身位置。

2 不对称链路对DV-Hop算法影响

本文以图1所示网络拓扑结构为例分析不对称链路对DV-Hop算法的影响。在图1所示网络中，部分节点间的通信链路是不对称链路，即因为设备或介质等因素影响，某些相邻节点间只能单向通信。例如10号节点能够直接接收到08号节点的数据报文，而08号节点因为不对称链路影响并不能直接接收到10号节点的数据报文。节点间的这种不对称链路导致DV-Hop第1阶段中计算的节点间跳数各不相同，从而使各锚节点计算的平均跳距存在较大误差，最终影响到整个算法的定位精度。

图1 包含不对称链路的无线传感器网络示意图

例如，13号锚节点利用式(1)计算的平均跳距为:

其中，h13，05(表示05号节点到13号节点的跳数)等于8(跳数路径为:05-06-07-02-08-10-11-14-13)，h13，19(表示19号节点到13号节点的跳数)等于6(跳数路径为:19-17-16-15-11-14-13)。

随着DV-Hop算法执行，08号节点计算自身到13号锚节点的跳数是5(最小跳数路径为:13-14-11-10-09-08)。因此，当08号节点接收到Hop-Size13，它计算得到自己距离13号锚节点的距离是5 ×HopSize13。然而，HopSize13是基于h13，05计算得到，根据h13，05可知08号节点到13号锚节点的跳数应该是4;也就是说，如果使用HopSize13作为校正值，08号节点到13号锚节点的距离应该是4×Hop-Size13;相同的情况在计算15号节点到19号锚节点和05号锚节点时也会出现，从而导致最终的三边定位出现较大误差。

由上述分析可知，若可以使得节点间的跳数计算结果与理想网络(无不对称链路)中相同，则必然可以减少这种不可预见误差，提高算法实际定位精度。

3 DV-Hop算法改进

结合上述分析，本文采用以下措施改进DV-Hop算法:①使用邻居节点挖掘措施NNM(Neighbor Nodes Mining)完成邻居节点间的准确识别;②使用最小跳数方法MHC(The Minimum Hop-Count)计算节点间的真实跳数;③采用改进的平均跳距计算方法减小测距误差;④采用一种新的方程组求解方法完成节点初步定位;⑤最后使用一种简单的坐标校准技术，进一步提高定位精度。

3.1 NNM方法

在无线传感器网络中，每个节点都会有一个邻居表NT(Neighbor Table)，理论上每个节点都应该可以直接与其邻居表中的所有节点进行通信。但是因为不对称链路的存在，节点发送出的消息可能不会被邻居表中的邻居节点直接接收。为尽量消除不对称链路对算法的影响，本文在此提出NNM方法:定义MiningMsg消息，该消息由SrcId、SrcNT、FwdId、Ttl共4个字段组成。其中SrcId表示发出信息的源节点号;SrcNT表示源节点的邻居表;FwdId表示最近一次转发过该信息的节点号;Ttl表示该消息的生存期。每个节点在约定时间段内周期性发送MiningMsg消息。对于收到该消息的节点(假设其节点号为IDtest，邻居表为NTtest)，将采用如下方法完成其邻居节点挖掘:

以图1所示无线传感器网络为例，节点08属于节点10的邻居表，而节点10并不属于节点08的邻居表。通过NNM方法，节点08可以接收到节点10的MiningMsg信息(传播路径为10-09-08)，并发现它属于节点10的邻居表，因此将节点10添加至自己的邻居表。至此，节点08和节点10完成相互之间的准确识别。

3.2 MHC方法

虽然NNM方法能够确保节点本身与其邻居表中的节点互相识别为邻居节点，但链路的不对称性是实际存在的，它会影响广播消息在网络中的传播，继而影响到节点间真实跳数的准确计算。为此，在完成邻居节点挖掘之后，为DV-Hop算法第1阶段的锚节点广播消息中添加Route［N］字段，即新的广播消息组成为{ID，xi，yi，HopCount，Route［N］}。其中Route［N］字段的每个Route元素包含{FwdId; Hops}两个变量，FwdId表示转发过该消息的节点ID，Hops表示节点FwdId与最初发出该广播消息的锚节点之间的最小跳数。

当一个节点(假设其节点号为IDtest)接收到该条广播消息，将按照下列方法完成它与相应锚节点之间的跳数计算:①HopCount字段值加1;②在Route［N］中挑出FwdId属于IDtest节点的邻居表且Hops最小的Route元素;③对于步骤②中选择的Route元素，若其Hops+1＜HopCount，则更新Hop-Count为Hops+1，然后将Route［N］中该Route元素之后的所有元素消除;④IDtest节点将HopCount作为其与锚节点之间的跳数，并将对应信息添加至该广播消息的Route［N］尾部;⑤转发更新后的广播消息。

上述方法中Route［N］字段的N取值范围推荐为2～5。在步骤④中，若Route［N］已满，则先将各元素依次前移覆盖，再将空出的第N个元素由当前节点更新。

仍然以图1为例，节点08会接收到锚节点13发出的广播消息，其中HopCount项为5(路径为13 -14-11-10-09-08)。节点08在该消息中发现:Route［3］.FwdId=10，Route［4］.FwdId=09均属于其邻居表中的节点，且Route［3］.Hops=3最小。所以，广播消息中的HopCount项更新为3+1 =4，同时把节点09对应的元素Route［4］内容从Route［N］中清除，并由节点15填充(即Route［4］. FwdId=08，Route［4］.Hops=4)后再次转发。通过这种方法，节点13和节点08计算的两者间的跳数就是相等的。

NNM和MHC方法以通信成本为代价确保了相邻节点间的准确识别，并使的节点间计算的跳数与理想环境相同，减少了跳段距离估算时的不可预见误差。

3.3 平均跳距修正

即使不考虑链路对称性问题，采用“跳段距离代替直线距离”这种做法也使DV-Hop定位算法在随机分布网络中可能产生较大的测距误差。本文在文献［3-9］的基础上对平均跳距计算进行如下改进。

3.3.1 锚节点平均跳距修正

在DV-Hop定位算法的第1阶段，基于无偏估计准则，锚节点i使用它自己算出的平均跳距值HopSizei乘以相应跳数以估计其到其它各锚节点的距离时，产生的平均误差如下式所示:

式中，N表示锚节点个数;εij表示锚节点i、j之间使用平均跳距与跳数乘积代替实际距离所引起的误差;(xi，yi)和(xj，yj)分别表示锚节点i和j的坐标; HopSizei表示锚节点i计算的平均跳距值;hij表示锚节点i、j之间的最小跳数。

对(3)而言，准确的HopSizei会使平均误差达到最小。根据最小均方误差准则，令:

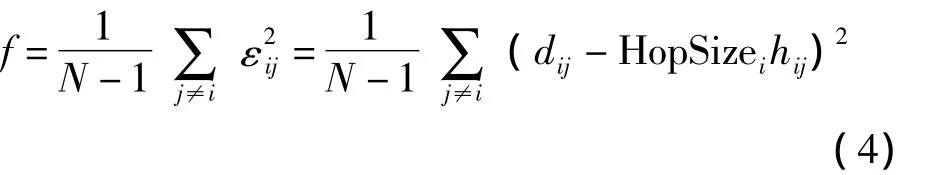
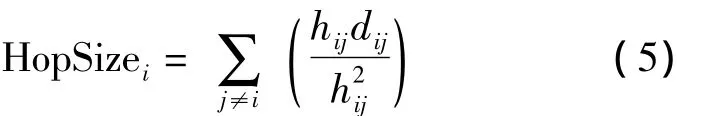
3.3.2 未知节点平均跳距修正

在传统DV-Hop定位算法中，未知节点仅记录最先收到的那个锚节点的平均跳距，并以此作为未知节点自身的平均跳距来估计它到各锚节点的估计，而参考全网所有锚节点的平均跳距信息计算未知节点的平均跳距这种极端的计算策略会极大增加网络通信成本。为了降低通信成本的同时减小平均跳距误差，在此提出一种基于局部锚节点的加权平均策略:即未知节点利用它能接收到的锚节点平均跳距信息计算其自身平均跳距，公式如(6)所示。而这些锚节点平均跳距信息由各锚节点通过带有较小生存期字段的分组广播至网络，控制在局部范围内传播，这也正是基本DV-Hop算法中校正值的扩散方式。

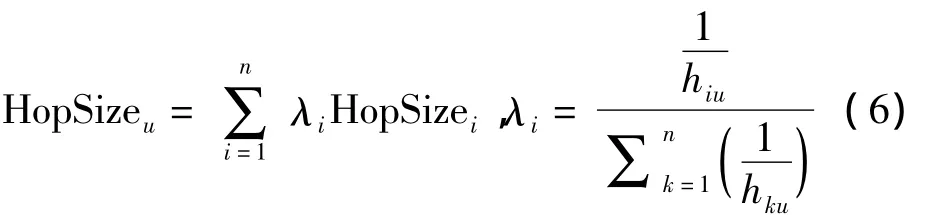
式中:hui是未知节点U和锚节点i之间的最小跳数; n是未知节点收到的锚节点平均跳距信息个数; HopSizei表示锚节点i计算的平均跳距值。

未知节点以此平均跳距乘以相应跳数计算它到各锚节点距离。

3.4 改进的方程组求解方法

传统DV-Hop算法的第3阶段是利用极大似然估计法计算节点位置。为了减少测距误差对定位算法的影响，本文采用一种改进的方程组求解方法。

假设(x，y)是未知节点u的坐标，(xi，yi)是第i (i=1，…，n)个锚节点的坐标，di是未知节点u到锚节点i的估计距离，则通过式(8)可获得未知节点u的位置估计。

式中di是带有一定测量误差的估计距离。传统DV-Hop算法中先对(7)两边平方后再去求解(x，y)，使得包含在di中的测距误差被迅速放大。在此，为了降低估计距离di中的固有误差影响，我们对(7)使用一种新的解法。

首先用方程组中的前n-1个方程分别和最后一个方程相减，则可得到如下方程组:

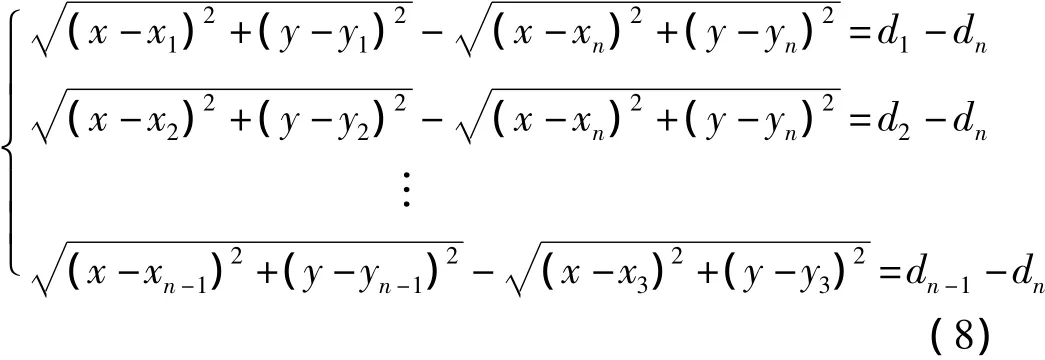
令k=x2+y2，Ai=x2i+y2i，将方程组(8)两边平方后化简可得，

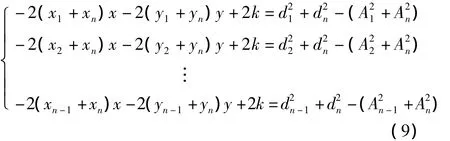
上式可用矩阵形式表示为QZ=H，其中

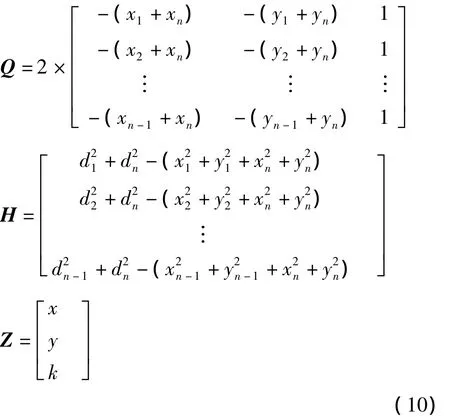
为了进一步提高定位精度，在此使用加权最小二乘方法对QZ=H求解，可得

其中，

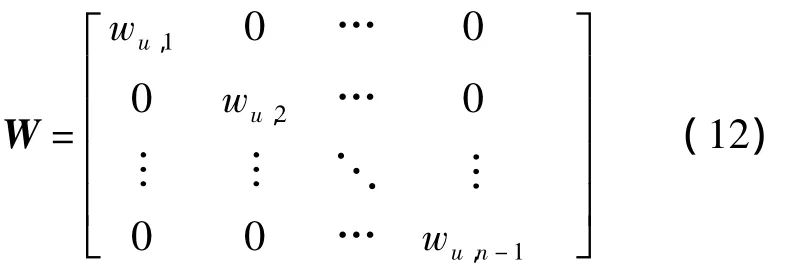
wu，i表示参考锚节点i相对于未知节点的权重，其取值为1/hui。

3.5 节点坐标校正

由上述内容可以看到，通过(11)可得未知节点的初步估计坐标(x，y)以及k的值。由于di存在测距误差，所以估计坐标(x，y)通常不满足方程组(9)的k= x2+y2。如图2所示，如果k＜x2+y2，则对于未知节点的一个更优的位置估计可能在B处;如果k＞x2+y2，对于未知节点的一个更优的位置估计可能在C处。

图2 未知节点的位置估计

所以，借助k的值可对节点坐标进行进一步校正，具体方式如下:

从(9)可知，k的表达式包含x和y。为了方便讨论，使用x'和y'分别代替k中的x和y，即k= (x')2+(y')2。令未知节点U的初步估计坐标为(x″，y″)，则有x'=t×x″，y'=t×y″。其中t是参数。因x″、y″和k的值已知，所以由k=(x')2+(y')2=(t ×x″)2+(t×y″)2即可得出t的值。

最后，使用下式修正节点坐标。

对于上式，由x'=t×x″，y'=t×y″可得

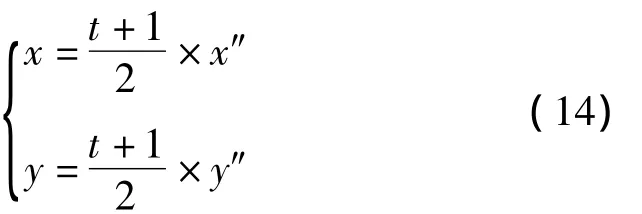
例如，假设未知节点U通过式(11)计算得到其初步估计坐标为(4，3)，k为36。则由坐标校正过程可知:x″=4，y″=3;x'=4t，y'=3t。又因k=(x')2+(y')2=36，所以t=6/5。将x″，y″和t的值带入式(14)，可得校正后的未知节点坐标估计:x=4.4，y=3.3。

4 仿真实验及性能分析

为了验证本文算法的性能，采用NS2进行仿真，并将其定位效果与基本DV-Hop算法［2］和同样针对不对称链路情况下的DV-Hop改进算法［10］相比较。所有节点坐标在网络区域(100 m×100 m)内随机生成，仿真过程中会考虑锚节点密度、网络规模等不同因素对定位误差的影响。因为本文算法试图克服复杂网络环境下存在的不对称链路对定位算法的影响，所以仿真实验会通过修改测试tcl脚本参数使网络中含有一定量的不对称链路。实验评价指标为平均定位误差，其中定位误差是定位算法输出的估计坐标与实际坐标之间的距离与节点通信半径之比;平均定位误差则是实验重复执行50次后得到的全网所有未知节点的定位误差平均值。

4.1 不同锚节点比例时的定位性能

因为锚节点的费用比普通节点高两个数量级，所以锚节点密度将直接关系到整个网络成本高低。图3显示了在不同锚节点密度时本文算法与其它两种定位算法的定位性能比较(节点总数为300，节点通信距离为15 m)。

图3 锚节点比例变化时的定位性能比较

由图3可以看到，当节点总数保持不变，而锚节点密度逐渐增大的情况下，各算法的平均定位误差都逐渐减小。这是因为锚节点密度增大使得网络中锚节点个数增多，未知节点可以获得更多的高精度位置参考信息，它到各锚节点的距离估计更加接近实际距离。其中本文定位算法定位效果最好，其定位误差比基本DV-Hop算法平均减小约16%，比文献［10］中的改进算法平均减小约12%。这主要得益于本文算法所采取的邻居节点挖掘机制和最小跳数计算方法能有效抑制或避免不对称链路的影响，而平均跳距修正、新的方程组求解方法和最后的坐标校正技术更是进一步提高了节点定位精度。从图3还可以看到，本文算法只需较少量的锚节点即可得到一个较好的定位效果，比其它两种算法更能有效减少锚节点需求，降低网络成本。

4.2 不同节点规模时的定位性能

图4显示了在不同节点规模时3种算法的定位效果(锚节点比例为10%，节点通信半径为15m)。由图4可见，各算法的平均定位误差均随着节点总数的提高而逐渐降低。其中本文定位算法定位效果仍然最好，其定位误差比基本的DV-Hop算法平均减小约15%，比文献［10］的算法平均减小约12%。从图4还可以看到，网络越是稀疏，本文算法的定位效果越突出，比如当网络中的节点总数为200时，本文算法与其它两种算法相比，其定位误差分别降低了16%和15%。这同样得益于本文算法的邻居节点挖掘机制、最小跳数计算方法及后期的改进和坐标校正。可见，在相同的监测区域和锚节点比例下，本文算法对传感器节点的需求更少，更节约网络成本。

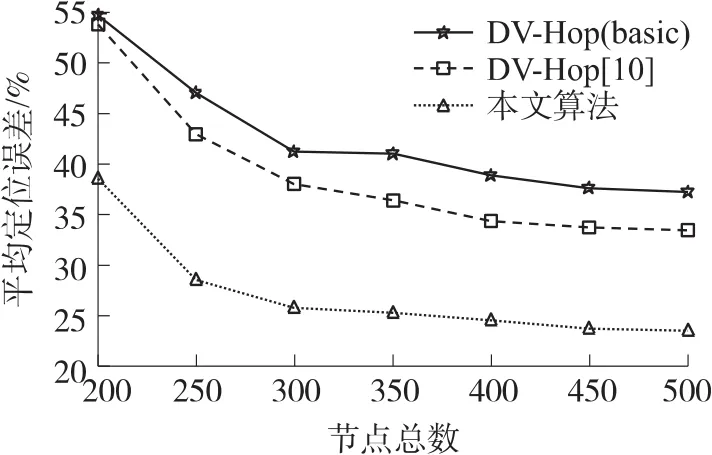
图4 节点总数变化时的定位性能比较

4.3 不同网络连通度时的定位性能

网络连通度体现了网络中单个节点通信范围内的平均节点数目。为降低网络成本，在保证定位性能的前提下，网络连通度应越小越好。图5给出了不同网络连通度时3种算法的定位效果。

图5 网络连通度变化时的定位性能比较

由图5可见，随着网络连通度增大，各算法的平均误差均逐渐减小。在相同的网络连通度下，本文算法的定位效果最好。其定位误差比基本DV-Hop算法平均降低约15%，比文献［10］的改进算法平均降低约12%。定位误差的降低再次验证了本文邻居节点挖掘机制、最小跳数计算方法及坐标校正等改进措施的有效性。从图5还可以看到，只需要较小的网络连通度，本文算法即可达到较好的定位效果。这进一步体现了本文算法在节约网络成本方面的优势。

5 通信成本及计算时间

定位算法的通信成本通常由定位过程中传输的消息分组个数表示。与传统DV-Hop算法相比，本文算法的邻居挖掘机制和最小跳数计算方法都是以通信成本为代价换取定位精度的提升，对此，我们认为这是值得的，特别是当网络环境复杂导致有大量不对称链路存在时，本文算法的优势将更加明显。

另外，本文算法的邻居挖掘机制、最小跳数计算方法和后期的坐标校正将会增加节点的定位计算时间。图6显示了上述3种定位算法在不同网络规模时的定位时间比较。可以看到，本文算法与文献［10］所述算法需要的定位时间接近，比传统DVHop算法增加了约0.12 s，对此，我们认为定位时间和上文所述通信成本的增加都是必要的，这些付出将会带来复杂环境下算法定位精度的大幅度提升。

图6 节点总数变化时的定位时间比较

6 结束语

节点定位是无线传感器网络的关键技术。现有

DV-Hop算法很容易受不对称链路的影响而产生较大的定位误差。本文为此提出一种改进算法。新算法首先使用邻居节点挖掘措施和最小跳数计算方法确保相邻节点的准确识别以及节点间的跳数的准确计算;接着使用改进的平均跳距计算方法减小平均跳距误差;然后采用一种新的方程组求解方法完成节点初步定位;最后使用一种坐标校正技术进一步提高定位精度。仿真结果显示，本文算法以适当的通信成本和计算开销为代价，在明显提高定位精度的同时有效降低了网络成本，能适应于多种应用环境。

［1］Boukerche A，Oliveira H A B F，Nakamura E F，et al.Localization Systems for Wireless Sensor Networks［J］.IEEE Wireless Communications，2007，14(6):6-12.

［2］Niculescu D，Nath B.Ad Hoc Positioning System(APS)［C］// Proceeding of the 2001 IEEE Global Telecommunications Conf，San Antonio:IEEE Communications Society，2001:2926-2931.

［3］林金朝，陈晓冰，刘海波.基于平均跳距修正的无线传感器网络节点迭代定位算法［J］.通信学报，2009，30(10):107-113.

［4］江禹生，冯砚毫.一种新的DV-Hop定位算法［J］.传感技术学报，2010，23(12):1815-1819.

［5］Qian Q，Shen X，Chen H.An Improved Node Localization Algorithm Based on DV-Hop for Wireless Sensor Networks［J］.Computer Science and Information Systems，2011，8(4):953-972.

［6］张震，闫连山，刘江涛，等.基于DV-hop的无线传感器网络定位算法研究［J］.传感技术学报，2011，24(10):1469-1472.

［7］Kumar S，Lobiyal D K.An Advanced DV-Hop Localization Algorithm for Wireless Sensor Networks［J］.Wireless Personal Communications，2013，71(2):1365-1385.

［8］石为人，贾传江，梁焕焕.一种改进的无线传感器网络DV-Hop定位算法［J］.传感技术学报，2011，24(1):83-87.

［9］Chen X，Zhang B.Improved DV-Hop Node Localization Algorithm in Wireless Sensor Networks［J］.International Journal of Distributed Sensor Networks，2012，2012:1-7.

［10］Zhao H G，Shi H S，Zhao Y H.Range-Free Localization Algorithm in Wireless Sensor Networks with Asymmetric Links［J］.Applied Mechanics and Materials，2014，446:1591-1595.

［11］Zhao J，Govindan R，Estrin D.Computing Aggregates for Monitoring Wireless Sensor Networks［C］//Proceedings of the First IEEE International Workshop on Sensor Network Protocols and Applications，2003:139-148.

［12］Zhou G，He T，Krishnamurthy S，et al.Impact of Radio Irregularity on Wireless Sensor Networks［C］//Proceedings of the 2nd International Conference on Mobile Systems，Applications，and Services，New York: ACM，2004:125-138.

［13］Zhao J，Govindan R.Understanding Packet Delivery Performance in Dense Wireless Sensor Networks［C］//Proceedings of the 1st International Conference on Embedded Networked Sensor Systems，New York:ACM，2003:1-13.

张亚明(1980-)，男，汉族，博士生，研究方向为无线传感器网络，zhangym333@ 163.com;

史浩山(1946-)，男，汉族，西北工业大学教授、博士生导师，研究方向为无线通信、计算机通信网络、无线传感器网络，shilaoshi@nwpu.edu.cn。

不对称链路环境下的WSN节点定位算法*

张亚明1，史浩山1*，刘燕2，程伟1
(1.西北工业大学电子信息学院，西安710072;2.西安电子科技大学天线与微波技术重点实验室，西安710071)

针对无需测距定位算法DV-Hop在含有不对称链路的复杂环境中存在较大定位误差的问题，从5个方面对其进行了改进:首先采用邻居节点挖掘措施确保相邻节点的准确识别;接着使用最小跳数方法计算未知节点到锚节点之间的真实跳数;然后使用改进的平均跳距计算方法减小平均跳距误差;其次采用一种新的方程组求解方法完成节点初步定位;最后采用一种校正技术对初步估计坐标进行校准。仿真结果表明，改进算法以适当增加通信成本和计算开销为代价，有效避免了不对称链路的影响，在明显提高定位精度的同时降低了网络成本。

无线传感器网络;定位;DV-Hop算法;不对称链路

TP393

A

1004－1699(2014)03－0320－07

2014-01-07修改日期:2014-03-11

C:6150P;7230

10.3969/j.issn.1004－1699.2014.03.009

项目来源:国家自然科学基金项目(61301092，61202314);陕西省自然科学基金项目(2012JQ8005)