声子晶体串联组合杆振动带隙研究

舒海生，高恩武，刘少刚，赵 丹，王威远

(哈尔滨工程大学 机电工程学院702所，哈尔滨 150001)

受天然晶体电子能带理论启发，已有对周期复合材料或结构中经典波传播的研究[1]。弹性波在弹性常数、材料密度、结构尺寸等参数周期性调制下传播时会产生声子带隙，即一定频带范围内弹性波传播受到抑制或禁止。因此声子晶体或理论上或减振降噪，对精密机械减振平台、新型滤波器等工程应用领域均具有重要价值。声子晶体研究主要集中在带隙形成机理分析及带隙计算方法探索等[2-7]，实际应用研究[8]较少。研究对象多为单一构型声子晶体，如一维声子晶体中梁、杆、轴[2,9]及二维声子晶体[3,10]中格栅、板等，而对实际应用中组合形式结构件研究较少。对声声子晶体平面组合杆情况，如T型杆[10]、角梁等在结合处能实现波形转换，拓宽带隙频率范围，且已取得二维宽频较好减振效果。而工程实际中激扰多为三维，需研究三维宽频减振元件。为此，本文将声子晶体理念引入串联型空间组合杆结构构造声子晶体串联组合杆，综合利用弯曲、纵向、扭转带隙，达到多维宽频减振效果。具体步骤为：①对声子晶体串联组合杆振动特性进行理论分析，推导总传递矩阵；②据总传递矩阵编写MATLAB程序进行数值计算，重点研究加载方向及杆件间夹角对声子晶体串联组合杆振动特性影响；③用有限元方法分析振动传递特性，证明理论分析的正确性；④用遗传算法对影响减振性能因素的杆件间夹角进行最优化设计；⑤给出结论。

1 声子晶体串联组合杆理论分析

图1为声子晶体串联组合杆一般结构(以3杆为例，对K(K≥3)杆情况分析过程相同)，上(杆Ⅲ)、中(杆Ⅱ)、下(杆Ⅰ)材料分布及周期结构尺寸相同，杆Ⅰ、Ⅱ组成的面称为面Ⅰ，杆Ⅱ、Ⅲ组成的面为面Ⅱ。为研究方便，规定杆Ⅰ与Ⅱ、Ⅲ分别位于面Ⅰ、面Ⅱ内。杆Ⅰ与Ⅱ，杆Ⅱ与Ⅲ，面Ⅰ与Ⅱ间夹角分别为θ1,θ2,θ3，杆与杆间固结。声子晶体串联组合杆振动可解耦为组合杆面内振动及垂直于组合杆平面的面外振动。面内振动分面内弯曲振动、纵向振动，面外振动分面外弯曲振动、扭转振动。由于声子晶体串联组合杆为空间立体结构，在杆Ⅰ与Ⅱ、杆Ⅱ与Ⅲ结合处组合杆存在面内振动与面外振动相互转化情况，总体上表现出弯振、纵振、扭振的全耦合特性。

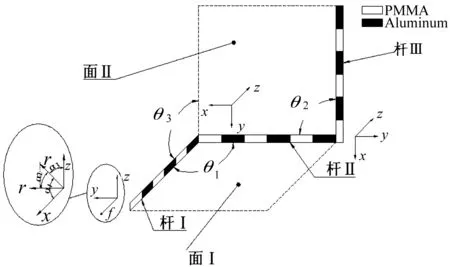
图1 声子晶体串联组合杆模型

当面内振动的弯曲波或纵波在单独杆Ⅰ、Ⅱ或Ⅲ中传播时，不同周期间传递关系[10]可写为

(1)

(2)

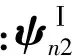
当面外振动弯曲波或扭转波在单独杆Ⅰ、杆Ⅱ或杆Ⅲ中传播时，不同周期间传递关系[10]可写为

(3)

(4)

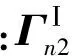
为便于叙述，将同周期同材料面内振动解系数列阵与面外振动解系数列阵组合为

(5)

(6)

据式(1)～式(6)得：

(7)

(8)

图1表明，杆Ⅰ在杆Ⅰ与杆Ⅱ结合处为第n周期，而杆Ⅱ在结合处为第1周期。据杆Ⅰ、杆Ⅱ结合处位移、弯曲角、扭转角、弯矩、扭矩、剪力、正应力等协调条件，有

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

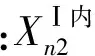
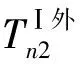
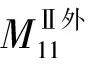
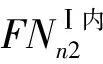
将式(9)～(20)写成矩阵形式为

(21)

据杆Ⅱ、杆Ⅲ结合处位移、弯曲角、扭转角、弯矩、扭矩、剪力、正应力等协调条件，有：

(22)

(23)

(24)

(25)

(26)

(27)

(28)

(29)

(30)

(31)

(32)

(33)

式中：字符号含义同上。

将式(22)～式(33)写成矩阵形式为

(34)

声子晶体串联组合杆(3杆)总传递矩阵写为

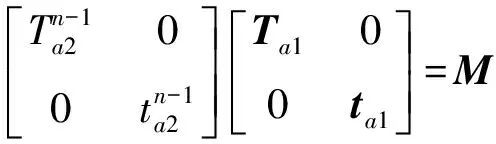
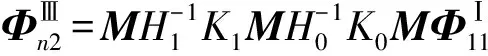
一般的声子晶体串联组合杆(K根杆)总体传递矩阵可写为

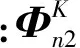
2 声子晶体串联组合杆数值分析

2.1 声子晶体单杆数值分析

便于对比，利用传递矩阵法对3周期声子晶体单杆进行数值分析。基本参数设置为：各子段直径D=5 mm，长a1=50 mm；铝的弹性模量E1=7.21×1010Pa，质量密度ρ1=2 799 kg/m3，泊松比ν1=0.345 1；有机玻璃弹性模量E2=0.32×1010Pa，质量密度ρ2=1 062 kg/m3，泊松比ν2=0.333 3。单杆纵向、弯曲及扭转振动传递率计算结果见图2。由图2看出，在0～8 kHz范围内存在明显纵向振动带隙5 900～8 000 Hz；两明显弯曲振动带隙为1 420～2 680 Hz，3 920～5 720 Hz；扭转振动带隙为3 600～8 000 Hz。单杆在三种不同形式下振动带隙重叠部分较小，只能获得二维减振效果，故需研究能综合运用三种振动带隙的结构，实现三维减振目的。

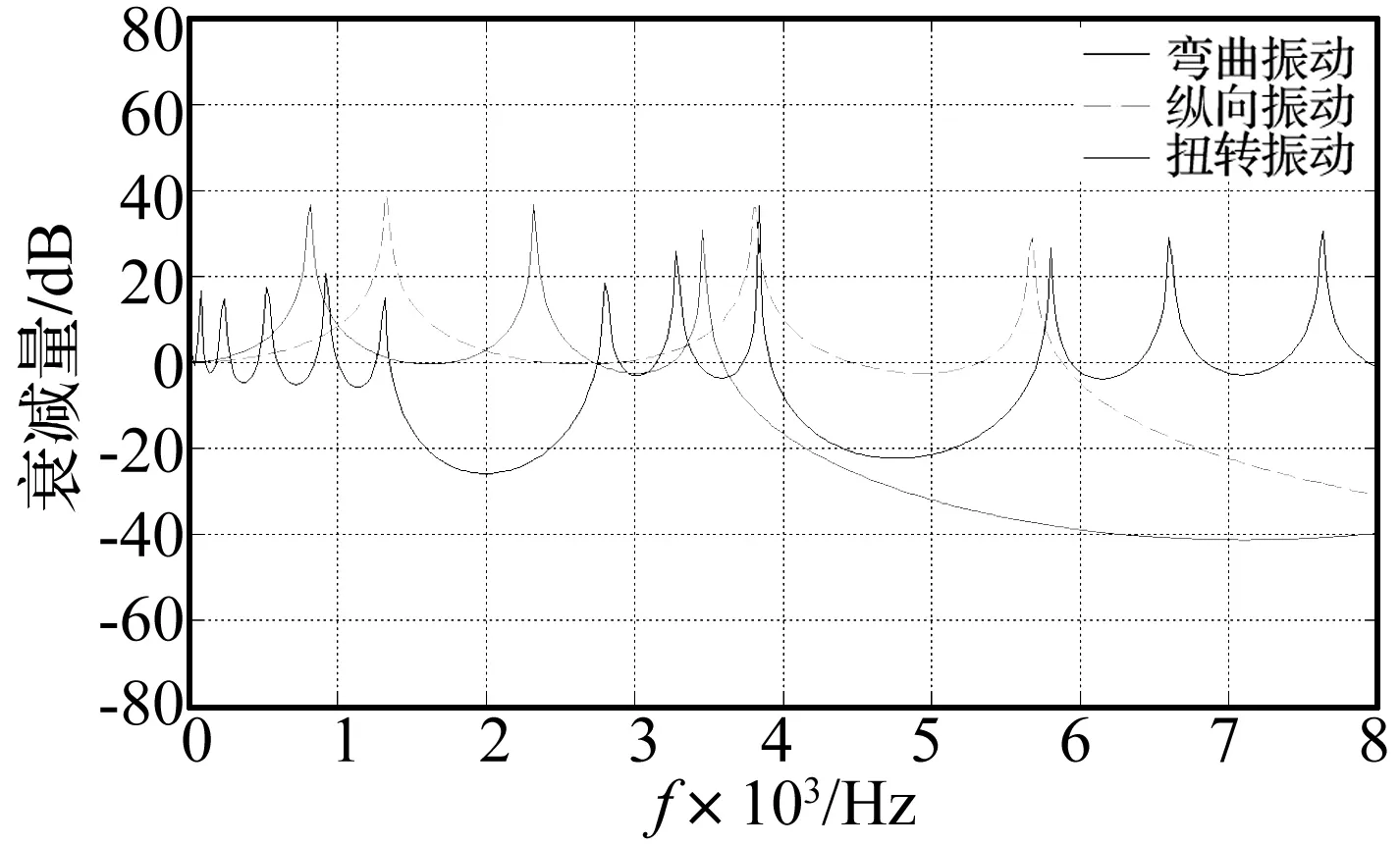
图2 声子晶体单杆弯曲、纵向及扭转振动传递率曲线

2.2 声子晶体串联组合杆振动特性研究

据传递矩阵法推导结果，利用MATLAB数值计算，由加载方向及杆件间夹角两方面研究3周期单杆组成的串联组合杆(三杆)结构振动特性。基本参数设置同声子晶体单杆。

2.2.1 加载角对振动特性影响

工程中激励负载大多为多维，为更好模拟外部各种激扰对杆件同时作用情况，引入加载向量r，方向余弦为cosα1，cosα2，cosα3。激扰在3坐标平面加载见图3。

图3 加载方向

针对加载方向余弦(cosα1，0，cos(90°-α1)),(α1从0°逐渐增到90°，步长30°)情况，数值计算结果见图4(a)。由图4(a)看出，α1逐渐增大时在第一弯曲带隙范围(1 420～2 680 Hz)内衰减量逐渐增大，纵向带隙范围(7 100～8 000 Hz)内衰减量逐渐减小，第二弯曲带隙变化规律不明显，但总体能反映组合杆由纵向振动占主导地位逐渐转变为弯曲振动占主导地位；弯曲带隙作用越明显，位于纵向带隙中弯曲波传输共振峰影响(6 600，7 640 Hz附近，图3)亦越显著，导致α1趋于90°时峰附近衰减效果明显削弱； 而α1较小时情况

相反，纵向振动逐渐占据主导地位，纵向带隙衰减作用得以更好体现，衰减显著，弯曲带隙内衰减有所减弱；位于弯曲带隙中纵波传输共振峰(5 660 Hz附近，图3)影响加强，导致此峰值附近减振效果明显减弱。因此，该结构能获得较好的二维宽频减振性能。考虑加载方向余弦(cos(90°-α2), cosα2,0)(α2从0°逐渐增到90°,步长30°)结果见图4(b)。由图4(b)看出，加载角逐渐增大时第一弯曲带隙范围内衰减量逐渐减小，第二弯曲带隙范围(1 400～2 400 Hz)内情况较复杂，规律不明显，纵向带隙范围内衰减量逐渐增大，总体有组合杆由弯曲振动占主导地位向纵向振动占主导地位转变趋势。

考虑加载方向余弦(0,cos(90°-α3),cosα3)(α3从0°逐渐增到90°,步长30°)时仿真结果见图4(c)。由图4(c)看出，面内、外加载对整个声子晶体组合杆减振频带范围影响不同：第一弯曲带隙1 400～2 120 Hz、第二弯曲带隙4 360～5 000 Hz范围内，随加载角逐渐增大减振幅值增大，而第一弯曲带2 120～2 600 Hz、第二弯曲带隙3 800～4 360 Hz范围内，随加载角逐渐增大减振效果减弱。故在1 400～2 120 Hz、4 360～5 000 Hz频带范围内面内弯曲振动占主导地位，在2 120～2 600 Hz、3 800～4 360 Hz范围内面外弯曲振动占主导地位。低频段0～1 000 Hz内声子晶体串联组合杆表现出一定减振性能，由于该频带不在声子晶体杆或梁的带隙内，因而该减振能力已不能用带隙解释。事实上此频段内无论弯曲波或纵波波长均远大于杆Ⅰ特征尺寸，因此该弯曲波、纵波在杆中的传播类似于杆或梁的整体运动，即纯刚体运动，此时杆Ⅱ、Ⅲ可视为悬臂梁，与杆Ⅰ形成传统隔振系统中“悬臂梁-振子”体系，产生相似的隔振效果。由于“悬臂梁-振子”隔振体系固有的不足，在该频段内存在较多共振峰。在杆件结合处存在波形转换，其它频带范围内也出现共振峰，可通过增加阻尼等方法进行削减。

(a) 加载方向余弦(cosα1，0 ，cos(90°-α1))声子晶体串联组合杆传递率曲线(b) 加载方向余弦(cos(90°-α2)，cosα2，0)声子晶体串联组合杆传递率曲线(c) 加载方向余弦(0，cos(90°-α3), cosα3)声子晶体串联组合杆传递率曲线

总之，无论采用何种角度加载，除局部共振峰不利影响外，整个面内、外振动带隙范围内均能产生较强减振效果，此表明该声子晶体串联组合杆可实现空间内三维宽频减振目的。由于“悬臂梁-振子”效应，低频范围内随加载角的变化也有一定减振效果，如加载方向余弦(0,0,1)时，在920～1 200 Hz范围内能形成达-28 dB的减振衰减区域。

比较图4发现，加载角从0°～90°变化时，对应的传递率曲线族基本介于0°与90°两条传递率曲线之间，因此可将该两条传递率曲线作为包络线进行重点研究；加载角为0°或90°时衰减量最显著，故应用中选加载角时应据振源特点尽量用0°或90°方向角。

2.2.2 杆件夹角对振动传递特性影响

为进一步了解声子晶体串联组合杆减振性能，对声子晶体杆间不同夹角β1，β2，β3(β1为杆Ⅰ与杆Ⅱ间夹角，β2为杆Ⅱ与杆Ⅲ间夹角，β3为杆Ⅲ、杆Ⅰ、杆Ⅱ组成的面夹角)进行分析。加载方向余弦为(0,0,1)时β1-90°-90°(β1由30°～90°，步长30°)振动传递率曲线对比见图5(a)，加载方向余弦为(0,0,1)时90°-β2-90°振动传递率曲线对比见图5(b)，加载角为(0,0,1)时90°-90°-β3振动传递率曲线对比见图5(c)。通过比较不难发现，β1对高频范围(7 200～8 000 Hz)有较大影响(图5(a))，随β1增大衰减量逐渐增大；β2对中低频范围(1 420～2 680 Hz)作用明显，(图5(b))，β2为90°时减振效果明显优于其它两种；β3主要影响中高频范围(3 940～5 200 Hz)，随β3增大衰减量逐渐减小。对其它加载方向余弦如(1,0,0)，(0,1,0)结论类似。由于夹角对减振性能有显著影响，实际应用中组合杆夹角选择尤其重要，以组合杆结构为例，隔振频率在较高的7 200～ 8 000 Hz范围内时，β1应选90°夹角；隔振频率为中高频率3 940～5 200 Hz范围内时，β3应设计的小点；隔振频率在中低频率1 420～2 680 Hz范围内时，β2则应选90°夹角。总之，声子晶体组合杆的减振性能为β1，β2，β3综合作用结果，应针对不同减振需求，对杆件夹角进行优化设计。

(a) 杆件夹角为β1-90°-90°声子晶体串联组合杆传递率曲线(b) 杆件夹角为90°-β2-90°声子晶体串联组合杆传递率曲线(c) 杆件夹角为90°-90°-β3声子晶体串联组合杆传递率曲线

3 声子晶体串联组合杆有限元分析

为验证理论分析的正确性，进行声子晶体串联组合杆有限元仿真。重点研究杆件间夹角为90°情况，基本设置为：① 材料参数：连接块密度4 000 kg/m-3，弹性模量2E11Pa ，泊松比0.3，其余材料参数同数值计算。② 网格划分：用自由网格划分，单元类型SOLID186，杆节点数17 010，单元数3 056。③加载：简谐位移激励幅值0.001 m。④ 分析设置：用谐响应分析及用Full算法。

加载角方向余弦为(1,0,0)、(0,1,0)、(0,0,1)的有限元仿真及理论分析对比结果见图6，其中实线为理论分析结果，虚线为有限元仿真结果。由图6看出，三种加载的理论分析与有限元分析传递率曲线走势基本相同，即：加载方向为(1,0,0)时，在1 400～2 600 Hz、4 000～5 000 Hz及6 100～8 000 Hz范围内理论分析与有限元结果均出现较大振动衰减量(图6(a))；加载方向为(0,1,0)时，在1 400～2 800 Hz及 4 000～5 600 Hz范围内理论分析与有限元仿真传递率曲线较吻合(图6(b))；加载方向为(0,0,1)时，在1 420～ 及3 941～5 201 Hz范围内理论分析与有限元分析传递率曲线吻合较好(图6(c))。虽理论分析结果基本符合有限元结果，但仍存在一定误差，其主要原因为计算模型与仿真模型有误差，有限元仿真模型杆件间通过连接块连接，而计算模型则视杆件连接处为质点。声子晶体组合杆仿真结果已有力验证理论分析的正确性，且减振性能良好。

(a) 加载方向余弦(1,0,0)声子晶体串联组合杆传递率曲线(b) 加载方向余弦(1,0,0)声子晶体串联组合杆传递率曲线(c) 加载方向余弦(0,0,1)声子晶体串联组合杆传递率曲线

4 杆件夹角最优化

由以上分析知，声子晶体组合杆振动特性受多因素(如β1，β2，β3)综合影响。声子晶体研究大多针对正问题，即已知声子晶体结构、材料求带隙特性，而工程中更需据所需振动特性如带隙位置设计合理的声子晶体结构，即声子晶体反问题。在理论分析基础上将遗传算法引入声子晶体组合杆结构设计，对杆件夹角参数进行优化，筛选符合要求的最优结构。设所需减振范围1 500～2 500 Hz，设计变量为β1，β2，β3，建立优化模型。目标函数为

式中：DB(β1,β2,β3)为组合杆减振幅值。由于遗传算法要求目标函数必须为正值，故将每组减振幅值增加100 dB作为补偿，取1 500～2 500 Hz范围内均值作为目标函数。

约束取π/6≤β1,β2,β3≤π/2。遗传算法具体参数设置为每一代个体数NIND =40，最大遗传代数MAXGEN=200，代沟GGAP= 0.9。采用二进制编码，编码位数20。运算采用随机遍历抽样算子，交叉运算采用两点交叉算子，变异运算采用离散变异算子。通过遗传算法求解获得目标函数收敛曲线见图7。由图7看出，经200代优化获得结果为β1=30°，β2=89.63°，β3=83.48°。在中低频范围1 500～2 500 Hz内，夹角β2对振动特性影响较大，β2=90°时减振效果较好。通过遗传算法优化结果β2=89.63°，与结论基本一致。将几种未优选的声子组合杆与优化后声子晶体组合杆传递率曲线对比见图8。由图8看出，优化后声子晶体组合杆减振性能整体优于其它情况，尤其在1 500～1 700 Hz范围内减振效果加明显。不同组合杆形式在1 500～2 500 Hz范围内平均减振幅值即综合减振性能见图9，幅值越小表示综合减振性能越好。由图9看出，优选的组合杆形式综合减振性能最好。由于影响声子晶体组合杆减振性能因素较多，如杆径比(子段A、B直径比)、子杆长度比、弹性模量等，通过遗传算法优化多参数目标函数，选出减振性能最优的声子晶体组合杆形式为研究重点。

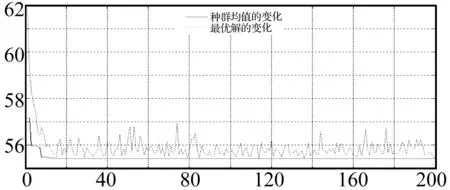
图7 目标函数收敛曲线

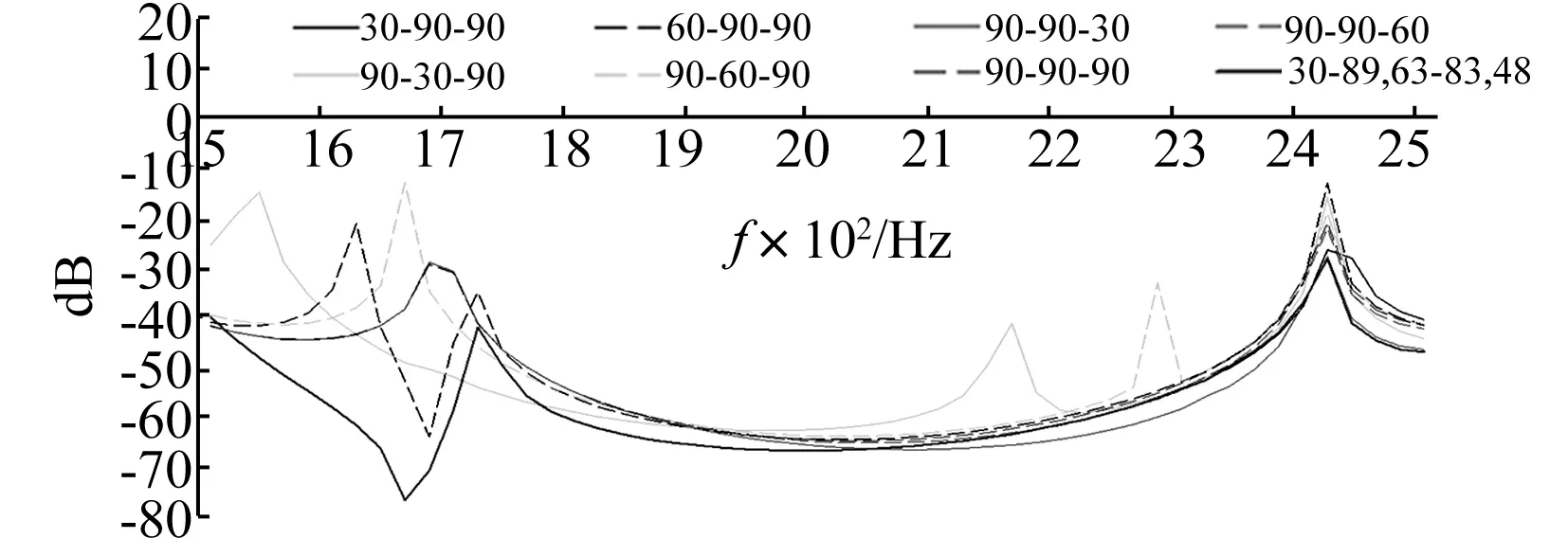
图8 声子晶体组合杆传递率对比

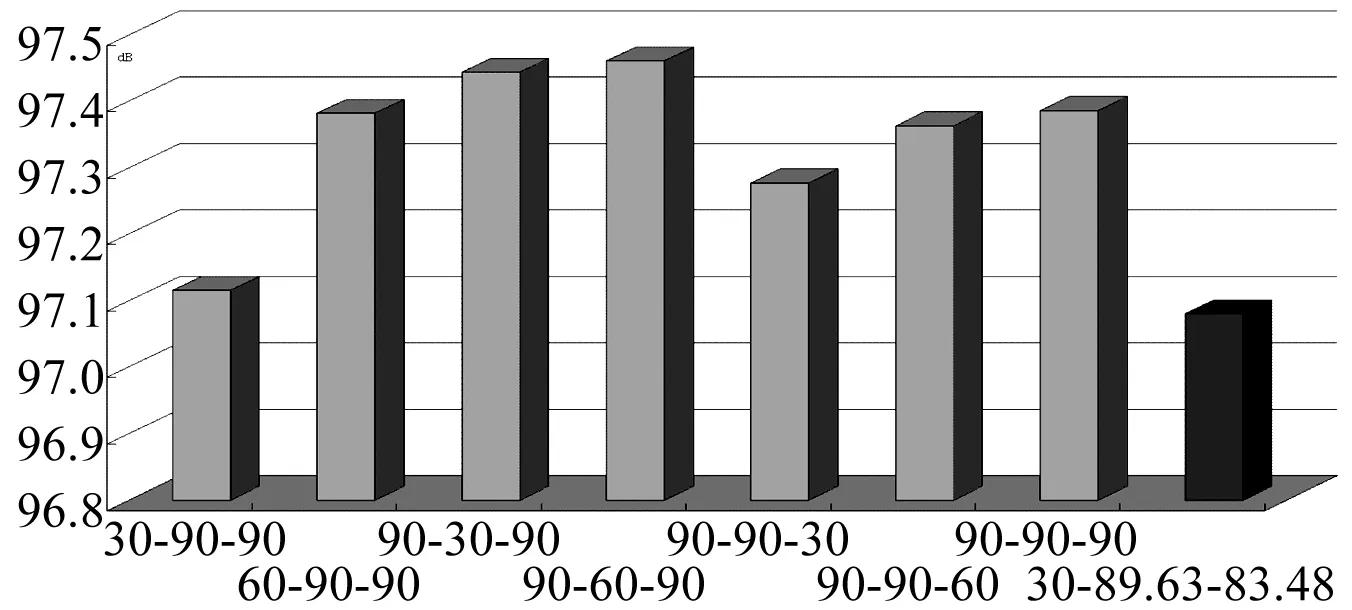
图9 声子晶体组合杆目标函数值对比

5 结 论

用传递矩阵法计算声子晶体串联组合杆振动带隙，并用数值计算与有限元仿真对振动传递特性进行计算及分析，结论如下：

(1) 声子晶体串联组合杆具有三维宽频减振能力，为良好的宽频多维减振元件。其机理在于声子晶体串联组合杆可实现波型转换，使弯曲、纵向、扭转带隙同时发挥作用，达到多维宽频减振效果。

(2) 加载角对声子晶体串联组合杆减振性能有一定影响。应据振源频率特点尽量选用0°或90°加载角。

(3) 杆件间夹角对减振性能影响明显。实际应用中应综合考虑各杆件间夹角，进行夹角最优化求解，确定最佳角度以满足不同减振需求。

[1] 温熙森,温激鸿,郁殿龙,等。声子晶体[M].北京：国防工业出版社，2009.

[2] 宋卓斐，王自东，王艳林，等。一维杆状声子晶体的带隙特性[J].振动与冲击，2010，29(2)：145-148.

SONG Zhuo-fei, WANG Zi-dong, WANG Yan-lin, et al. The characteristic of stop-band of a kind PC rod [J]. Journal of Vibration and Shock,2010,29(2):145-148.

[3] Goffaux C, Sanchez-Dehesa J. Two-dimensional phonon crystals studied using a variational method: application to lattices of locally resonant materials[J]. Physical Review B,2003, 67(14):144301-144301.

[4] Psarobas I E, Sigalas M M. Elastic band gaps in a fcc lattice of mercury spheres in aluminum[J]. Physical Review B,2002, 66(5):052302-052302.

[5] Liu Z Y, Chan C T, Sheng P. Analytic model of phononic crystals with local resonances[J]. Physical Review B,2005, 71(1):014103-014103.

[6] Lai Yun, Zhang Zhao-Qing. Large band gaps in elastic phononic crystals with air inclusions[J]. Applied Physics Letters, 2003,83(19):3900-3902.

[7] Martinsson P G, Movchan A B.Vibrations of lattice structures and phononic band gaps[J]. Q.J. Mech. Appl. Math., 2003,56:45-64.

[8] 郁殿龙,温激鸿,刘耀宗.充液周期管路的轴向振动带隙特性[J].机械工程学报,2009, 45(9):36-41.

YU Dian-long, WEN Ji-hong, LIU Yao-zong. Axial vibration property of periodic pipe system conveying fluid[J]. Journal of Mechanical Engineering,2009,45(9): 36-41.

[9] Wang Gang, Wen Xi-sen, Wen Ji-hong,et al. Quasi one-dimensional periodic structure with locally resonant band gap[J].ASME Journal of Applied Mechanics, 2006,73(1): 167-169.

[10] Shu Hai-sheng,Liu Shao-gang,Zhao Dan,et al. A combined sonic crystal rod of Bragg type with ability of vibration reduction in broad frequency band[J]. Noise Control Engineering Journal,2012,60(1): 42-61.